名校
1 . 已知函数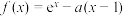 ,其中
,其中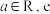 为自然对数底数.
为自然对数底数.
(1)讨论函数 的单调性,并写出相应的单调区间;
的单调性,并写出相应的单调区间;
(2)已知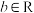 ,若函数
,若函数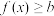 对任意
对任意 都成立,求
都成立,求 的最大值.
的最大值.
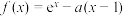 ,其中
,其中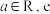 为自然对数底数.
为自然对数底数.(1)讨论函数
 的单调性,并写出相应的单调区间;
的单调性,并写出相应的单调区间;(2)已知
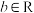 ,若函数
,若函数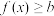 对任意
对任意 都成立,求
都成立,求 的最大值.
的最大值.
您最近一年使用:0次
2021-08-10更新
|
266次组卷
|
6卷引用:福建省德化一中、永安一中、漳平一中2018届高三上学期三校联考数学(文)试题1
福建省德化一中、永安一中、漳平一中2018届高三上学期三校联考数学(文)试题1福建省德化一中、永安一中、漳平一中2018届高三上学期三校联考数学(文)试题22016届河北省衡水中学高三二调理科数学试卷(已下线)2017-2018学年第一学期期末复习备考之精准复习模拟题高二年级(文)人教版数学试题(B卷)江苏省无锡市宜兴市张渚高级中学2020-2021学年高二下学期3月月考数学试题四川省成都市简阳市阳安中学2022-2023学年高二下学期期中考试数学(文)试题
2 . 如图,在平面直角坐标系xOy中, 已知圆O:x2+y2=4,椭圆C: +y2=1,A为椭圆右顶点.过原点O且异于坐标轴的直线与椭圆C交于B,C两点,直线AB与圆O的另一交点为P,直线PD与圆O的另一交点为Q,其中D(-
+y2=1,A为椭圆右顶点.过原点O且异于坐标轴的直线与椭圆C交于B,C两点,直线AB与圆O的另一交点为P,直线PD与圆O的另一交点为Q,其中D(-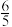 ,0).设直线AB,AC的斜率分别为k1,k2.
,0).设直线AB,AC的斜率分别为k1,k2.
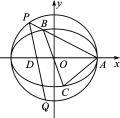
(1) 求k1k2的值;
(2) 记直线PQ,BC的斜率分别为kPQ,kBC,是否存在常数λ,使得kPQ=λkBC?若存在,求λ的值;若不存在,说明理由;
(3) 求证:直线AC必过点Q.
 +y2=1,A为椭圆右顶点.过原点O且异于坐标轴的直线与椭圆C交于B,C两点,直线AB与圆O的另一交点为P,直线PD与圆O的另一交点为Q,其中D(-
+y2=1,A为椭圆右顶点.过原点O且异于坐标轴的直线与椭圆C交于B,C两点,直线AB与圆O的另一交点为P,直线PD与圆O的另一交点为Q,其中D(-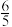 ,0).设直线AB,AC的斜率分别为k1,k2.
,0).设直线AB,AC的斜率分别为k1,k2.
(1) 求k1k2的值;
(2) 记直线PQ,BC的斜率分别为kPQ,kBC,是否存在常数λ,使得kPQ=λkBC?若存在,求λ的值;若不存在,说明理由;
(3) 求证:直线AC必过点Q.
您最近一年使用:0次
2020-01-18更新
|
631次组卷
|
11卷引用:福建省莆田第九中学2018届高三上学期期中考试数学(理)试题
福建省莆田第九中学2018届高三上学期期中考试数学(理)试题2016届江苏省泰州市高三第一次模拟考试理科数学试卷2016届江苏省清江中学高三下学期周练数学试卷12016届黑龙江大庆实验中学高三考前训练一文科数学试卷2016届黑龙江大庆实验中学高三考前训练一理科数学试卷四川省广元市高2018届高三第二次高考适应性统考文科数学试题四川省广元市2018届高三第二次高考适应性统考理科数学试题(已下线)专题12 圆锥曲线的综合应用-《巅峰冲刺2020年高考之二轮专项提升》(江苏)(已下线)专题45 盘点圆锥曲线中的定点问题——备战2022年高考数学二轮复习常考点专题突破四川省泸州高级中学校2022届高三五月月考数学(理)试题【全国百强校】黑龙江省哈尔滨市第六中学2017-2018学年高二下学期期末考试数学(理)试题
名校
3 . 已知函数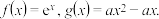 ,若曲线
,若曲线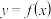 上存在两点,这两点关于直线
上存在两点,这两点关于直线 的对称点都在曲线
的对称点都在曲线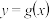 上,则实数
上,则实数 的取值范围是
的取值范围是
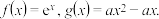 ,若曲线
,若曲线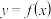 上存在两点,这两点关于直线
上存在两点,这两点关于直线 的对称点都在曲线
的对称点都在曲线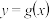 上,则实数
上,则实数 的取值范围是
的取值范围是A.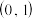 | B. | C. | D.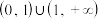 |
您最近一年使用:0次
2017-06-11更新
|
2021次组卷
|
4卷引用:福建省泉州市2017届高三(5月)第二次质量检查数学(理)试题
福建省泉州市2017届高三(5月)第二次质量检查数学(理)试题(已下线)专题2-1 函数性质及其应用(讲+练)-3广东省汕头市金山中学2024届高三上学期第一次模拟考试数学试题辽宁省沈阳铁路实验中学2018-2019学年高二下学期期中考试数学(理)试题
名校
4 . 函数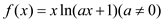 .
.
(Ⅰ)讨论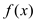 的单调性;
的单调性;
(Ⅱ)若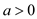 且满足:对
且满足:对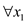 ,
, ,都有
,都有 ,试比较
,试比较 与
与 的大小,并证明.
的大小,并证明.
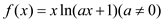 .
.(Ⅰ)讨论
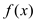 的单调性;
的单调性;(Ⅱ)若
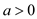 且满足:对
且满足:对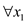 ,
, ,都有
,都有 ,试比较
,试比较 与
与 的大小,并证明.
的大小,并证明.
您最近一年使用:0次
5 . 已知函数 为
为 的导函数.
的导函数.
(Ⅰ)令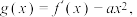 求
求 的单调区间;
的单调区间;
(Ⅱ)证明: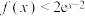
 为
为 的导函数.
的导函数.(Ⅰ)令
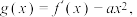 求
求 的单调区间;
的单调区间;(Ⅱ)证明:
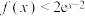
您最近一年使用:0次
6 . 已知函数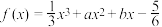
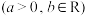 ,
, 在
在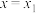 和
和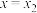 处取得极值,且
处取得极值,且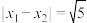 ,曲线
,曲线 在
在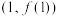 处的切线与直线
处的切线与直线 垂直.
垂直.
(1)求 的解析式;
的解析式;
(2)证明关于 的方程
的方程 至多只有两个实数根(其中
至多只有两个实数根(其中 是
是 的导函数,
的导函数, 是自然对数的底数).
是自然对数的底数).
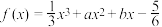
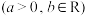 ,
, 在
在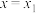 和
和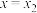 处取得极值,且
处取得极值,且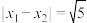 ,曲线
,曲线 在
在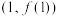 处的切线与直线
处的切线与直线 垂直.
垂直.(1)求
 的解析式;
的解析式;(2)证明关于
 的方程
的方程 至多只有两个实数根(其中
至多只有两个实数根(其中 是
是 的导函数,
的导函数, 是自然对数的底数).
是自然对数的底数).
您最近一年使用:0次
2017-05-16更新
|
943次组卷
|
2卷引用:福建省三明市2017届普通高中高三毕业班5月质量检查数学(文)试题
名校
7 . 已知函数 在
在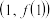 处的切线方程为
处的切线方程为 .
.
(1)求 的单调区间与最小值;
的单调区间与最小值;
(2)求证: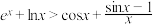 .
.
 在
在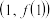 处的切线方程为
处的切线方程为 .
.(1)求
 的单调区间与最小值;
的单调区间与最小值;(2)求证:
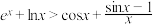 .
.
您最近一年使用:0次
2017-05-09更新
|
1862次组卷
|
5卷引用:福建省泉州市2017届高三高考考前适应性模拟(一)数学(理)试题
名校
8 . 已知函数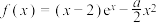 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(1)函数 的图象能否与
的图象能否与 轴相切?若能与
轴相切?若能与 轴相切,求实数
轴相切,求实数 的值;否则,请说明理由;
的值;否则,请说明理由;
(2)若函数 在
在 上单调递增,求实数
上单调递增,求实数 能取到的最大整数值.
能取到的最大整数值.
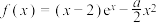 ,其中
,其中 为自然对数的底数.
为自然对数的底数.(1)函数
 的图象能否与
的图象能否与 轴相切?若能与
轴相切?若能与 轴相切,求实数
轴相切,求实数 的值;否则,请说明理由;
的值;否则,请说明理由;(2)若函数
 在
在 上单调递增,求实数
上单调递增,求实数 能取到的最大整数值.
能取到的最大整数值.
您最近一年使用:0次
2017-04-29更新
|
207次组卷
|
2卷引用:福建省莆田第六中学2017届高三下学期第二次模拟数学(理)试题
9 . 已知点 ,直线
,直线 ,直线
,直线 垂直
垂直 于点
于点 ,线段
,线段 的垂直平分线交
的垂直平分线交 于点
于点 .
.
(1)求点 的轨迹
的轨迹 的方程;
的方程;
(2)已知点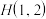 ,过
,过 且与
且与 轴不垂直的直线交
轴不垂直的直线交 于
于 两点,直线
两点,直线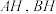 分别交
分别交 于点
于点 ,求证:以
,求证:以 为直径的圆必过定点.
为直径的圆必过定点.
 ,直线
,直线 ,直线
,直线 垂直
垂直 于点
于点 ,线段
,线段 的垂直平分线交
的垂直平分线交 于点
于点 .
.(1)求点
 的轨迹
的轨迹 的方程;
的方程;(2)已知点
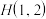 ,过
,过 且与
且与 轴不垂直的直线交
轴不垂直的直线交 于
于 两点,直线
两点,直线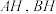 分别交
分别交 于点
于点 ,求证:以
,求证:以 为直径的圆必过定点.
为直径的圆必过定点.
您最近一年使用:0次
名校
10 . 已知函数f(x)=(ax-1)ex,(a∈R).
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)当m>n>0时,证明:men+n<nem+m.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)当m>n>0时,证明:men+n<nem+m.
您最近一年使用:0次
2017-04-11更新
|
1045次组卷
|
8卷引用:2017届福建省高三4月单科质量检测数学文试卷
2017届福建省高三4月单科质量检测数学文试卷河北省定州中学2017届高三下学期第二次月考(4月)数学试题湖南省岳阳市一中2018届高三上学期第一次月考数学(文)试题陕西省吴起高级中学2018届高三上学期期中考试数学(文)试题陕西省宝鸡中学2019届高三年级第二次模拟数学(文科)试题【市级联考】陕西省宝鸡市2019届高三高考模拟检测(二)数学(文科)试题安徽省阜阳市太和中学2021届高三下学期高考押题文科数学试题(已下线)专题3-6 导数压轴大题归类(1)-2022年高考数学毕业班二轮热点题型归纳与变式演练(全国通用)



