名校
解题方法
1 . 已知函数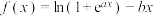 是偶函数,
是偶函数, 是自然对数的底数,
是自然对数的底数,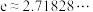
(1)求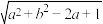 的最小值
的最小值
(2)当 时,
时,
(i)令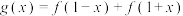 ,
, ,求
,求 的值域
的值域
(ii)记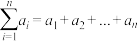 ,已知
,已知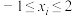 ,
,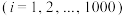 ,且
,且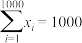 ,当
,当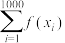 取最大值时,求
取最大值时,求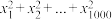 的值.
的值.
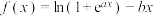 是偶函数,
是偶函数, 是自然对数的底数,
是自然对数的底数,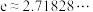
(1)求
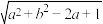 的最小值
的最小值
(2)当
 时,
时,(i)令
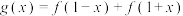 ,
, ,求
,求 的值域
的值域
(ii)记
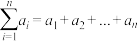 ,已知
,已知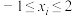 ,
,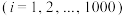 ,且
,且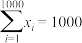 ,当
,当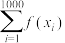 取最大值时,求
取最大值时,求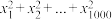 的值.
的值.
您最近一年使用:0次
2024-10-30更新
|
307次组卷
|
2卷引用:广东省雷州市龙门中学、客路中学两校2024-2025学年高三上学期十月第一次模拟考试数学试题
2 . 已知函数 .
.
(1)解关于 的不等式
的不等式 ;
;
(2)若关于 的方程
的方程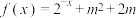 在
在 上有实数解,求实数
上有实数解,求实数 的取值范围;
的取值范围;
(3)若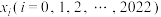 将区间
将区间 划分成2022个小区间,且满足
划分成2022个小区间,且满足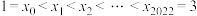 ,试判断和式
,试判断和式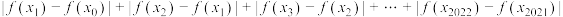 是否为定值,若是,请求出这个值,若不是请说明理由.
是否为定值,若是,请求出这个值,若不是请说明理由.
 .
.(1)解关于
 的不等式
的不等式 ;
;(2)若关于
 的方程
的方程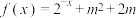 在
在 上有实数解,求实数
上有实数解,求实数 的取值范围;
的取值范围;(3)若
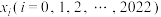 将区间
将区间 划分成2022个小区间,且满足
划分成2022个小区间,且满足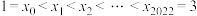 ,试判断和式
,试判断和式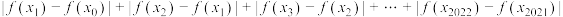 是否为定值,若是,请求出这个值,若不是请说明理由.
是否为定值,若是,请求出这个值,若不是请说明理由.
您最近一年使用:0次
名校
解题方法
3 . 已知函数 ,若对于其定义域
,若对于其定义域 中任意给定的实数
中任意给定的实数 ,都有
,都有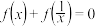 ,就称函数
,就称函数 满足性质
满足性质 .
.
(1)已知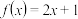 ,判断
,判断 是否满足性质
是否满足性质 ,并说明理由;
,并说明理由;
(2)若 满足性质
满足性质 ,且定义域为
,且定义域为 .
.
 已知
已知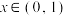 时,
时,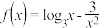 ,求函数
,求函数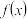 的解析式并指出方程
的解析式并指出方程 是否有正整数解?请说明理由;
是否有正整数解?请说明理由;
 若
若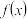 在
在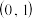 上单调递增,判定并证明
上单调递增,判定并证明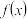 在
在 上的单调性.
上的单调性.
 ,若对于其定义域
,若对于其定义域 中任意给定的实数
中任意给定的实数 ,都有
,都有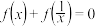 ,就称函数
,就称函数 满足性质
满足性质 .
.(1)已知
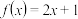 ,判断
,判断 是否满足性质
是否满足性质 ,并说明理由;
,并说明理由;(2)若
 满足性质
满足性质 ,且定义域为
,且定义域为 .
. 已知
已知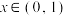 时,
时,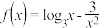 ,求函数
,求函数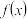 的解析式并指出方程
的解析式并指出方程 是否有正整数解?请说明理由;
是否有正整数解?请说明理由; 若
若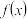 在
在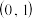 上单调递增,判定并证明
上单调递增,判定并证明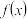 在
在 上的单调性.
上的单调性.
您最近一年使用:0次
2024-03-04更新
|
196次组卷
|
2卷引用:重庆市万州第一中学2023-2024学年高一下学期入学考试数学试卷
4 . 已知幂函数 的图象关于原点对称.
的图象关于原点对称.
(1)求实数m的值;
(2)设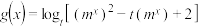 ,(
,( 且
且 ),若不等式
),若不等式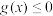 对任意
对任意 恒成立,求t的取值范围.
恒成立,求t的取值范围.
 的图象关于原点对称.
的图象关于原点对称.(1)求实数m的值;
(2)设
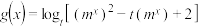 ,(
,( 且
且 ),若不等式
),若不等式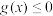 对任意
对任意 恒成立,求t的取值范围.
恒成立,求t的取值范围.
您最近一年使用:0次
名校
解题方法
5 . 已知x满足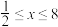 .
.
(1)求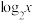 的取值范围;
的取值范围;
(2)求函数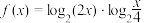 的最小值.
的最小值.
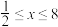 .
.(1)求
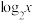 的取值范围;
的取值范围;(2)求函数
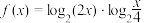 的最小值.
的最小值.
您最近一年使用:0次
2023-12-26更新
|
432次组卷
|
5卷引用:河南省洛阳市强基联盟2023-2024学年高一上学期12月联考数学试题
名校
解题方法
6 . 已知函数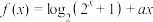 是偶函数.
是偶函数.
(1)求 的值;
的值;
(2)设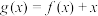 ,
,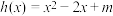 ,若对任意的
,若对任意的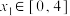 ,存在
,存在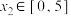 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
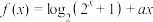 是偶函数.
是偶函数.(1)求
 的值;
的值;(2)设
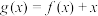 ,
,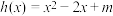 ,若对任意的
,若对任意的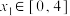 ,存在
,存在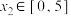 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-10-31更新
|
4269次组卷
|
27卷引用:全国名校大联考2023-2024学年高三上学期第一联考(月考)数学试题
全国名校大联考2023-2024学年高三上学期第一联考(月考)数学试题陕西省榆林市府谷县第一中学2023-2024学年高三上学期第一次联考理科数学试题河北省保定市唐县第一中学2024届高三上学期9月月考数学试题江西省2024届高三上学期一轮复习联考数学试题(已下线)专题4.6 指、对数函数的综合应用大题专项训练-举一反三系列福建省宁德第一中学2024届高三上学期学科素养训练(二模)数学试题贵州省2024届高三上学期第一次联考(月考)数学试题吉林省通榆县第一中学校2024届高三上学期第二次质量检测数学试题河北省衡水市武强中学2024届高三上学期期中数学试题新疆乌鲁木齐市第七十中学2024届高三上学期第一次联考(月考)数学试题新疆维吾尔自治区喀什第二中学2023-2024学年高三上学期期中测试数学试题湖北省宜昌市协作体2023-2024学年高三上学期期中考试数学试题四川省2024届高三上学期第一次联考(月考)理科数学试题四川省2024届高三上学期第一次联考(月考)文科数学试题甘肃省天水市麦积区天水三中、天水九中、新梦想高考复读学校2023-2024学年高三上学期11月大联考数学试卷贵州省黔西南州金成实验学校2023-2024学年高一上学期第三次质量检测数学试题(已下线)高一上学期数学期末考测试卷(提升)-《一隅三反》(已下线)第6章 幂函数、指数函数和对数函数章末题型归纳总结 (1)-【帮课堂】(苏教版2019必修第一册)云南省昆明市第八中学2023-2024学年高一上学期12月月考数学试题(已下线)专题06 对数函数2-期末复习重难培优与单元检测(人教A版2019)山东省青岛市四校联考2023-2024学年高一下学期期中考试数学试题(已下线)第05讲 对数与对数函数(八大题型)(练习)-2(已下线)2.5 对数运算及对数函数-2新疆昌吉州行知学校2024届高三复读班上学期第一次月考数学试卷专题09对数运算与对数函数江西省乐平市私立洪马中学2024-2025学年高一上学期重点班10月月考数学试卷贵州省黔西南州顶兴高级中学2024-2025学年高三上学期第二次月考数学试卷
7 . 已知函数 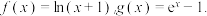
(1)判断函数 的零点个数;
的零点个数;
(2)比较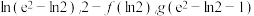 的大小.
的大小.
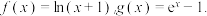
(1)判断函数
 的零点个数;
的零点个数;(2)比较
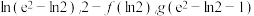 的大小.
的大小.
您最近一年使用:0次
8 . 已知函数 .
.
(1)当 时,判断函数
时,判断函数 的单调性,并写出单调区间(无需证明);
的单调性,并写出单调区间(无需证明);
(2)若存在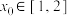 ,使
,使 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 .
.(1)当
 时,判断函数
时,判断函数 的单调性,并写出单调区间(无需证明);
的单调性,并写出单调区间(无需证明);(2)若存在
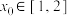 ,使
,使 成立,求实数
成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
解题方法
9 . 已知函数 .
.
(1)若函数 ,判断
,判断 的奇偶性并证明;
的奇偶性并证明;
(2)对 ,不等式
,不等式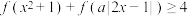 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 .
.(1)若函数
 ,判断
,判断 的奇偶性并证明;
的奇偶性并证明;(2)对
 ,不等式
,不等式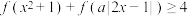 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
10 . 已知函数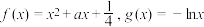 .
.
(1)若函数 在
在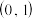 上有两个不同的零点,求实数
上有两个不同的零点,求实数 的取值范围;
的取值范围;
(2)用 表示
表示 中的最小值,设函数
中的最小值,设函数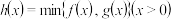 ,讨论
,讨论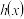 零点的个数.
零点的个数.
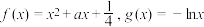 .
.(1)若函数
 在
在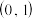 上有两个不同的零点,求实数
上有两个不同的零点,求实数 的取值范围;
的取值范围;(2)用
 表示
表示 中的最小值,设函数
中的最小值,设函数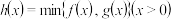 ,讨论
,讨论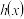 零点的个数.
零点的个数.
您最近一年使用:0次
2022-05-19更新
|
1272次组卷
|
6卷引用:江苏省南京市六校2021-2022学年高一下学期期中联考数学试题
江苏省南京市六校2021-2022学年高一下学期期中联考数学试题广东省广州市六中2022-2023学年高二上学期期中(线上)数学试题广东省广州市第六中学2022-2023学年高二上学期期中数学试题(已下线)4.5.1 函数零点与方程的解(分层作业)-【上好课】(已下线)4.5.1 函数零点与方程的解(导学案)-【上好课】陕西省西安市西安交大附中2023-2024学年高一上学期第二次月考数学试题



