解题方法
1 . 下列结论中正确的是( )
A. 的最小值为 的最小值为 |
B.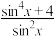 的最小值为 的最小值为 |
C. 的最小值为 的最小值为 |
D.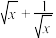 的最小值为 的最小值为 |
您最近一年使用:0次
名校
2 . 已知函数 .
.
(1)写出 的最小正周期;
的最小正周期;
(2)求 的最小值,并求取得最小值时自变量
的最小值,并求取得最小值时自变量 的集合.
的集合.
 .
.(1)写出
 的最小正周期;
的最小正周期;(2)求
 的最小值,并求取得最小值时自变量
的最小值,并求取得最小值时自变量 的集合.
的集合.
您最近一年使用:0次
2023-01-30更新
|
1626次组卷
|
3卷引用:内蒙古巴彦淖尔市临河区第三中学2021-2022学年高一上学期期末考试数学试题
3 . 设函数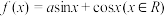
(1)当 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)当 时,求函数
时,求函数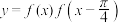 在
在 上的值域.
上的值域.
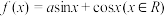
(1)当
 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;(2)当
 时,求函数
时,求函数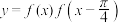 在
在 上的值域.
上的值域.
您最近一年使用:0次
名校
4 . 已知向量 ,
, ,函数
,函数 .
.
(1)求函数 的最小正周期及单调增区间.
的最小正周期及单调增区间.
(2)将函数 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 的图象,求
的图象,求 在
在 上的值域.
上的值域.
 ,
, ,函数
,函数 .
.(1)求函数
 的最小正周期及单调增区间.
的最小正周期及单调增区间.(2)将函数
 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 的图象,求
的图象,求 在
在 上的值域.
上的值域.
您最近一年使用:0次
2021-11-05更新
|
462次组卷
|
3卷引用:内蒙古海拉尔第二中学2021-2022学年高三上学期第二次阶段考数学(文)试题
名校
解题方法
5 . 函数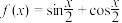 的最小正周期和最大值分别是( )
的最小正周期和最大值分别是( )
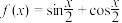 的最小正周期和最大值分别是( )
的最小正周期和最大值分别是( )A.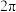 和 和 | B.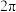 和2 和2 | C. 和 和 | D. 和2 和2 |
您最近一年使用:0次
2021-10-21更新
|
1831次组卷
|
6卷引用:内蒙古自治区赤峰市2020-2021学年高一下学期期末联考文科数学试题(A)
内蒙古自治区赤峰市2020-2021学年高一下学期期末联考文科数学试题(A)甘肃省嘉峪关市第一中学2020-2021学年高一下学期期末数学试题江苏省扬州中学2021-2022学年高三上学期10月阶段检测数学试题宁夏青铜峡市高级中学2022届高三11月测试数学(文)试题(已下线)考点13 三角函数与三角恒等变换-2022年高考数学一轮复习小题多维练(新高考版)山东省青岛市海尔学校2023-2024学年高一下学期期中考试数学试卷
6 . 已知 .
.
(1)求 的单调区间以及对称中心;
的单调区间以及对称中心;
(2)当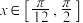 时,求
时,求 的值域.
的值域.
 .
.(1)求
 的单调区间以及对称中心;
的单调区间以及对称中心;(2)当
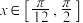 时,求
时,求 的值域.
的值域.
您最近一年使用:0次
名校
7 . 已知函数 .
.
(1)求函数 在区间
在区间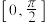 上的最小值;
上的最小值;
(2)若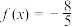 ,
,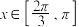 ,求
,求 的值.
的值.
 .
.(1)求函数
 在区间
在区间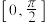 上的最小值;
上的最小值;(2)若
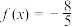 ,
,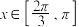 ,求
,求 的值.
的值.
您最近一年使用:0次
2021-10-18更新
|
518次组卷
|
2卷引用:内蒙古鄂尔多斯市第一中学2021-2022学年高二上学期第一次月考数学(文)试题
名校
解题方法
8 . 在锐角三角形 中,内角
中,内角 的对边分别为
的对边分别为 .若
.若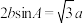 ,则
,则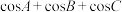 的取值范围是
的取值范围是_______
 中,内角
中,内角 的对边分别为
的对边分别为 .若
.若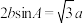 ,则
,则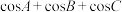 的取值范围是
的取值范围是
您最近一年使用:0次
2021-09-14更新
|
1467次组卷
|
6卷引用:内蒙古自治区包头市2020-2021学年高一下学期期末数学试题
内蒙古自治区包头市2020-2021学年高一下学期期末数学试题上海市复兴高级中学2020-2021学年高一下学期期中数学试题甘肃省张掖市第二中学2021-2022学年高二上学期10月月考数学 理科(B)试题(已下线)第六章 平面向量及其应用 章末测试(提升)-2021-2022学年高一数学一隅三反系列(人教A版2019必修第二册)四川省成都市武侯区成都市武侯高级中学2023-2024学年高二上学期10月月考数学试题河北省邯郸市育华中学2022-2023学年高一下学期期中考试数学试卷
9 . 如图,已知直线 ∥
∥ ,
, 为
为 之间的定点,并且
之间的定点,并且 到
到 的距离分别为
的距离分别为 ,点
,点 分别是直线
分别是直线 上的动点,使得
上的动点,使得 .过点
.过点 作直线
作直线 ,交
,交 于点
于点 ,交
,交 于点
于点 ,设
,设 .
.
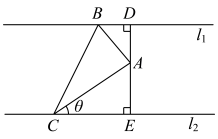
(1)求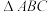 的面积
的面积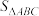 关于
关于 的解析式
的解析式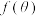 ;
;
(2)求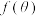 的最小值及取得最小值时
的最小值及取得最小值时 的值.
的值.
 ∥
∥ ,
, 为
为 之间的定点,并且
之间的定点,并且 到
到 的距离分别为
的距离分别为 ,点
,点 分别是直线
分别是直线 上的动点,使得
上的动点,使得 .过点
.过点 作直线
作直线 ,交
,交 于点
于点 ,交
,交 于点
于点 ,设
,设 .
.
(1)求
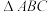 的面积
的面积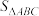 关于
关于 的解析式
的解析式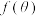 ;
;(2)求
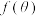 的最小值及取得最小值时
的最小值及取得最小值时 的值.
的值.
您最近一年使用:0次
2021-09-14更新
|
158次组卷
|
2卷引用:内蒙古自治区包头市2020-2021学年高一下学期期末数学试题
名校
解题方法
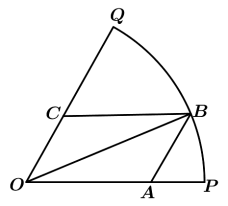
10 . 如图,现要在一块半径为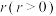 ,圆心角为
,圆心角为 的扇形纸板
的扇形纸板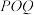 上剪出一个平行四边形
上剪出一个平行四边形 ,使点
,使点 在弧
在弧 上,点
上,点 在半径
在半径 上,点
上,点 在半径
在半径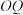 上.设
上.设 ,平行四边形
,平行四边形 的面积为
的面积为 .
.
(1)求 关于
关于 的函数关系式;
的函数关系式;
(2)求 的最大值及相应的
的最大值及相应的 值.
值.
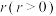 ,圆心角为
,圆心角为 的扇形纸板
的扇形纸板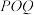 上剪出一个平行四边形
上剪出一个平行四边形 ,使点
,使点 在弧
在弧 上,点
上,点 在半径
在半径 上,点
上,点 在半径
在半径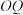 上.设
上.设 ,平行四边形
,平行四边形 的面积为
的面积为 .
.
(1)求
 关于
关于 的函数关系式;
的函数关系式;(2)求
 的最大值及相应的
的最大值及相应的 值.
值.
您最近一年使用:0次



