名校
解题方法
1 . 记 的内角
的内角 的对边分别为
的对边分别为 ,已知
,已知 .
.
(1)求 ;
;
(2)设 的中点为
的中点为 ,若
,若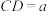 ,且
,且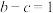 ,求
,求 的的面积.
的的面积.
 的内角
的内角 的对边分别为
的对边分别为 ,已知
,已知 .
.(1)求
 ;
;(2)设
 的中点为
的中点为 ,若
,若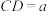 ,且
,且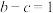 ,求
,求 的的面积.
的的面积.
您最近一年使用:0次
2023-02-17更新
|
7042次组卷
|
11卷引用:浙江省湖州市2022-2023学年高二下学期期末数学试题
(已下线)浙江省湖州市2022-2023学年高二下学期期末数学试题广东省深圳市2023届高三第一次调研数学试题(已下线)模块八 三角函数与解三角形-2福建省福州第三中学2023届高三第十二次质量检测数学试题广东省番禺中学2022-2023学年高二下学期3月月考数学试题广东省清远市阳山县南阳中学2022-2023学年高二下学期第一次月考数学试题专题10解三角形重庆市2023届高三临门一卷(二) 数学试题广东省广州市真光中学2022-2023学年高一下学期5月阶段质量检测数学试题陕西省西安市高新第一中学2023-2024学年高二上学期联考数学试题(已下线)6.4.3.2 正弦定理——课后作业(巩固版)
解题方法
2 . 记 的内角A,B,C的对边分别为a,b,c,已知
的内角A,B,C的对边分别为a,b,c,已知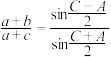 .
.
(1)若 ,求B;
,求B;
(2)求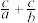 的取值范围.
的取值范围.
 的内角A,B,C的对边分别为a,b,c,已知
的内角A,B,C的对边分别为a,b,c,已知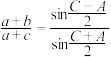 .
.(1)若
 ,求B;
,求B;(2)求
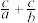 的取值范围.
的取值范围.
您最近一年使用:0次
2023-01-27更新
|
4699次组卷
|
3卷引用:浙江省数海漫游2023届高三下学期一模数学试题
名校
3 . 在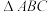 中,内角
中,内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, .若
.若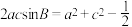 ,且
,且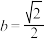 .
.
(1)求角 的大小;
的大小;
(2)若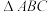 的面积为
的面积为 ,求
,求 的最大值.
的最大值.
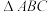 中,内角
中,内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, .若
.若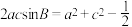 ,且
,且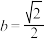 .
.(1)求角
 的大小;
的大小;(2)若
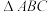 的面积为
的面积为 ,求
,求 的最大值.
的最大值.
您最近一年使用:0次
2019-10-31更新
|
29290次组卷
|
8卷引用:【新东方】双师202高一下
名校
解题方法
4 .  的内角A,B,C的对边分别为a,b,c,已知A为锐角,
的内角A,B,C的对边分别为a,b,c,已知A为锐角,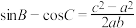 .
.
(1)求A;
(2)若 ,且
,且 边上的高为
边上的高为 ,求
,求 的面积.
的面积.
 的内角A,B,C的对边分别为a,b,c,已知A为锐角,
的内角A,B,C的对边分别为a,b,c,已知A为锐角,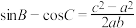 .
.(1)求A;
(2)若
 ,且
,且 边上的高为
边上的高为 ,求
,求 的面积.
的面积.
您最近一年使用:0次
2021-03-18更新
|
10464次组卷
|
18卷引用:专题6.6 第六章 《平面向量》综合测试卷(B卷提升篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教A版,浙江专用)
(已下线)专题6.6 第六章 《平面向量》综合测试卷(B卷提升篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教A版,浙江专用)(已下线)押第18题三角函数-备战2021年高考数学临考题号押题(浙江专用)广东省深圳市2021届高三一模数学试题湖南省邵阳市邵东市第一中学2020-2021学年高二下学期期中数学试题江西省宜春市铜鼓中学2020-2021学年高一(实验班)下学期第一次月考数学(文)试题(已下线)专题2.1 解三角形-常规型-2021年高考数学解答题挑战满分专项训练(新高考地区专用)广东省广州市广州大学附属中学2021-2022学年高二上学期第一次月考数学试题广东省汕头市金山中学2022届高三上学期期中数学试题(已下线)第六章 平面向量及其应用单元自测卷(一)(已下线)专题12 中线、高线、角平分线问题-【重难点突破】2021-2022学年高一数学常考题专练(人教A版2019必修第二册) 广东省深圳市高级中学2022-2023学年高二上学期期中数学试题河南省郑州市郑州外国语学校2021-2022学年高一下学期期中数学试题湖南省株洲市茶陵县2021-2022学年高二下学期期末数学试题广东省佛山市S7高质量发展联盟2022-2023学年高一下学期第一次联考(4月)数学试题广东省广州市天河区2024届高三上学期普通高中毕业班综合测试(一)数学试题广东省广州市第六十五中学2024届高三上学期11月月考数学试题河南省济源市英才学校2023-2024学年高二上学期11月月考数学试题福建省漳州市东山第二中学2023届高三上学期期中数学试题
名校
解题方法
5 . 已知 满足
满足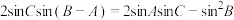 .
.
(1)试问:角 是否可能为直角?请说明理由;
是否可能为直角?请说明理由;
(2)若 为锐角三角形,求
为锐角三角形,求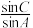 的取值范围.
的取值范围.
 满足
满足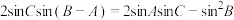 .
.(1)试问:角
 是否可能为直角?请说明理由;
是否可能为直角?请说明理由;(2)若
 为锐角三角形,求
为锐角三角形,求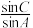 的取值范围.
的取值范围.
您最近一年使用:0次
2023-03-26更新
|
2824次组卷
|
8卷引用:浙江省温州市普通高中2023届高三下学期3月第二次适应性考试数学试题
浙江省温州市普通高中2023届高三下学期3月第二次适应性考试数学试题(已下线)专题03 三角函数及解三角形安徽省合肥市第八中学2022-2023学年高一下学期期中检测数学试题(已下线)专题04 三角函数-2(已下线)模块六 专题6易错题目重组卷(浙江卷)安徽省安庆市桐城中学2023届高三下学期第二次模拟数学试卷广东省中山市2022-2023学年高一下学期期末数学试题(已下线)专题08 解三角形-2
20-21高一下·浙江·期末
名校
6 . 在锐角 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,若
,若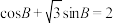 ,
,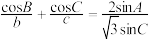 .
.
(1)求角 的大小和边长
的大小和边长 的值;
的值;
(2)求 面积的最大值.
面积的最大值.
 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,若
,若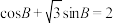 ,
,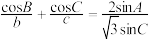 .
.(1)求角
 的大小和边长
的大小和边长 的值;
的值;(2)求
 面积的最大值.
面积的最大值.
您最近一年使用:0次
2021-06-12更新
|
9220次组卷
|
12卷引用:【新东方】在线数学173高一下
(已下线)【新东方】在线数学173高一下浙江省舟山中学2021-2022学年高三上学期12月月考数学试题(已下线)考点16 三角函数的图象与性质-备战2022年高考数学(理)一轮复习考点帮(已下线)考点15 三角函数的图象与性质-备战2022年高考数学(文)一轮复习考点帮(已下线)2020年高考浙江数学高考真题变式题17-22题河南省洛阳第一高级中学2021-2022学年高三上学期10月月考数学理科试题(已下线)第六章 平面向量及其应用 章末测试(提升)-2021-2022学年高一数学一隅三反系列(人教A版2019必修第二册)(已下线)第21节 解三角形吉林省长春市实验中学2022-2023学年高三上学期二模考试数学试题陕西省西安高新唐南中学2022-2023学年高一下学期期中数学试题黑龙江省牡丹江市第一高级中学2022-2023学年高一下学期期中数学试题专题05正弦定理、余弦定理解三角形(解答题)
名校
解题方法
7 . 在 中,内角
中,内角 的对边分别为
的对边分别为 ,向量
,向量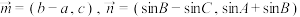 ,且
,且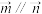 .
.
(1)求 ;
;
(2)若 的外接圆半径为2,且
的外接圆半径为2,且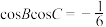 ,求
,求 的面积.
的面积.
 中,内角
中,内角 的对边分别为
的对边分别为 ,向量
,向量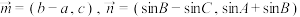 ,且
,且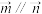 .
.(1)求
 ;
;(2)若
 的外接圆半径为2,且
的外接圆半径为2,且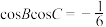 ,求
,求 的面积.
的面积.
您最近一年使用:0次
2024-01-12更新
|
2686次组卷
|
4卷引用:浙江省宁波市镇海中学2024届高三上学期期末数学试题
名校
解题方法
8 . 在锐角 中,内角
中,内角 所对的边分别为
所对的边分别为 ,
, ,
, ,满足
,满足 ,且
,且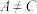 .
.
(1)求证: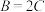 ;
;
(2)已知 是
是 的平分线,若
的平分线,若 ,求线段
,求线段 长度的取值范围.
长度的取值范围.
 中,内角
中,内角 所对的边分别为
所对的边分别为 ,
, ,
, ,满足
,满足 ,且
,且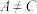 .
.(1)求证:
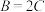 ;
;(2)已知
 是
是 的平分线,若
的平分线,若 ,求线段
,求线段 长度的取值范围.
长度的取值范围.
您最近一年使用:0次
2023-08-12更新
|
2605次组卷
|
14卷引用:浙江省湖州、衢州、丽水三地市2023届高三下学期4月教学质量检测(二模)数学试题
浙江省湖州、衢州、丽水三地市2023届高三下学期4月教学质量检测(二模)数学试题(已下线)专题03 三角函数及解三角形浙江省嘉兴市秀水高级中学2022-2023学年高二下学期5月月考数学试题(已下线)数学(云南,安徽,黑龙江,山西,吉林五省新高考专用)(已下线)押新高考第17题 解三角形黑龙江省哈尔滨德强高中2022-2023学年高一下学期期中考试数学试题(已下线)模块二 专题3 解三角形与不等式河南省实验中学2023-2024学年高三上学期第一次月考数学试题(已下线)河南省实验中学2023-2024学年高三上学期第一次月考数学试题变式题15-18理科数学-【名校面对面】河南省三甲名校2023届高三校内模拟试题(五)(已下线)专题02 解三角形大题江苏省南通市2024届高三高考考前押题卷(最后一卷)数学试题2024届山东省五莲县第一中学高三模拟预测数学试题(已下线)解三角形02-一轮复习考点专练
名校
解题方法
9 . 在锐角 中,设边
中,设边 所对的角分别为
所对的角分别为 ,且
,且 .
.
(1)证明:
(2)若 ,求
,求 的取值范围.
的取值范围.
 中,设边
中,设边 所对的角分别为
所对的角分别为 ,且
,且 .
.(1)证明:

(2)若
 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-10-10更新
|
3053次组卷
|
6卷引用:浙江省湖州市第二中学2024届高三上学期期中数学试题
浙江省湖州市第二中学2024届高三上学期期中数学试题浙江省湖州市第一中学2024届高三下学期新高考数学模拟试题黑龙江省哈尔滨市第六中学校2024年高三上学期10月月考数学试题(已下线)第11讲 6.4.3 第2课时 正弦定理 (1)-【帮课堂】(人教A版2019必修第二册)第17讲 第六章 平面向量及其应用 章节验收测评卷-【帮课堂】2023-2024学年高一数学同步学与练(人教A版2019必修第二册)(已下线)6.4.3.2 正弦定理——课后作业(基础版)
名校
解题方法
10 . 已知函数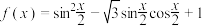 .
.
(1)求函数 的单调递减区间;
的单调递减区间;
(2)在 中,内角A,B,C的对边分别为a,b,c,且满足
中,内角A,B,C的对边分别为a,b,c,且满足 ,求
,求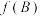 的取值范围.
的取值范围.
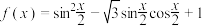 .
.(1)求函数
 的单调递减区间;
的单调递减区间;(2)在
 中,内角A,B,C的对边分别为a,b,c,且满足
中,内角A,B,C的对边分别为a,b,c,且满足 ,求
,求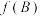 的取值范围.
的取值范围.
您最近一年使用:0次
2022-02-23更新
|
4882次组卷
|
15卷引用:浙江省名校协作体2021-2022学年高二下学期开学考试数学试题
浙江省名校协作体2021-2022学年高二下学期开学考试数学试题浙江省台州市书生中学2021-2022学年高二下学期起始考数学试题(已下线)专题04 平面向量的应用-2021-2022学年高一《新题速递·数学》(人教A版2019)余弦定理、正弦定理应用举例(已下线)第六章 平面向量及其应用 讲核心 02(已下线)专题12 盘点解三角形中最值问题的四种方法-1(已下线)第09讲 解三角形中解答题4种基础题型上海市格致中学2023届高三下学期3月阶段性测试数学试题(已下线)上海市华东师范大学第二附属中学2023届高三最后一模数学试题(已下线)专题6.8 解三角形的综合应用大题专项训练-举一反三系列上海市浦东新区建平中学2024届高三下学期2月考试数学试卷(已下线)专题4.3 正弦定理和余弦定理【八大题型】(已下线)重难点08 正、余弦定理解三角形的重要模型和综合应用【八大题型】(已下线)黄金卷04(已下线)第04讲 解三角形(九大题型)(讲义)-1



