名校
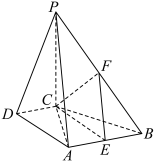
1 . 如图,在四棱锥 中,
中, 平面
平面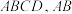

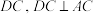 .
.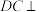 平面
平面 ;
;
(2)若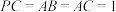 ,求
,求 与平面
与平面 成角的正弦值;
成角的正弦值;
(3)设点 为
为 的中点,过点
的中点,过点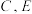 的平面与棱
的平面与棱 交于点
交于点 ,且
,且
 平面
平面 ,求
,求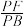 的值.
的值.
 中,
中, 平面
平面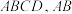

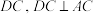 .
.
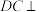 平面
平面 ;
;(2)若
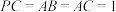 ,求
,求 与平面
与平面 成角的正弦值;
成角的正弦值;(3)设点
 为
为 的中点,过点
的中点,过点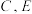 的平面与棱
的平面与棱 交于点
交于点 ,且
,且
 平面
平面 ,求
,求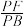 的值.
的值.
您最近一年使用:0次
2024-10-12更新
|
679次组卷
|
3卷引用:辽宁省七校2024-2025学年高二上学期期初考试数学试卷
名校
2 . 已知正方体 的棱长为
的棱长为 ,
, 是线段
是线段 上的动点,则( )
上的动点,则( )
 的棱长为
的棱长为 ,
, 是线段
是线段 上的动点,则( )
上的动点,则( )A. |
B.二面角 的正切值为 的正切值为 |
C.直线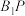 与平面 与平面 所成最小角的正弦值为 所成最小角的正弦值为 |
D.若 是对角线 是对角线 上一点,则 上一点,则 的最小值为 的最小值为 |
您最近一年使用:0次
2024-09-04更新
|
438次组卷
|
2卷引用:辽宁省抚顺市第一中学2024-2025学年高二上学期期初考试数学试题
名校
解题方法
3 . 若某圆锥的侧面积为底面积的2倍,则该圆锥的母线与底面所成角的正切值为______ .
您最近一年使用:0次
2024-03-06更新
|
421次组卷
|
3卷引用:辽宁省名校联盟2023-2024学年高二下学期3月联合考试数学试卷
4 . 已知 是圆锥
是圆锥 的底面圆
的底面圆 的直径,
的直径, 分别是底面圆
分别是底面圆 的圆周上的点,且
的圆周上的点,且 ,
,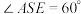 ,
,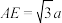 ,
, 为
为 的中点,则( )
的中点,则( )
 是圆锥
是圆锥 的底面圆
的底面圆 的直径,
的直径, 分别是底面圆
分别是底面圆 的圆周上的点,且
的圆周上的点,且 ,
,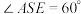 ,
,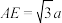 ,
, 为
为 的中点,则( )
的中点,则( )A.平面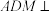 平面 平面 | B.三棱锥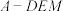 的体积为 的体积为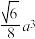 |
C.异面直线 与 与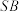 所成角为 所成角为 | D.直线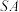 与平面 与平面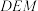 所成角为 所成角为 |
您最近一年使用:0次
名校
5 . 在棱长为1的正方体 中,
中, 为侧面
为侧面 内的一个动点(含边界),则下列说法正确的是( )
内的一个动点(含边界),则下列说法正确的是( )
 中,
中, 为侧面
为侧面 内的一个动点(含边界),则下列说法正确的是( )
内的一个动点(含边界),则下列说法正确的是( )A.随着 点移动,三棱锥 点移动,三棱锥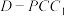 的体积有最小值为 的体积有最小值为 |
B.三棱锥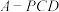 体积的最大值为 体积的最大值为 |
C.直线 与平面 与平面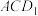 所成角的余弦值为 所成角的余弦值为 |
D.作体对角线 的垂面 的垂面 ,则平面 ,则平面 截此正方体所得截面图形的面积越大,其周长越大 截此正方体所得截面图形的面积越大,其周长越大 |
您最近一年使用:0次
2023-08-12更新
|
912次组卷
|
7卷引用:辽宁省抚顺德才高级中学2023-2024学年高二上学期期初考试数学(北大班)试题
辽宁省抚顺德才高级中学2023-2024学年高二上学期期初考试数学(北大班)试题辽宁省鞍山市台安县高级中学2022-2023学年高一下学期期末数学试题江西省全南中学2023-2024学年高二上学期开学考试数学试题(已下线)湖南省长沙市雅礼中学2024届高三上学期月考(二)数学试题变式题11-14(已下线)专题08立体几何期末14种常考题型归类(2) -期末真题分类汇编(人教B版2019必修第四册)(已下线)专题04 立体几何初步-期期末真题分类汇编(人教A版2019必修第二册)河北省沧州市部分学校2023-2024学年高一下学期5月联考数学试题
名校
6 . 如图,在直三棱柱 中,
中,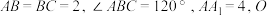 为
为 的中点,
的中点, 为
为 上的动点,
上的动点, 在
在 上,且满足
上,且满足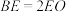 .现延长
.现延长 至
至 点,使得
点,使得 .
.

(1)若二面角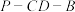 的平面角为
的平面角为 ,求
,求 的长;
的长;
(2)若三棱锥 的体积为
的体积为 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中,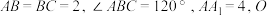 为
为 的中点,
的中点, 为
为 上的动点,
上的动点, 在
在 上,且满足
上,且满足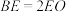 .现延长
.现延长 至
至 点,使得
点,使得 .
.
(1)若二面角
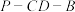 的平面角为
的平面角为 ,求
,求 的长;
的长;(2)若三棱锥
 的体积为
的体积为 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2023-07-27更新
|
1293次组卷
|
6卷引用:辽宁省抚顺德才高级中学2023-2024学年高二上学期期初考试数学(北大班)试题
辽宁省抚顺德才高级中学2023-2024学年高二上学期期初考试数学(北大班)试题辽宁省鞍山市台安县高级中学2022-2023学年高一下学期期末数学试题山西省太原师范学院附属中学(太原市师苑中学校)2023-2024学年高二上学期开学分班测评数学试题江西省南昌市等5地2022-2023学年高一下学期期末联考数学试题(已下线)第八章 立体几何初步(压轴题专练)-单元速记·巧练(人教A版2019必修第二册)(已下线)重组8 高一期末真题重组卷(辽宁卷)A基础卷
7 . 如图,多面体 中,四边形
中,四边形 为平行四边形,
为平行四边形,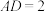 ,
, ,四边形
,四边形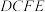 为梯形,
为梯形, ,
, ,
,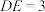 ,
,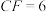 ,
,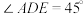 ,平面
,平面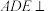 平面
平面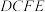 .
.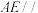 平面
平面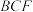 ;
;
(2)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)求点 到平面
到平面 的距离.
的距离.
 中,四边形
中,四边形 为平行四边形,
为平行四边形,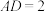 ,
, ,四边形
,四边形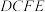 为梯形,
为梯形, ,
, ,
,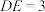 ,
,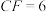 ,
,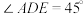 ,平面
,平面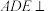 平面
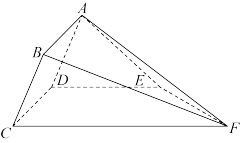
平面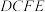 .
.
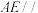 平面
平面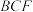 ;
;(2)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(3)求点
 到平面
到平面 的距离.
的距离.
您最近一年使用:0次
2023-07-18更新
|
911次组卷
|
5卷引用:辽宁省抚顺市第一中学2024-2025学年高二上学期期初考试数学试题
辽宁省抚顺市第一中学2024-2025学年高二上学期期初考试数学试题四川省眉山市彭山区第一中学2023-2024学年高二上学期开学考试数学试题四川省巴中市恩阳区恩阳中学2024-2025学年高二上学期开学考试数学试卷四川省成都市成都市石室中学2022-2023学年高一下学期期末数学试题(已下线)【高一模块二】类型4 以立体几何中的位置关系判断为背景的解答题(B卷提升卷)
解题方法
8 . 已知正方体 的棱长为2,则( )
的棱长为2,则( )
 的棱长为2,则( )
的棱长为2,则( )A.直线 与 与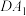 所成的角为 所成的角为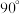 |
B.直线 与 与 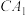 所成的角为 所成的角为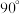 |
C.点 到平面 到平面 的距离为 的距离为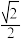 |
D.直线 与平面 与平面 所成的角为 所成的角为 |
您最近一年使用:0次
2022-09-17更新
|
572次组卷
|
2卷引用:辽宁省六校2022-2023学年高三上学期期初考试数学试题
名校
9 . 在棱长为1的正方体 中,点P满足
中,点P满足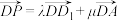 ,
,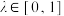 ,
, ,则以下说法正确的是( )
,则以下说法正确的是( )
 中,点P满足
中,点P满足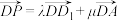 ,
,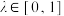 ,
, ,则以下说法正确的是( )
,则以下说法正确的是( )A.当 时,直线 时,直线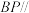 平面 平面 |
B.当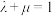 时,线段CP长度的最小值为 时,线段CP长度的最小值为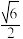 |
C.当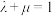 时,直线CP与平面 时,直线CP与平面 所成的角不可能为 所成的角不可能为 |
D.当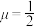 时,存在唯一点P使得直线DP与直线 时,存在唯一点P使得直线DP与直线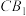 所成的角为 所成的角为 |
您最近一年使用:0次
2021-11-23更新
|
737次组卷
|
20卷引用:辽宁省大连市金普新区省示范性高中联合体2021-2022学年高三第四阶段考试(下学期开学考试)数学试题
辽宁省大连市金普新区省示范性高中联合体2021-2022学年高三第四阶段考试(下学期开学考试)数学试题湖北省恩施州2021-2022学年高三上学期第一次教学质量监测数学试题辽宁省辽河油田第二高级中学2022-2023学年高三上学期期末考试数学试题江苏省南通市海安高级中学2021-2022学年高三上学期期中模拟数学试题湖北省宜昌市夷陵中学2021-2022学年高二上学期10月阶段性检测数学试题广东省广州市仲元中学2021-2022学年高二上学期期中数学试题重庆市万州第二高级中学2021-2022学年高二上学期期中数学试题山东省青岛市4区市2021-2022学年高二上学期期中考试数学试题重庆市第七中学校2021-2022学年高二上学期期中数学试题重庆市杨家坪中学2021-2022学年高二上学期第二次月考数学试题 福建省南平市浦城县2021-2022学年高二上学期期中考试数学试题福建省厦门第一中学2021-2022学年高二上学期期中考试数学试题(已下线)第33讲 立体几何中的范围与最值问题-2022年新高考数学二轮专题突破精练(已下线)考点35 立体几何中的综合问题-备战2022年高考数学典型试题解读与变式(已下线)专题35 立体几何中的探索性问题求解策略-学会解题之高三数学万能解题模板【2022版】(已下线)专题06 空间向量与立体几何(突破训练)-备战2022年高考数学二轮复习重难考点专项突破训练(全国通用)山东省枣庄市薛城区2021-2022学年高二上学期期末数学试题(已下线)专题23 立体几何中的压轴小题-2安徽省六安市舒城中学2022-2023学年高二上学期第二次月考数学试题福建省永安市第九中学2022-2023学年高二上学期9月月考数学试题
名校
10 . 如图,在棱长为6的正方体 中,
中, 为棱
为棱 上一点,且
上一点,且 为棱
为棱 的中点,点
的中点,点 是线段
是线段 上的动点,则( )
上的动点,则( )

 中,
中, 为棱
为棱 上一点,且
上一点,且 为棱
为棱 的中点,点
的中点,点 是线段
是线段 上的动点,则( )
上的动点,则( )
A.无论点 在线段 在线段 上如何移动,都有 上如何移动,都有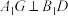 |
B.四面体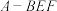 的体积为24 的体积为24 |
C.直线 与 与 所成角的余弦值为 所成角的余弦值为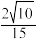 |
D.直线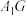 与平面 与平面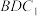 所成最大角的余弦值为 所成最大角的余弦值为 |
您最近一年使用:0次
2021-03-18更新
|
2582次组卷
|
9卷引用:辽宁省实验中学2022-2023学年高二实验班上学期期初测试数学试题
辽宁省实验中学2022-2023学年高二实验班上学期期初测试数学试题湖南省长沙市长郡中学2021-2022学年高二上学期入学考试数学试题九师联盟(湖北省)2021届高三下学期2月联考数学试题(已下线)专题20 立体几何角的计算问题(讲)-2021年高三数学二轮复习讲练测(新高考版)(已下线)专题24 立体几何角的计算问题(讲)-2021年高三数学二轮复习讲练测(文理通用)九师联盟(河北省)2021届高三下学期3月联考数学试题湖北省武汉市武钢三中2021-2022学年高二上学期10月月考数学试题苏教版(2019) 必修第二册 过关斩将 章节测试 第13章 立体几何初步湘鄂冀三省益阳平高学校、长沙市平高中学等七校2022-2023学年高二上学期10月联考数学试题



