已知抛物线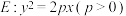 ,过点
,过点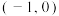 的两条直线
的两条直线 、
、 分别交
分别交 于
于 、
、 两点和
两点和 、
、 两点.当
两点.当 的斜率为
的斜率为 时,
时,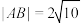 .
.
(1)求 的标准方程;
的标准方程;
(2)设 为直线
为直线 与
与 的交点,证明:点
的交点,证明:点 在定直线上.
在定直线上.
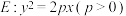 ,过点
,过点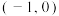 的两条直线
的两条直线 、
、 分别交
分别交 于
于 、
、 两点和
两点和 、
、 两点.当
两点.当 的斜率为
的斜率为 时,
时,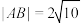 .
.(1)求
 的标准方程;
的标准方程;(2)设
 为直线
为直线 与
与 的交点,证明:点
的交点,证明:点 在定直线上.
在定直线上.
2023·山东·二模 查看更多[9]
山东省实验中学2023届高三第二次模拟考试数学试题黑龙江省大庆市萨尔图区第二十三中学2022-2023学年高二下学期期末数学试题(已下线)专题3.9 圆锥曲线中的定点、定值、定直线问题大题专项训练【九大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)考点17 解析几何中的定点与定直线问题 2024届高考数学考点总动员(已下线)重难点7-2 圆锥曲线综合应用(7题型+满分技巧+限时检测)(已下线)专题06 圆锥曲线大题(已下线)通关练17 抛物线8考点精练(3)(已下线)高二上学期期末考点大通关真题精选100题(3)(已下线)专题12 解析几何中的定直线问题【练】(压轴大全)
更新时间:2023/05/30 22:48:36
|
相似题推荐
解答题-问答题
|
较难
(0.4)
解题方法
【推荐1】已知抛物线C: 的焦点为F,过点P(2,0)作直线
的焦点为F,过点P(2,0)作直线 交抛物线于A,B两点.
交抛物线于A,B两点.
(1)若 的倾斜角为
的倾斜角为 ,求△FAB的面积;
,求△FAB的面积;
(2)过点A,B分别作抛物线C的两条切线 ,
, 且直线
且直线 与直线
与直线 相交于点M,问:点M是否在某定直线上?若在,求该定直线的方程,若不在,请说明理由.
相交于点M,问:点M是否在某定直线上?若在,求该定直线的方程,若不在,请说明理由.
 的焦点为F,过点P(2,0)作直线
的焦点为F,过点P(2,0)作直线 交抛物线于A,B两点.
交抛物线于A,B两点.(1)若
 的倾斜角为
的倾斜角为 ,求△FAB的面积;
,求△FAB的面积;(2)过点A,B分别作抛物线C的两条切线
 ,
, 且直线
且直线 与直线
与直线 相交于点M,问:点M是否在某定直线上?若在,求该定直线的方程,若不在,请说明理由.
相交于点M,问:点M是否在某定直线上?若在,求该定直线的方程,若不在,请说明理由.
您最近一年使用:0次
解答题-证明题
|
较难
(0.4)
解题方法
【推荐2】已知抛物线 :
: 的焦点为
的焦点为 ,直线
,直线 交抛物线于
交抛物线于 两点(
两点( 异于坐标原点
异于坐标原点 ),交
),交 轴于点
轴于点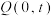 (
( ),且
),且 ,直线
,直线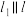 ,且与抛物线相切于点
,且与抛物线相切于点 .
.
(1)求证: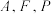 三点共线;
三点共线;
(2)过点 作该抛物线的切线
作该抛物线的切线 (点
(点 为切点),
为切点), 交
交 于点
于点 .
.
(ⅰ)试问,点 是否在定直线上,若在,请求出该直线,若不在,请说明理由;
是否在定直线上,若在,请求出该直线,若不在,请说明理由;
(ⅱ)求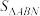 的最小值.
的最小值.
 :
: 的焦点为
的焦点为 ,直线
,直线 交抛物线于
交抛物线于 两点(
两点( 异于坐标原点
异于坐标原点 ),交
),交 轴于点
轴于点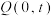 (
( ),且
),且 ,直线
,直线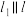 ,且与抛物线相切于点
,且与抛物线相切于点 .
.(1)求证:
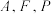 三点共线;
三点共线;(2)过点
 作该抛物线的切线
作该抛物线的切线 (点
(点 为切点),
为切点), 交
交 于点
于点 .
.(ⅰ)试问,点
 是否在定直线上,若在,请求出该直线,若不在,请说明理由;
是否在定直线上,若在,请求出该直线,若不在,请说明理由;(ⅱ)求
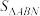 的最小值.
的最小值.
您最近一年使用:0次
解答题-证明题
|
较难
(0.4)
名校
解题方法
【推荐1】已知抛物线 的焦点为
的焦点为 ,过点
,过点 的直线
的直线 交拋物线
交拋物线 于
于 两点.
两点.
(1)当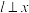 轴时,
轴时,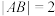 ,求抛物线
,求抛物线 的方程及焦点
的方程及焦点 的坐标;
的坐标;
(2)若直线 交
交 轴于点
轴于点 ,过点
,过点 且垂直于
且垂直于 轴的直线交抛物线
轴的直线交抛物线 于点
于点 ,直线
,直线 交抛物线
交抛物线 于另一点
于另一点 .
.
(i)是否存在定点 ,使得四边形
,使得四边形 为平行四边形?若存在,求出定点
为平行四边形?若存在,求出定点 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
(ii)求证: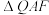 与
与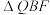 的面积之积为定值.
的面积之积为定值.
 的焦点为
的焦点为 ,过点
,过点 的直线
的直线 交拋物线
交拋物线 于
于 两点.
两点.(1)当
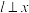 轴时,
轴时,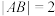 ,求抛物线
,求抛物线 的方程及焦点
的方程及焦点 的坐标;
的坐标;(2)若直线
 交
交 轴于点
轴于点 ,过点
,过点 且垂直于
且垂直于 轴的直线交抛物线
轴的直线交抛物线 于点
于点 ,直线
,直线 交抛物线
交抛物线 于另一点
于另一点 .
.(i)是否存在定点
 ,使得四边形
,使得四边形 为平行四边形?若存在,求出定点
为平行四边形?若存在,求出定点 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;(ii)求证:
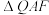 与
与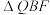 的面积之积为定值.
的面积之积为定值.
您最近一年使用:0次
解答题-证明题
|
较难
(0.4)
解题方法
【推荐2】已知抛物线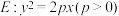 的焦点为F,过F且斜率为2的直线与E交于A,B两点,
的焦点为F,过F且斜率为2的直线与E交于A,B两点,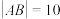 .
.
(1)求E的方程;
(2)直线 ,过l上一点P作E的两条切线
,过l上一点P作E的两条切线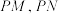 ,切点分别为M,N.求证:直线
,切点分别为M,N.求证:直线 过定点,并求出该定点坐标.
过定点,并求出该定点坐标.
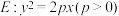 的焦点为F,过F且斜率为2的直线与E交于A,B两点,
的焦点为F,过F且斜率为2的直线与E交于A,B两点,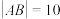 .
.(1)求E的方程;
(2)直线
 ,过l上一点P作E的两条切线
,过l上一点P作E的两条切线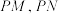 ,切点分别为M,N.求证:直线
,切点分别为M,N.求证:直线 过定点,并求出该定点坐标.
过定点,并求出该定点坐标.
您最近一年使用:0次

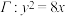 和圆
和圆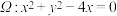 ,抛物线
,抛物线 的焦点为
的焦点为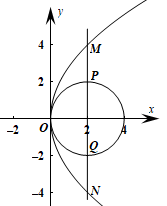
 的圆心到
的圆心到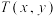 在抛物线
在抛物线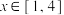 , 过点
, 过点 作圆
作圆 ,求四边形
,求四边形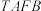 的面积的取值范围;
的面积的取值范围; 四点,证明:
四点,证明: 的充要条件是“直线
的充要条件是“直线 ”
”
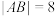 ,Q为抛物线上一点,过Q作两条均不垂直于对称轴的直线分别交抛物线于除Q之外的M、N两点.
,Q为抛物线上一点,过Q作两条均不垂直于对称轴的直线分别交抛物线于除Q之外的M、N两点. ,且
,且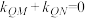 ,判断MN斜率是否为定值,若是,求出该值,若不是,说明理由.
,判断MN斜率是否为定值,若是,求出该值,若不是,说明理由.


