名校
解题方法
1 . 已知函数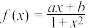 是定义在
是定义在 上的奇函数,且
上的奇函数,且 .
.
(1)求 的解析式;
的解析式;
(2)先判断函数 在
在 上的单调性,并证明;
上的单调性,并证明;
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 .
.(1)求
 的解析式;
的解析式;(2)先判断函数
 在
在 上的单调性,并证明;
上的单调性,并证明;
您最近一年使用:0次
2023-12-14更新
|
154次组卷
|
2卷引用:吉林省长春市第五中学2023-2024学年高一下学期期初考试数学试题
名校
2 . 求下列各式的值.
(1) ;
;
(2)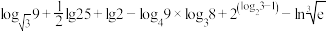 .
.
(1)
 ;
;(2)
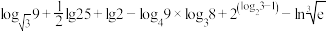 .
.
您最近一年使用:0次
解题方法
3 . 设函数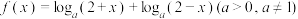 ,且
,且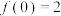 .
.
(1)求实数 的值及函数
的值及函数 的定义域;
的定义域;
(2)求函数 在区间
在区间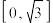 上的最小值.
上的最小值.
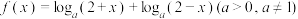 ,且
,且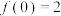 .
.(1)求实数
 的值及函数
的值及函数 的定义域;
的定义域;(2)求函数
 在区间
在区间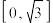 上的最小值.
上的最小值.
您最近一年使用:0次
4 . 对于任意给定的四个实数 ,
,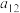 ,
,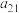 ,
,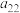 ,我们定义方阵
,我们定义方阵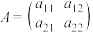 ,方阵
,方阵 对应的行列式记为
对应的行列式记为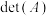 ,且
,且 ,方阵
,方阵 与任意方阵
与任意方阵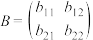 的乘法运算定义如下:
的乘法运算定义如下: ,其中方阵
,其中方阵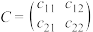 ,且
,且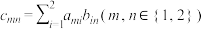 .设
.设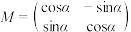 ,
,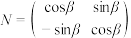 ,
, .
.
(1)证明: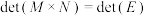 .
.
(2)若方阵 ,
, 满足
满足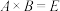 ,且
,且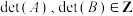 ,证明:
,证明: .
.
 ,
,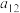 ,
,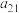 ,
,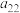 ,我们定义方阵
,我们定义方阵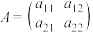 ,方阵
,方阵 对应的行列式记为
对应的行列式记为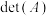 ,且
,且 ,方阵
,方阵 与任意方阵
与任意方阵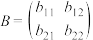 的乘法运算定义如下:
的乘法运算定义如下: ,其中方阵
,其中方阵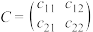 ,且
,且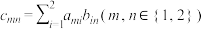 .设
.设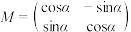 ,
,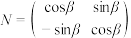 ,
, .
.(1)证明:
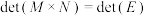 .
.(2)若方阵
 ,
, 满足
满足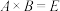 ,且
,且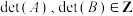 ,证明:
,证明: .
.
您最近一年使用:0次
2024-06-13更新
|
166次组卷
|
3卷引用:吉林省通化市梅河口市第五中学2024届高考模拟预测数学试题
名校
5 . 人类已经进入大数据时代.目前,数据量已经从TB(1TB=1024GB)级别跃升到PB(1PB=1024TB),EB(1EB=1024PB)乃至ZB(1ZB=1024EB)级别.国际数据公司(IDC)的研究结果表明,2008年起全球每年产生的数据量如下表所示:
年份 | 2008 | 2009 | 2010 | 2011 | … | 2020 |
数据量(ZB) | 0.49 | 0.8 | 1.2 | 1.82 | … | 80 |
(1)设2008年为第一年,为较好地描述2008年起第
 年全球生产的数据量
年全球生产的数据量 (单位:ZB)与
(单位:ZB)与 的关系,根据上述信息,试从
的关系,根据上述信息,试从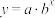 (
( ,
, 且
且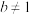 ),
), ,
, (
( ,
, 且
且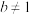 )三种函数模型中选择一个,应该选哪一个更合适?(不用说明理由);
)三种函数模型中选择一个,应该选哪一个更合适?(不用说明理由);(2)根据(1)中所选的函数模型,若选取2009年和2020年的数据量来估计模型中的参数,预计到哪一年,全球生产的数据量将达到2020年的100倍?
您最近一年使用:0次
2024-03-14更新
|
128次组卷
|
2卷引用:吉林省长春市东北师大附中2023-2024学年高一下学期寒假作业验收考试数学试卷
名校
解题方法
6 . 已知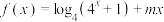 是偶函数.
是偶函数.
(1)求 的值;
的值;
(2)已知不等式 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
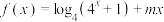 是偶函数.
是偶函数.(1)求
 的值;
的值;(2)已知不等式
 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2018-04-03更新
|
1539次组卷
|
3卷引用:吉林省长春市外国语学校2023-2024学年高一下学期期初考试数学试题
吉林省长春市外国语学校2023-2024学年高一下学期期初考试数学试题北京市北京十一学校2017-2018学年高一数ⅢA期末数学试题(已下线)第06章 幂函数、指数函数和对数函数(A卷基础篇)-2020-2021学年高一数学必修第一册同步单元AB卷(新教材苏教版)
名校
解题方法
7 . 已知函数 满足
满足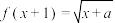 ,且
,且 .
.
(1)求 的值和函数
的值和函数 的解析式;
的解析式;
(2)判断 在其定义域的单调性并加以证明.
在其定义域的单调性并加以证明.
 满足
满足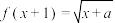 ,且
,且 .
.(1)求
 的值和函数
的值和函数 的解析式;
的解析式;(2)判断
 在其定义域的单调性并加以证明.
在其定义域的单调性并加以证明.
您最近一年使用:0次
2022-01-12更新
|
274次组卷
|
2卷引用:吉林省长春市第二实验中学2023-2024学年高一下学期开学考试数学试题
名校
8 . 心理学家根据高中生心理发展规律,对高中生的学习行为进行研究,发现学生学习的接受能力依赖于老师引入概念和描述问题所用的时间.上课开始时,学生的兴趣激增,中间有一段时间学生的兴趣保持理想状态,随后学生的注意力开始分散.分析结果和实验表明,用 表示学生掌握和接受概念的能力(
表示学生掌握和接受概念的能力( 的值越大,表示接受能力越强),x表示提出和讲授概念的时间(单位:
的值越大,表示接受能力越强),x表示提出和讲授概念的时间(单位: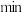 ),满足以下关系:
),满足以下关系:
(1)上课多少分钟后,学生的接受能力最强?能维持多少分钟?
(2)有一道数学难题,需要54的接受能力及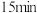 的讲授时间,老师能否及时在学生处于所需接受能力的状态下讲授完成这道难题?
的讲授时间,老师能否及时在学生处于所需接受能力的状态下讲授完成这道难题?
 表示学生掌握和接受概念的能力(
表示学生掌握和接受概念的能力( 的值越大,表示接受能力越强),x表示提出和讲授概念的时间(单位:
的值越大,表示接受能力越强),x表示提出和讲授概念的时间(单位: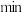 ),满足以下关系:
),满足以下关系:
(1)上课多少分钟后,学生的接受能力最强?能维持多少分钟?
(2)有一道数学难题,需要54的接受能力及
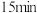 的讲授时间,老师能否及时在学生处于所需接受能力的状态下讲授完成这道难题?
的讲授时间,老师能否及时在学生处于所需接受能力的状态下讲授完成这道难题?
您最近一年使用:0次
2024-01-21更新
|
117次组卷
|
2卷引用:吉林省四校2023-2024学年高一下学期期初联考数学试题
9 . 不用计算器求下列各式的值
(1)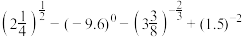 ;
;
(2)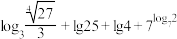 .
.
(1)
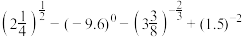 ;
;(2)
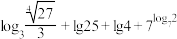 .
.
您最近一年使用:0次
2020-07-28更新
|
600次组卷
|
10卷引用:吉林省长春市外国语学校2023-2024学年高一下学期期初考试数学试题
吉林省长春市外国语学校2023-2024学年高一下学期期初考试数学试题河北省承德一中2017-2018学年高一上学期第三次月考数学试卷【全国百强校】广东省广州市荔湾区广雅中学2016-2017学年高一上学期期中考试数学试题【校级联考】福建省闽侯二中五校教学联合体2017-2018学年高一上学期期中考试数学试题【市级联考】安徽省天长市2018-2019学年高一上学期期末统考数学试题贵州省六盘水市第二中学2019—2020学年度高一上学期期中数学试题广西南宁市第三中学2019-2020学年高一上学期期中数学试题福建省福州福清市2017-2018学年学年高一上学期期中考试数学试题福建省永安市第一中学2021届高三上学期第一次月考数学试题陕西省咸阳市武功县2021-2022学年高一上学期期中数学试题
名校
10 . 已知函数 (
( 且
且 )在
)在 上的最大值与最小值之差为
上的最大值与最小值之差为
(1)求实数 的值;
的值;
(2)若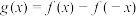 ,当
,当 时,解不等式
时,解不等式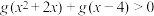 .
.
 (
( 且
且 )在
)在 上的最大值与最小值之差为
上的最大值与最小值之差为
(1)求实数
 的值;
的值;(2)若
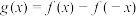 ,当
,当 时,解不等式
时,解不等式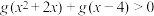 .
.
您最近一年使用:0次



