名校
解题方法
1 . 近年来,网络消费新业态、新应用不断涌现,消费场景也随之加速拓展,某报社开展了网络交易消费者满意度调查,某县人口约为50万人,从该县随机选取5000人进行问卷调查,根据满意度得分分成以下5组: 、
、 、
、 、
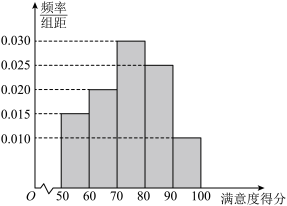
、 ,统计结果如图所示.由频率分布直方图可认为满意度得分X(单位:分)近似地服从正态分布
,统计结果如图所示.由频率分布直方图可认为满意度得分X(单位:分)近似地服从正态分布 ,且
,且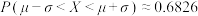 ,
,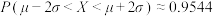 ,
,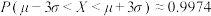 ,其中
,其中 近似为样本平均数,
近似为样本平均数, 近似为样本的标准差s,并已求得
近似为样本的标准差s,并已求得 .则以下不正确的是( )
.则以下不正确的是( )
 、
、 、
、 、
、 ,统计结果如图所示.由频率分布直方图可认为满意度得分X(单位:分)近似地服从正态分布
,统计结果如图所示.由频率分布直方图可认为满意度得分X(单位:分)近似地服从正态分布 ,且
,且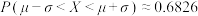 ,
,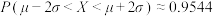 ,
,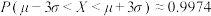 ,其中
,其中 近似为样本平均数,
近似为样本平均数, 近似为样本的标准差s,并已求得
近似为样本的标准差s,并已求得 .则以下不正确的是( )
.则以下不正确的是( )
| A.由直方图可估计样本的平均数约为74.5 |
| B.由直方图可估计样本的中位数约为75 |
C.由正态分布估计全县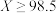 的人数约为2.3万人 的人数约为2.3万人 |
D.由正态分布估计全县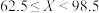 的人数约为40.9万人 的人数约为40.9万人 |
您最近一年使用:0次
名校
解题方法
2 . 4月23日是世界读书日,树人中学为了解本校学生课外阅读情况,按性别进行分层,用分层随机抽样的方法从全校学生中抽出一个容量为100的样本,其中男生40名,女生60名经调查统计,分别得到40名男生一周课外阅读时间(单位,小时)的频数分布表和60名女生一周课外阅读时间(单位:小时)的频率分布直方图:(以各组的区间中点值代表该组的各个值)女生一周自读时间频率分布直方图
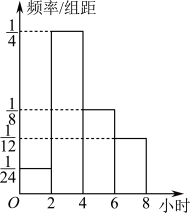
(1)从一周课外阅读时间为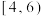 的学生中按比例分配抽取6人,则男生,女生各抽出多少人?
的学生中按比例分配抽取6人,则男生,女生各抽出多少人?
(2)分别估计男生和女生一周课外阅读时间的平均数 ;
;
(3)估计总样本的平均数 和方差
和方差 .
.
参考数据和公式;男生和女生一周课外阅读时间方差的估计值分别为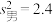 和
和 .
.
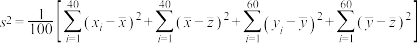 ,
,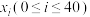 和
和 分别表示男生和女生一周阅读时间的样本,其中
分别表示男生和女生一周阅读时间的样本,其中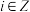 .
.
| 男生一周阅读时间频数分布表 | |
| 小时 | 频数 |
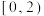 | 9 |
 | 25 |
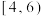 | 3 |
 | 3 |

(1)从一周课外阅读时间为
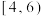 的学生中按比例分配抽取6人,则男生,女生各抽出多少人?
的学生中按比例分配抽取6人,则男生,女生各抽出多少人?(2)分别估计男生和女生一周课外阅读时间的平均数
 ;
;(3)估计总样本的平均数
 和方差
和方差 .
.参考数据和公式;男生和女生一周课外阅读时间方差的估计值分别为
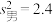 和
和 .
.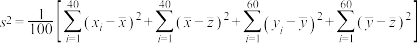 ,
,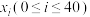 和
和 分别表示男生和女生一周阅读时间的样本,其中
分别表示男生和女生一周阅读时间的样本,其中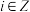 .
.
您最近一年使用:0次
2023-06-11更新
|
1082次组卷
|
8卷引用:吉林省通化市梅河口市第五中学2022-2023学年高一下学期期末数学试题
吉林省通化市梅河口市第五中学2022-2023学年高一下学期期末数学试题(已下线)第10章 概率 章末测试(提升)-一隅三反系列(人教A版2019必修第二册)广东省广州市天河中学2022-2023学年高一下学期期中数学试题江苏省盐城市响水中学2022-2023学年高一下学期期末模拟数学试题(已下线)模块三 专题8 (统计与概率)(拔高能力练)(人教A版)(已下线)模块三 专题9 大题分类连(统计与概率)(拔高能力练)(苏教版)广东省东莞市2020-2021学年高一下学期期末数学试题(已下线)第十章 概率 章末测试(提升)-2021-2022学年高一数学一隅三反系列(人教A版2019必修第二册)
名校
解题方法
3 . 为了提高学生的英语基础,某中学要求学生每天坚持一小时的听、说、读、写训练.为了调查该校5000名高中学生每周平均参加英语训练时间的情况,某教师从高一、高二、高三三个年级学生中按照3∶1∶1的比例分层抽样,收集了100名学生平均每周英语训练时间的样本数据(单位:h),整理后得到如图所示的频率分布直方图,则下列说法中正确的有( )
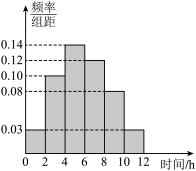

| A.估计该校高中学生平均每周英语训练时间不足4h的人数为1500人 |
| B.估计该校高中学生平均每周英语训练时间不少于8h的人数所占百分比为22% |
| C.估计该校高中学生平均每周英语训练时间的中位数为5h |
| D.估计该校高中学生平均每周英语训练时间为5.84h |
您最近一年使用:0次
名校
解题方法
4 . 某公司为了让职工业余时间加强体育锻炼,修建了一个运动俱乐部,公司随机抽查了200名职工在修建运动俱乐部前后每天运动的时间,得到以下频数分布表:
表一(运动俱乐部修建前)
表二(运动俱乐部修建后)
(1)分别求出修建运动俱乐部前和修建运动俱乐部后职工每天运动的平均时间(同一时间段的数据取该组区间的中点值作代表)﹔
(2)运动俱乐部内有一套与室温调节有关的设备,内有2个完全一样的用电器A,只有这2个用电器A都正常工作时,整套设备才正常工作,且2个用电器A是否正常工作互不影响.用电器A有M,N两种品牌,M品牌的销售单价为1000元,正常工作寿命为11个月或12个月(概率均为 );N品牌的销售单价为400元,正常工作寿命为5个月或6个月(概率均为
);N品牌的销售单价为400元,正常工作寿命为5个月或6个月(概率均为 ).现有两种购置方案:
).现有两种购置方案:
方案1:购置2个M品牌用电器﹔
方案2:购置1个M品牌用电器和2个N品牌用电器(其中1个N品牌用电器不能正常工作时则使用另一个N品牌用电器).
试求两种方案各自设备性价比(设备正常运行时间与购置用电器A的成本比)的分布列,并从性价比的数学期望角度考虑,选择哪种方案更实惠?
表一(运动俱乐部修建前)
| 时间(分钟) |  |  | 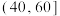 | 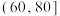 |
| 人数 | 36 | 58 | 81 | 25 |
| 时间(分钟) |  |  | 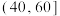 | 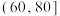 |
| 人数 | 18 | 63 | 83 | 36 |
(2)运动俱乐部内有一套与室温调节有关的设备,内有2个完全一样的用电器A,只有这2个用电器A都正常工作时,整套设备才正常工作,且2个用电器A是否正常工作互不影响.用电器A有M,N两种品牌,M品牌的销售单价为1000元,正常工作寿命为11个月或12个月(概率均为
 );N品牌的销售单价为400元,正常工作寿命为5个月或6个月(概率均为
);N品牌的销售单价为400元,正常工作寿命为5个月或6个月(概率均为 ).现有两种购置方案:
).现有两种购置方案:方案1:购置2个M品牌用电器﹔
方案2:购置1个M品牌用电器和2个N品牌用电器(其中1个N品牌用电器不能正常工作时则使用另一个N品牌用电器).
试求两种方案各自设备性价比(设备正常运行时间与购置用电器A的成本比)的分布列,并从性价比的数学期望角度考虑,选择哪种方案更实惠?
您最近一年使用:0次
2023-05-19更新
|
525次组卷
|
5卷引用:吉林省白山市抚松县第一中学2022-2023学年高三第十一次校内模拟数学试题
名校
5 . 某校为了解高一学生在五一假期中参加社会实践活动的情况,抽样调查了其中的100名学生,统计他们参加社会实践活动的时间(单位:小时),并将统计数据绘制成如图的频率分布直方图.
(2)估计这100名学生在这个五一假期中参加社会实践活动的时间的75百分位数(结果保留两位小数).
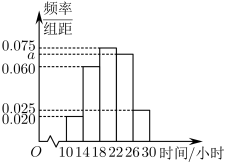
(2)估计这100名学生在这个五一假期中参加社会实践活动的时间的75百分位数(结果保留两位小数).
您最近一年使用:0次
2023-05-12更新
|
4121次组卷
|
13卷引用:吉林省普通高中友好学校联合体2022-2023学年高一下学期第三十六届基础年段期末联考数学试题
吉林省普通高中友好学校联合体2022-2023学年高一下学期第三十六届基础年段期末联考数学试题浙江省长河高级中学2022-2023学年高一下学期期中数学试题(已下线)14.4 用样本估计总体 (1) -《考点·题型·技巧》第十四章 统计(B卷·能力提升练)-【单元测试】(已下线)统计专题:四种统计图的应用-【题型分类归纳】(已下线)高一下学期数学期末押题卷01-期末高分必刷题型天津市宝坻第一中学2022-2023学年高一下学期阶段练习四数学试题(已下线)期末专题06 统计综合-【备战期末必刷真题】广东省东莞市东莞中学2022-2023学年高一下学期期中考试数学试题河北省邯郸市鸡泽县第一中学2023-2024学年高二上学期开学考数学试题浙江省绍兴市2021-2022学年高一下学期期末数学试题单元测试A卷——第九章?统计(已下线)第14章 统计 单元综合检测(重难点)-《重难点题型·高分突破》(苏教版2019必修第二册)
名校
6 . 我国是世界上严重缺水的国家之一,为提倡节约用水,我市为了制定合理的节水方案,对家庭用水情况进行了调查,通过抽样,获得了2021年 100个家庭的月均用水量(单位:t),将数据按照[0,2),[2,4),[4,6),[6,8),[8,10]分成5组,制成了如图所示的频率分布直方图.
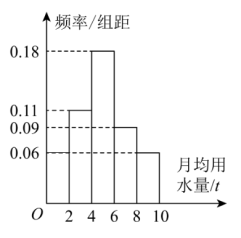
(1)求全市家庭月均用水量不低于 6t的频率;
(2)假设同组中的每个数据都用该组区间的中点值代替,求全市家庭月均用水量平均数的估计值;
(3)求全市家庭月均用水量的75%分位数的估计值(精确到0.01).

(1)求全市家庭月均用水量不低于 6t的频率;
(2)假设同组中的每个数据都用该组区间的中点值代替,求全市家庭月均用水量平均数的估计值;
(3)求全市家庭月均用水量的75%分位数的估计值(精确到0.01).
您最近一年使用:0次
2023-05-05更新
|
2695次组卷
|
6卷引用:吉林省长春市长春外国语学校2022-2023学年高一下学期期末数学试题
吉林省长春市长春外国语学校2022-2023学年高一下学期期末数学试题第十四章 统计(A卷·基础提升练)(已下线)9.2 用样本估计总体(精讲)-【题型分类归纳】(已下线)专题13 统计-期中期末考点大串讲(苏教版2019必修第二册)四川省南充市嘉陵第一中学2022-2023学年高一下学期第三次月考(6月)数学试题江苏省无锡市辅仁高级中学2021-2022学年高一下学期期末数学试题
7 . 某精密检测仪器厂锐意改革,实施科学化、精细化管理,产量大幅提高.产品制成后先去掉残次品,然后随机按每箱 件装箱.现从中随机抽取
件装箱.现从中随机抽取 箱,测得其内径(单位:cm),将结果分成
箱,测得其内径(单位:cm),将结果分成 组:
组: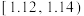 ,
,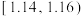 ,
, ,
,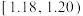 ,并绘制出如图所示的频率分布直方图.
,并绘制出如图所示的频率分布直方图.
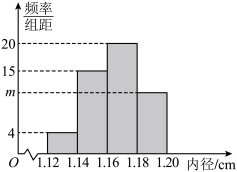
(1)估计这批产品每件内径的平均值 (残次品除外,同一组中的数据以这组数据所在区间中点的值为代表);
(残次品除外,同一组中的数据以这组数据所在区间中点的值为代表);
(2)若这批产品每件内径 服从正态分布
服从正态分布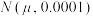 ,其中
,其中 的近似值为产品每件内径的平均值
的近似值为产品每件内径的平均值 ,请估计
,请估计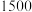 箱产品中内径位于
箱产品中内径位于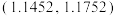 内产品的件数;
内产品的件数;
(3)规定这批产品中内径位于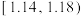 内的产品为优质品,视频率为概率,随机打开一箱,记优质品的件数为
内的产品为优质品,视频率为概率,随机打开一箱,记优质品的件数为 ,求
,求 的数学期望.
的数学期望.
附:若随机变量 ,则
,则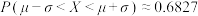 ,
,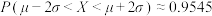 .
.
 件装箱.现从中随机抽取
件装箱.现从中随机抽取 箱,测得其内径(单位:cm),将结果分成
箱,测得其内径(单位:cm),将结果分成 组:
组: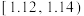 ,
,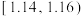 ,
, ,
,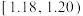 ,并绘制出如图所示的频率分布直方图.
,并绘制出如图所示的频率分布直方图.
(1)估计这批产品每件内径的平均值
 (残次品除外,同一组中的数据以这组数据所在区间中点的值为代表);
(残次品除外,同一组中的数据以这组数据所在区间中点的值为代表);(2)若这批产品每件内径
 服从正态分布
服从正态分布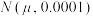 ,其中
,其中 的近似值为产品每件内径的平均值
的近似值为产品每件内径的平均值 ,请估计
,请估计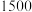 箱产品中内径位于
箱产品中内径位于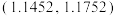 内产品的件数;
内产品的件数;(3)规定这批产品中内径位于
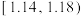 内的产品为优质品,视频率为概率,随机打开一箱,记优质品的件数为
内的产品为优质品,视频率为概率,随机打开一箱,记优质品的件数为 ,求
,求 的数学期望.
的数学期望.附:若随机变量
 ,则
,则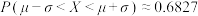 ,
,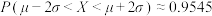 .
.
您最近一年使用:0次
名校
解题方法
8 . 某市为了传承发展中华优秀传统文化,组织该市中学生进行了一次文化知识有奖竞赛,竞赛奖励规则如下,得分在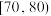 内的学生获三等奖,得分在
内的学生获三等奖,得分在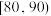 内的学生获二等奖,得分在
内的学生获二等奖,得分在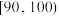 内的学生获一等奖,其他学生不得奖.为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,并以此为样本绘制了如下样本频率分布直方图.
内的学生获一等奖,其他学生不得奖.为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,并以此为样本绘制了如下样本频率分布直方图.
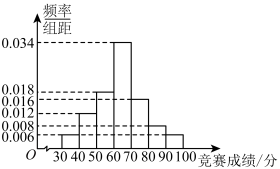
(1)现从该样本中随机抽取两名学生的竞赛成绩,求这两名学生中恰有一名学生获奖的概率;
(2)若该市所有参赛学生的成绩X近似服从正态分布 ,其中
,其中 ,
, 为样本平均数的估计值,利用所得正态分布模型解决以下问题:
为样本平均数的估计值,利用所得正态分布模型解决以下问题:
①若该市共有10000名学生参加了竞赛,试估计参赛学生中成绩超过79分的学生数(结果四舍五入到整数);
②若从所有参赛学生中(参赛学生数大于10000)随机抽取4名学生进行访谈,求其中竞赛成绩在64分以上的学生人数的期望与方差.
附参考数据:若随机变量X服从正态分布 ,则
,则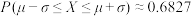 ,
,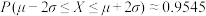 ,
,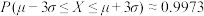 .
.
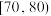 内的学生获三等奖,得分在
内的学生获三等奖,得分在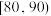 内的学生获二等奖,得分在
内的学生获二等奖,得分在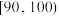 内的学生获一等奖,其他学生不得奖.为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,并以此为样本绘制了如下样本频率分布直方图.
内的学生获一等奖,其他学生不得奖.为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,并以此为样本绘制了如下样本频率分布直方图.
(1)现从该样本中随机抽取两名学生的竞赛成绩,求这两名学生中恰有一名学生获奖的概率;
(2)若该市所有参赛学生的成绩X近似服从正态分布
 ,其中
,其中 ,
, 为样本平均数的估计值,利用所得正态分布模型解决以下问题:
为样本平均数的估计值,利用所得正态分布模型解决以下问题:①若该市共有10000名学生参加了竞赛,试估计参赛学生中成绩超过79分的学生数(结果四舍五入到整数);
②若从所有参赛学生中(参赛学生数大于10000)随机抽取4名学生进行访谈,求其中竞赛成绩在64分以上的学生人数的期望与方差.
附参考数据:若随机变量X服从正态分布
 ,则
,则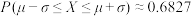 ,
,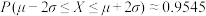 ,
,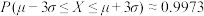 .
.
您最近一年使用:0次
2023-04-13更新
|
1007次组卷
|
2卷引用:吉林省长春市实验中学2022-2023学年高二下学期期中数学试题
9 . 某国家网球队为了预选2024年奥运会的参赛选手,预计在国家队选拔一批队员做特训.选拔过程中,记录了某队员的40局接球成绩,每局发100个球,该队员每接球成功得1分,否则得0分,且每局结果相互独立,得到如图所示的频率分布直方图.
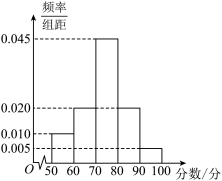
(1)结合直方图,估算该队员40局接球成绩的平均分(同一组数据用该组区间的中点值作代表);
(2)若该队员的接球训练成绩X近似服从正态分布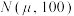 ,其中
,其中 近似为样本平均数,求
近似为样本平均数,求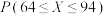 的值;
的值;
(3)为了营造竞技氛围,队员间相互比赛.一局比赛中发球方连续发100个球,若接球方得分达到80分,则接球方获胜,否则发球方获胜.若有人获胜达3局,则比赛结束,记比赛的局数为Y.以频率分布直方图中该队员获胜的频率作为概率,求均值 .
.
参考数据:若随机变量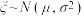 ,则
,则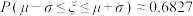 ,
,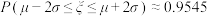 ,
, .
.

(1)结合直方图,估算该队员40局接球成绩的平均分(同一组数据用该组区间的中点值作代表);
(2)若该队员的接球训练成绩X近似服从正态分布
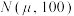 ,其中
,其中 近似为样本平均数,求
近似为样本平均数,求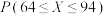 的值;
的值;(3)为了营造竞技氛围,队员间相互比赛.一局比赛中发球方连续发100个球,若接球方得分达到80分,则接球方获胜,否则发球方获胜.若有人获胜达3局,则比赛结束,记比赛的局数为Y.以频率分布直方图中该队员获胜的频率作为概率,求均值
 .
.参考数据:若随机变量
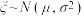 ,则
,则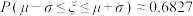 ,
,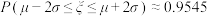 ,
, .
.
您最近一年使用:0次
2023-03-23更新
|
873次组卷
|
2卷引用:吉林省通化市梅河口市第五中学2023届高考二模考试数学试题(火箭班)
名校
解题方法
10 . 近年来、新冠疫情波及到千家万户,人们的生活方式和习惯不得不发生转变,短视频成了观众空闲时娱乐活动的首选.某电影艺术中心为了解短视频平台的观众年龄分布情况,向各大短视频平台的观众发放了线上调查问卷,共回收有效样本4000份,根据所得信息制作了如图所示的频率分布直方图,则下列说法正确的是( )
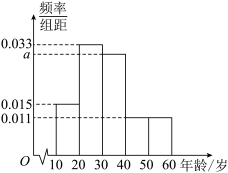

A.图中 |
| B.在4000份有效样本中,短视频观众年龄在10~20岁的有1320人 |
| C.估计短视频观众的平均年龄为32岁 |
| D.估计短视频观众年龄的75%分位数为39岁 |
您最近一年使用:0次
2023-01-10更新
|
317次组卷
|
3卷引用:吉林省梅河口市第五中学2023-2024学年高三上学期开学数学试题



