1 . 某医科大学科研部门为研究退休人员是否患痴呆症与上网的关系,随机调查了 市100位退休人员,统计数据如下表所示:
市100位退休人员,统计数据如下表所示:
患痴呆症 | 不患痴呆症 | 合计 | |
上网 | 16 | 32 | 48 |
不上网 | 34 | 18 | 52 |
合计 | 50 | 50 | 100 |
(1)依据
 的独立性检验,能否认为该市退休人员是否患痴呆症与上网之间有关联?
的独立性检验,能否认为该市退休人员是否患痴呆症与上网之间有关联?(2)从该市退休人员中任取一位,记事件A为“此人患痴呆症”,
 为“此人上网”,则
为“此人上网”,则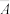 为“此人不患痴呆症”,定义事件A的强度
为“此人不患痴呆症”,定义事件A的强度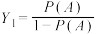 ,在事件
,在事件 发生的条件下A的强度
发生的条件下A的强度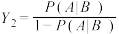 .
.(i)证明: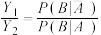 ;
;
(ⅱ)利用抽样的样本数据,估计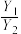 的值.
的值.
附: ,其中
,其中 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(1)一个兴趣小组发现,来自不同的城市的游客选择出行的习惯会有很大差异,为了验证这一猜想该小组进行了研究.请完成下列
 列联表,并根据小概率值
列联表,并根据小概率值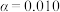 的独立性检验,分析城市规模是否与出行偏好地铁有关?(精确到0.001)
的独立性检验,分析城市规模是否与出行偏好地铁有关?(精确到0.001)单位:人
出行方式 | 国际大都市 | 中小型城市 | 合计 |
偏好地铁 | 20 | 100 | |
偏好其他 | 60 | ||
合计 | 60 |
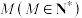 段,为了更好的体验文化,相邻两段的出行方式不能相同,且选择地铁、公交、打车、共享单车的概率是等可能的.已知他每日从酒店出行的方式一定是从地铁开始,记第
段,为了更好的体验文化,相邻两段的出行方式不能相同,且选择地铁、公交、打车、共享单车的概率是等可能的.已知他每日从酒店出行的方式一定是从地铁开始,记第 段行程上David坐地铁的概率为
段行程上David坐地铁的概率为 ,易知
,易知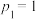 ,
,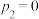
①试证明
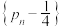 为等比数列;
为等比数列;②设第
 次David选择共享单车的概率为
次David选择共享单车的概率为 ,比较
,比较 与
与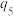 的大小.
的大小.附:
 ,
, .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
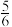 ,女性患Ⅰ型病的人数占女性病人的
,女性患Ⅰ型病的人数占女性病人的 .
.(1)若依据小概率值
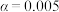 的独立性检验,认为“所患疾病类型”与“性别”有关,求男性患者至少有多少人?
的独立性检验,认为“所患疾病类型”与“性别”有关,求男性患者至少有多少人?(2)某药品研发公司欲安排甲乙两个研发团队来研发此疾病的治疗药物.两个团队各至多排2个接种周期进行试验.甲团队研发的药物每次接种后产生抗体的概率为
 ,每人每次接种花费
,每人每次接种花费 元,每个周期至多接种3次,第一个周期连续2次出现抗体测终止本接种周期进入第二个接种周期,否则需依次接种至第一周期结束,再进入第二周期:第二接种周期连续2次出现抗体则终止试验,否则依次接种至至试验结束:乙团队研发的药物每次接种后产生抗体概率为
元,每个周期至多接种3次,第一个周期连续2次出现抗体测终止本接种周期进入第二个接种周期,否则需依次接种至第一周期结束,再进入第二周期:第二接种周期连续2次出现抗体则终止试验,否则依次接种至至试验结束:乙团队研发的药物每次接种后产生抗体概率为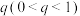 ,每人每次花费
,每人每次花费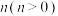 元,每个周期接种3次,每个周期必须完成3次接种,若一个周期内至少出现2次抗体,则该周期结束后终止试验,否则进入第二个接种周期、假设两个研发团队每次接种后产生抗体与否均相互独立.当
元,每个周期接种3次,每个周期必须完成3次接种,若一个周期内至少出现2次抗体,则该周期结束后终止试验,否则进入第二个接种周期、假设两个研发团队每次接种后产生抗体与否均相互独立.当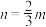 ,
, 时,从两个团队试验的平均花费考虑,试证明该公司选择乙团队进行药品研发的决策是正确的.
时,从两个团队试验的平均花费考虑,试证明该公司选择乙团队进行药品研发的决策是正确的.参考公式:
 (其中
(其中 为样本容量)
为样本容量)参考数据:
α | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.897 | 10.828 |
发病 | 没发病 | 合计 | |
接种疫苗 | 8 | 16 | 24 |
没接种疫苗 | 17 | 9 | 26 |
合计 | 25 | 25 | 50 |
(2)从该地区此动物群中任取一只,记
 表示此动物发病,
表示此动物发病,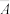 表示此动物没发病,
表示此动物没发病, 表示此动物接种疫苗,定义事件
表示此动物接种疫苗,定义事件 的优势
的优势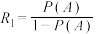 ,在事件
,在事件 发生的条件下
发生的条件下 的优势
的优势 .
.(ⅰ)证明:
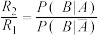 ;
;(ⅱ)利用抽样的样本数据,给出
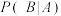 ,
,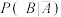 的估计值,并给出
的估计值,并给出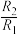 的估计值.附:
的估计值.附: ,其中
,其中 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
 ,
, 两个品种的蜜蜂各120只进行研究,得到如下数据:
两个品种的蜜蜂各120只进行研究,得到如下数据:| 黄色蜂蜡罐 | 褐色蜂蜡罐 | |
 品种蜜蜂 品种蜜蜂 | 80 | 40 |
 品种蜜蜂 品种蜜蜂 | 100 | 20 |
 的独立性检验,分析认为蜜蜂进入不同颜色的蜂蜡罐与蜜蜂种类有关联?
的独立性检验,分析认为蜜蜂进入不同颜色的蜂蜡罐与蜜蜂种类有关联?(2)假设要计算某事件的概率
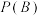 ,常用的一个方法就是找一个与
,常用的一个方法就是找一个与 事件有关的事件
事件有关的事件 ,利用公式:
,利用公式: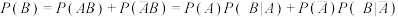 求解.现从装有
求解.现从装有 只
只 品种蜜蜂和
品种蜜蜂和 只
只 品种蜜蜂的蜂蜡罐中不放回地任意抽取两只,令第一次抽到
品种蜜蜂的蜂蜡罐中不放回地任意抽取两只,令第一次抽到 品种蜜蜂为事件
品种蜜蜂为事件 ,第二次抽到
,第二次抽到 品种蜜蜂为事件
品种蜜蜂为事件 .
.(ⅰ)证明:
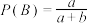 ;
;(ⅱ)研究发现,①
 品种蜜蜂飞入黄色蜂蜡罐概率为
品种蜜蜂飞入黄色蜂蜡罐概率为 ,被抽到的概率为
,被抽到的概率为 ;
; 品种蜜蜂飞入褐色蜂蜡罐概率为
品种蜜蜂飞入褐色蜂蜡罐概率为 ,被抽到的概率为
,被抽到的概率为 ;②
;② 品种蜜蜂飞入黄色蜂蜡罐概率为
品种蜜蜂飞入黄色蜂蜡罐概率为 ,被抽到的概率为
,被抽到的概率为 ;
; 品种蜜蜂飞入褐色蜂蜡罐概率为
品种蜜蜂飞入褐色蜂蜡罐概率为 ,被抽到的概率为
,被抽到的概率为 .请从
.请从 ,
, 两个品种蜜蜂中选择一种,求该品种蜜蜂被抽到的概率.
两个品种蜜蜂中选择一种,求该品种蜜蜂被抽到的概率.
| 男 | 女 | 合计 | |
| 喜爱 | 30 | 40 | |
| 不喜爱 | 40 | 60 | |
| 合计 | 50 | 100 |
(2)从观众中任选一人,A表示事件“选中的观众为男性”,B表示事件“不喜欢篮球运动”.
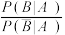 与
与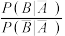 的比值是性别对运动热爱程度的一项度量指标,记该指标为R.
的比值是性别对运动热爱程度的一项度量指标,记该指标为R.①证明:
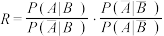 ;
;②利用男观众的数据统计,给出
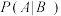 ,
, 的估计值,并求出R的估计值.
的估计值,并求出R的估计值.附:
 ,其中
,其中 .
.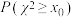 | 0.010 | 0.005 | 0.001 |
 | 6.635 | 7.879 | 10.828 |
性别 | 身高 | 合计 | |
低于170cm | 高于170cm | ||
女 | 14 | 7 | 21 |
男 | 8 | 11 | 19 |
合计 | 22 | 18 | 40 |
附:
 ,n=a+b+c+d
,n=a+b+c+dα | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
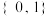 的成对分类变量,已知
的成对分类变量,已知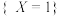 和
和 ,
, 和
和 都是互为对立事件.令
都是互为对立事件.令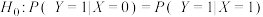 为零假设或原假设.证明:若零假设成立,则
为零假设或原假设.证明:若零假设成立,则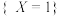 和
和 独立.
独立.
 .
.经常喝酒 | 不经常喝酒 | |
患糖尿病 | 4 | |
没患糖尿病 | 6 |
 列联表,依据小概率值
列联表,依据小概率值 的独立性检验,判断当地成年男性患糖尿病是否和喝酒习惯有关联?
的独立性检验,判断当地成年男性患糖尿病是否和喝酒习惯有关联?(2)从该地任选一人,
 表示事件“选到的人经常喝酒”,
表示事件“选到的人经常喝酒”, 表示事件“选到的人患糖尿病”,把
表示事件“选到的人患糖尿病”,把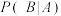 与
与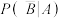 的比值叫“常喝酒和患糖尿病的关联指数”,记为
的比值叫“常喝酒和患糖尿病的关联指数”,记为 .
.(ⅰ)利用该调查数据求
 的值;
的值;(ⅱ)证明:
 .
.参考公式及数表:
 ,
,
| 0.15 | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
9 . 2022年11月20日,卡塔尔足球世界杯正式开幕,世界杯上的中国元素随处可见.从体育场建设到电力保障,从赛场内的裁判到赛场外的吉祥物都是中国制造,为卡塔尔世界杯提供了强有力的支持.国内也再次掀起足球热潮.某地足球协会组建球队参加业余比赛,该足球队教练组为了考查球员甲对球队的贡献,作出如下数据统计(甲参加过的比赛均分出了输赢):
球队输球 | 球队赢球 | 总计 | |
甲参加 | 2 | 30 | 32 |
甲未参加 | 8 | 10 | 18 |
总计 | 10 | 40 | 50 |
(1)根据小概率值
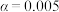 的独立性检验,能否认为该球队赢球与甲球员参赛有关联;
的独立性检验,能否认为该球队赢球与甲球员参赛有关联;(2)从该球队中任选一人,A表示事件“选中的球员参赛”,B表示事件“球队输球”.
 与
与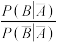 的比值是选中的球员参赛对球队贡献程度的一项度量指标,记该指标为R.
的比值是选中的球员参赛对球队贡献程度的一项度量指标,记该指标为R.①证明: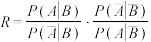 ;
;
②利用球员甲数据统计,给出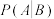 ,
,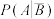 的估计值,并求出R的估计值.
的估计值,并求出R的估计值.
附: .
.
参考数据:
a | 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
不够良好 | 良好 | |
病例组 | 40 | 60 |
对照组 | 10 | 90 |
(2)从该地的人群中任选一人,A表示事件“选到的人卫生习惯不够良好”,B表示事件“选到的人患有该疾病”.
 与
与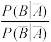 的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为R.
的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为R.(ⅰ)证明:
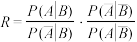 ;
;(ⅱ)利用该调查数据,给出
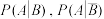 的估计值,并利用(ⅰ)的结果给出R的估计值.
的估计值,并利用(ⅰ)的结果给出R的估计值.附
 ,
,
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |