1 . (1)计算: .
.
(2)解不等式组: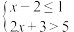
 .
.(2)解不等式组:
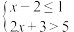
您最近一年使用:0次
名校
2 . 成书于约两千多年前的我国古代数学典籍《九章算术》中记载了通过加减消元求解 元一次方程组的算法,直到拥有超强算力计算机的今天,这仍然是一种效率极高的算法.按照这种算法,求解
元一次方程组的算法,直到拥有超强算力计算机的今天,这仍然是一种效率极高的算法.按照这种算法,求解 元一次方程组大约需要对实系数进行
元一次方程组大约需要对实系数进行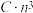 (
( 为给定常数)次计算.1949年,经济学家莱昂提夫为研究“投入产出模型”(该工作后来获得1973年诺贝尔经济学奖),利用当时的计算机求解一个42元一次方程组,花了约56机时.事实上,他的原始模型包含500个未知数,受限于机器算力而不得不进行化简以减少未知数.如果不进行化简,根据未知数个数估计所需机时,结果最接近于( )
为给定常数)次计算.1949年,经济学家莱昂提夫为研究“投入产出模型”(该工作后来获得1973年诺贝尔经济学奖),利用当时的计算机求解一个42元一次方程组,花了约56机时.事实上,他的原始模型包含500个未知数,受限于机器算力而不得不进行化简以减少未知数.如果不进行化简,根据未知数个数估计所需机时,结果最接近于( )
 元一次方程组的算法,直到拥有超强算力计算机的今天,这仍然是一种效率极高的算法.按照这种算法,求解
元一次方程组的算法,直到拥有超强算力计算机的今天,这仍然是一种效率极高的算法.按照这种算法,求解 元一次方程组大约需要对实系数进行
元一次方程组大约需要对实系数进行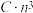 (
( 为给定常数)次计算.1949年,经济学家莱昂提夫为研究“投入产出模型”(该工作后来获得1973年诺贝尔经济学奖),利用当时的计算机求解一个42元一次方程组,花了约56机时.事实上,他的原始模型包含500个未知数,受限于机器算力而不得不进行化简以减少未知数.如果不进行化简,根据未知数个数估计所需机时,结果最接近于( )
为给定常数)次计算.1949年,经济学家莱昂提夫为研究“投入产出模型”(该工作后来获得1973年诺贝尔经济学奖),利用当时的计算机求解一个42元一次方程组,花了约56机时.事实上,他的原始模型包含500个未知数,受限于机器算力而不得不进行化简以减少未知数.如果不进行化简,根据未知数个数估计所需机时,结果最接近于( )A. 机时 机时 | B.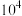 机时 机时 | C.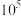 机时 机时 | D.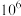 机时 机时 |
您最近一年使用:0次
2022-12-05更新
|
304次组卷
|
3卷引用:北京市海淀区北大附中2023届高三预科部上学期12月阶段练习数学试题
名校
3 . (1)计算: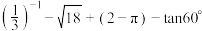 ;
;
(2)先化简,后求值: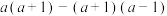 ,其中
,其中 .
.
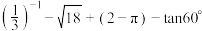 ;
;(2)先化简,后求值:
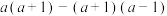 ,其中
,其中 .
.
您最近一年使用:0次
4 . 设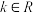 ,对关于
,对关于 的方程组
的方程组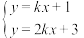 的解的说法正确的是( )
的解的说法正确的是( )
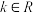 ,对关于
,对关于 的方程组
的方程组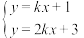 的解的说法正确的是( )
的解的说法正确的是( )A.对任意实数 ,该方程组的解集都是单元素集; ,该方程组的解集都是单元素集; |
B.至少存在一个实数 ,使得该方程组的解集为空集; ,使得该方程组的解集为空集; |
C.至少存在一个实数 ,使得该方程组的解集为无限集; ,使得该方程组的解集为无限集; |
D.对任意实数 ,该方程组的解集都不是空集. ,该方程组的解集都不是空集. |
您最近一年使用:0次
2021-09-24更新
|
812次组卷
|
5卷引用:专题09 集合的概念-2022年暑假初三升高一数学衔接知识自学讲义(人教A版2019)
(已下线)专题09 集合的概念-2022年暑假初三升高一数学衔接知识自学讲义(人教A版2019)第1章 集合 单元综合检测(难点)(已下线)1.1 集合的运算(第4课时)上海市徐汇区位育中学2021-2022学年高一上学期10月月考数学试题(已下线)专题01 集合与常用逻辑用语常考基础题型-2021-2022学年高一《新题速递·数学》(人教A版2019)
5 . 观察实际情景,提出并分析问题
(1)实际情境
企业的生产经营活动,最终以利润论成败,利润的本质是企业盈利的表现形式,是全体职工的劳动成绩,企业为市场生产优质商品而得到利润,注意利润是对全部成本而言的.一个企业有利润,意味着该企业有一定的盈利能力,意味着企业具有较强的获取现金的能力,影响利润的因素较复杂,如果排除一些较为复杂的因素,我们是否可以预测利润,为企业的发展献计献策?
(2)提出问题
为长期获得可观的利润,应该如何制定企业的发展策略?
(3)分析问题
某新型企业为获得更大利润,须不断加大投资,企业的发展必然受到利润率的制约,若预计年利润低于10%时,则该企业就考虑转型,我们可以根据企业成本与利润的数据,通过数学模型达到转型预测的目的.
2. 收集数据
下表显示的是某企业几年来利润y(百万元)与年投资成本x(百万元)变化的一组数据:
①选择一个恰当的函数模型来描述x,y之间的关系,并求出其解析式;
②试判断该企业年利润不低于6百万元时,该企业是否要考虑转型.
3.分析数据
先根据表中数据,刻画出散点图,根据散点图的特征选择合适的函数.利用几何画板等工具,得到的散点图如下图:
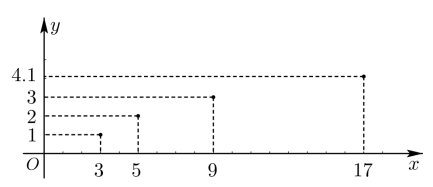
根据散点图的形式,结合我们所学的函数图像,发现模型的不确定.
4.建立模型
(1)幂函数型
根据散点图的形式,可假设 (
( ,且
,且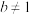 ),
),
则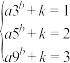 ,化简得到
,化简得到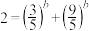 ,
,
设,利用几何画板、图形计算器等可求得此方程的解为 ,不合题意舍.
,不合题意舍.
(2)对数函数模型
设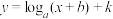 (
( ,且
,且 ),
),
则 ,解得
,解得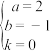 ,∴
,∴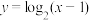 .
.
(3)指数函数模型
设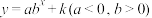 ,
,
则 ,故
,故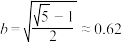 ,
,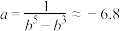 ,
,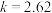 ,
,
故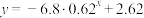 ,
,
但当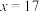 时,
时,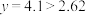 ,故指数函数模型不合适.
,故指数函数模型不合适.
结合以上分析,我们发现对数函数函数模型较为合适.
5.检验模型
我们用余下的数据进行检验,
当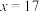 时,
时, ;当
;当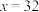 ,
, ,这两组数据与实际的数据比较接近,故选择对数函数模型.
,这两组数据与实际的数据比较接近,故选择对数函数模型.
6.问题解决
由题知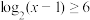 ,解得
,解得 .,
.,
∵年利润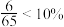 ,∴该企业要考虑转型.
,∴该企业要考虑转型.
7.问题拓展
在上述模型的建立的过程中,我们根据散点图选择了不同的函数模型,然后利用前3个点求出对应的函数形式,否定了其中两个不合的函数模型,那么请同学思考一下是否有更合适的模型?
(1)实际情境
企业的生产经营活动,最终以利润论成败,利润的本质是企业盈利的表现形式,是全体职工的劳动成绩,企业为市场生产优质商品而得到利润,注意利润是对全部成本而言的.一个企业有利润,意味着该企业有一定的盈利能力,意味着企业具有较强的获取现金的能力,影响利润的因素较复杂,如果排除一些较为复杂的因素,我们是否可以预测利润,为企业的发展献计献策?
(2)提出问题
为长期获得可观的利润,应该如何制定企业的发展策略?
(3)分析问题
某新型企业为获得更大利润,须不断加大投资,企业的发展必然受到利润率的制约,若预计年利润低于10%时,则该企业就考虑转型,我们可以根据企业成本与利润的数据,通过数学模型达到转型预测的目的.
2. 收集数据
下表显示的是某企业几年来利润y(百万元)与年投资成本x(百万元)变化的一组数据:
| 年份 | 2015 | 2016 | 2017 | 2018 | 2019 | |||
投资成本 | 3 | 5 | 9 | 17 | 33 | … | ||
年利润 | 1 | 2 | 3 | 4.1 | 5.2 | … | ||
②试判断该企业年利润不低于6百万元时,该企业是否要考虑转型.
3.分析数据
先根据表中数据,刻画出散点图,根据散点图的特征选择合适的函数.利用几何画板等工具,得到的散点图如下图:

根据散点图的形式,结合我们所学的函数图像,发现模型的不确定.
4.建立模型
(1)幂函数型
根据散点图的形式,可假设
 (
( ,且
,且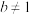 ),
),则
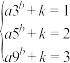 ,化简得到
,化简得到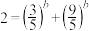 ,
,设,利用几何画板、图形计算器等可求得此方程的解为
 ,不合题意舍.
,不合题意舍.
(2)对数函数模型
设
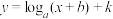 (
( ,且
,且 ),
),则
 ,解得
,解得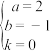 ,∴
,∴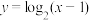 .
.(3)指数函数模型
设
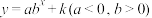 ,
,则
 ,故
,故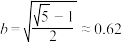 ,
,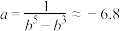 ,
,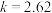 ,
,故
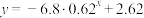 ,
,但当
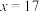 时,
时,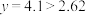 ,故指数函数模型不合适.
,故指数函数模型不合适.结合以上分析,我们发现对数函数函数模型较为合适.
5.检验模型
我们用余下的数据进行检验,
当
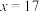 时,
时, ;当
;当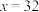 ,
, ,这两组数据与实际的数据比较接近,故选择对数函数模型.
,这两组数据与实际的数据比较接近,故选择对数函数模型.6.问题解决
由题知
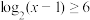 ,解得
,解得 .,
.,∵年利润
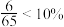 ,∴该企业要考虑转型.
,∴该企业要考虑转型.7.问题拓展
在上述模型的建立的过程中,我们根据散点图选择了不同的函数模型,然后利用前3个点求出对应的函数形式,否定了其中两个不合的函数模型,那么请同学思考一下是否有更合适的模型?
您最近一年使用:0次
名校
6 . 已知函数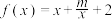 (
( 为常数)
为常数)
(1)定义:区间 的长度为
的长度为 ,若
,若 ,问是否存在区间
,问是否存在区间 ,使得
,使得 时,
时, 的值域为
的值域为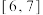 ,若存在,求出此区间长度的最大值;
,若存在,求出此区间长度的最大值;
(2)解关于 的不等式:
的不等式: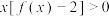 ;
;
(3)求函数 在
在 上的最小值.
上的最小值.
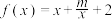 (
( 为常数)
为常数)(1)定义:区间
 的长度为
的长度为 ,若
,若 ,问是否存在区间
,问是否存在区间 ,使得
,使得 时,
时, 的值域为
的值域为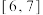 ,若存在,求出此区间长度的最大值;
,若存在,求出此区间长度的最大值;(2)解关于
 的不等式:
的不等式: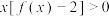 ;
;(3)求函数
 在
在 上的最小值.
上的最小值.
您最近一年使用:0次
名校
解题方法
7 . 记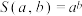 ,其中
,其中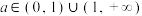 ,例如
,例如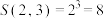 .
.
(1)若 ,求
,求 的取值集合;
的取值集合;
(2)解关于 的不等式
的不等式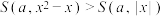 ;
;
(3)已知对任意正整数 ,实数
,实数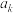 满足
满足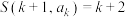 ,记
,记 ,其中n为正整数,若
,其中n为正整数,若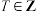 且
且 ,求
,求 的取值集合.
的取值集合.
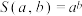 ,其中
,其中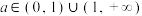 ,例如
,例如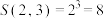 .
.(1)若
 ,求
,求 的取值集合;
的取值集合;(2)解关于
 的不等式
的不等式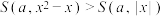 ;
;(3)已知对任意正整数
 ,实数
,实数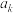 满足
满足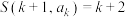 ,记
,记 ,其中n为正整数,若
,其中n为正整数,若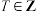 且
且 ,求
,求 的取值集合.
的取值集合.
您最近一年使用:0次
2022-09-06更新
|
457次组卷
|
4卷引用:期中模拟预测卷02(测试范围:前三章)-2022-2023学年高一数学上学期期中期末考点大串讲(沪教版2020必修第一册)
(已下线)期中模拟预测卷02(测试范围:前三章)-2022-2023学年高一数学上学期期中期末考点大串讲(沪教版2020必修第一册)上海市建平中学2021-2022学年高一上学期期中数学试题内蒙古自治区赤峰市红山区2022-2023学年高一上学期期末数学试题(已下线)第二章 等式与不等式(压轴必刷30题7种题型专项训练)-【满分全攻略】(沪教版2020必修第一册)
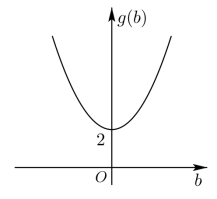
8 . 在下列两个条件中任选一个补充在下面的问题中,并回答问题.
①b为自变量x,c为关于b(即x)的函数,记为y;
②c为自变量x,b为关于c(即x)的函数,记为y.
问题:对于等式ab=c(a>0,a≠1),若视a为常数,______,且函数y=f(x)的图象经过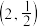 .
.
(1)求 的解析式,并写出
的解析式,并写出 的单调区间;
的单调区间;
(2)解关于x的不等式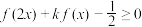 .
.
①b为自变量x,c为关于b(即x)的函数,记为y;
②c为自变量x,b为关于c(即x)的函数,记为y.
问题:对于等式ab=c(a>0,a≠1),若视a为常数,______,且函数y=f(x)的图象经过
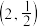 .
.(1)求
 的解析式,并写出
的解析式,并写出 的单调区间;
的单调区间;(2)解关于x的不等式
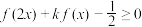 .
.
您最近一年使用:0次
2022-03-01更新
|
374次组卷
|
3卷引用:江苏省南通市2021-2022学年高一上学期期末数学试题
解题方法
9 . 研究函数首先要研究其性质和图象,然后利用性质和图象来解决问题如探究函数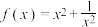 .
.
(1)探究性质
①求 的定义域并判断
的定义域并判断 奇偶性;
奇偶性;
②讨论 的单调性;
的单调性;
(2)解关于x的不等式: .
.
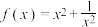 .
.(1)探究性质
①求
 的定义域并判断
的定义域并判断 奇偶性;
奇偶性;②讨论
 的单调性;
的单调性;(2)解关于x的不等式:
 .
.
您最近一年使用:0次
解题方法
10 . 幂函数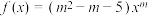 是偶函数,
是偶函数,
(1)求 的值,写出
的值,写出 解析式;
解析式;
(2)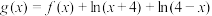 ,
,
①判断 的奇偶性,并用定义证明;
的奇偶性,并用定义证明;
②指出 的单调递减区间(无需证明),并解关于实数
的单调递减区间(无需证明),并解关于实数 的不等式
的不等式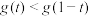 .
.
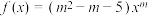 是偶函数,
是偶函数,(1)求
 的值,写出
的值,写出 解析式;
解析式;(2)
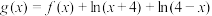 ,
,①判断
 的奇偶性,并用定义证明;
的奇偶性,并用定义证明;②指出
 的单调递减区间(无需证明),并解关于实数
的单调递减区间(无需证明),并解关于实数 的不等式
的不等式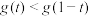 .
.
您最近一年使用:0次



