解题方法
1 . 如图,在三棱锥 中,
中,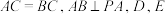 分别是
分别是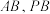 的中点.
的中点. 平面
平面 ;
;
(2)求证: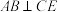 .
.
请先写出第(1)问的解答过程,然后阅读下面第(2)问的解答过程.
在第(2)问的解答过程中,设置了①~③三个空格,如下的表格中为每个空格给出了两个选项,其中只有一个符合逻辑推理.请选出符合逻辑推理的选项,并填写在横线上(只需填写“A”或“B”).
 中,
中,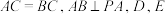 分别是
分别是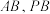 的中点.
的中点.
 平面
平面 ;
;(2)求证:
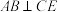 .
.请先写出第(1)问的解答过程,然后阅读下面第(2)问的解答过程.
证明:(2)因为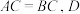 是 是 的中点, 的中点,所以①_________. 因为  ,由(1)知, ,由(1)知, , ,所以②_________ 所以③_________. 所以 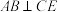 . . |
| 空格序号 | 选项 | |
| ① | (A) | (B) |
| ② | (A)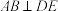 | (B) 平面 平面 |
| ③ | (A) 平面 平面 | (B) 平面 平面 |
您最近一年使用:0次
名校
解题方法
2 . 如图,在四棱锥 中,底面
中,底面 是菱形,
是菱形, 平面
平面 ,E为
,E为 的中点.
的中点. 平面
平面 ;
;
(2)求证: 平面
平面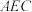 .
.
 中,底面
中,底面 是菱形,
是菱形, 平面
平面 ,E为
,E为 的中点.
的中点.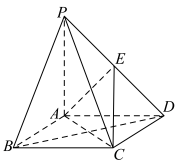
 平面
平面 ;
;(2)求证:
 平面
平面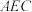 .
.
您最近一年使用:0次
2024-01-17更新
|
2329次组卷
|
9卷引用:北京市第一次普通高中2023-2024学年高二上学期学业水平合格性考试数学试题
北京市第一次普通高中2023-2024学年高二上学期学业水平合格性考试数学试题(已下线)第12讲 8.6.2直线与平面垂直的判定定理(第1课时)-【帮课堂】(人教A版2019必修第二册)(已下线)第17讲 第八章 立体几何初步 章末重点题型大总结-【帮课堂】(人教A版2019必修第二册)(已下线)13.2.3 直线与平面的位置关系(2)-【帮课堂】(苏教版2019必修第二册)(已下线)11.4.1直线与平面垂直-同步精品课堂(人教B版2019必修第四册)(已下线)专题06 立体几何初步解答题热点题型-《期末真题分类汇编》(江苏专用)广西南宁市第三中学2023-2024学年高一下学期月考(三)数学试题江苏省苏州市相城区陆慕高级中学2023-2024学年高一下学期5月月考数学试题福建省泉州市安溪第八中学2023-2024学年高一下学期6月份质量检测数学试题
解题方法
3 . 如图,在四棱锥 中,
中, 平面
平面 ,底面
,底面 是矩形.
是矩形. 平面
平面 ;
;
(2)求证: 平面
平面 .
.
 中,
中, 平面
平面 ,底面
,底面 是矩形.
是矩形.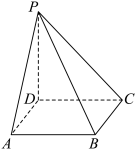
 平面
平面 ;
;(2)求证:
 平面
平面 .
.
您最近一年使用:0次
解题方法
4 . 阅读下面题目及其解答过程.
以上题目的解答过程中,设置了①~⑤五个空格,如下的表格中为每个空格给出了两个选项,其中只有一个符合推理,请选出符合推理的选项,并填写在答题卡的指定位置(只需填写“A”或“B”).
如图,已知正方体 . .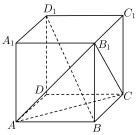 (Ⅰ)求证:  ; ;(Ⅱ)求证:直线 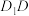 与平面 与平面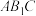 不平行. 不平行.解:(Ⅰ)如图,连接 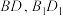 . .因为  为正方体, 为正方体,所以  平面 平面 . .所以①___________. 因为四边形  为正方形, 为正方形,所以②__________. 因为 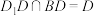 , ,所以③____________. 所以  . .(Ⅱ)如图,设 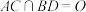 ,连接 ,连接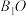 . .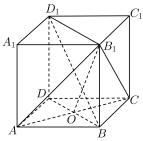 假设 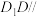 平面 平面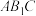 . .因为 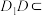 平面 平面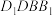 ,且平面 ,且平面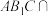 平面 平面 ④____________, ④____________,所以⑤__________. 又 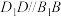 , ,这样过点  有两条直线 有两条直线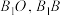 都与 都与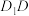 平行,显然不可能. 平行,显然不可能.所以直线 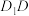 与平面 与平面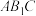 不平行. 不平行. |
| 空格序号 | 选项 |
| ① | A.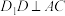 B. B.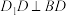 |
| ② | A. B. B.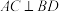 |
| ③ | A.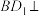 平面 平面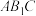 B. B. 平面 平面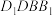 |
| ④ | A.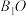 B. B. |
| ⑤ | A.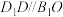 B. B.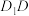 与 与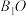 为相交直线 为相交直线 |
您最近一年使用:0次
2022-03-11更新
|
744次组卷
|
2卷引用:北京市第一次普通高中2022届高三学业水平合格性考试数学试题
名校
解题方法
5 . 如图,在四棱锥 中,底面
中,底面 是正方形,
是正方形, 平面
平面 .
.

(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面 .
.
 中,底面
中,底面 是正方形,
是正方形, 平面
平面 .
.
(1)求证:
 平面
平面 ;
;(2)求证:
 平面
平面 .
.
您最近一年使用:0次
2022-01-13更新
|
1490次组卷
|
3卷引用:北京市普通高中2021-2022学年高二第二次学业水平合格性考试数学试题
名校
解题方法
6 . 如图,在三棱锥O-ABC中,OA,OB,OC两两互相垂直,OA=OB,且D,E,F分别为AC,BC,AB的中点.
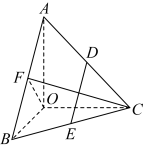
(1)求证: 平面AOB;
平面AOB;
(2)求证:AB⊥平面OCF.

(1)求证:
 平面AOB;
平面AOB;(2)求证:AB⊥平面OCF.
您最近一年使用:0次
2021-07-05更新
|
1108次组卷
|
3卷引用:北京市2020-2021学年高二第一次普通高中学业水平合格性考试数学试题
7 . 已知直线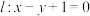 与圆
与圆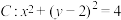 交于两点
交于两点 ,求
,求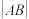 .
.
某同学的解答过程如下:
指出上述解答过程中的错误之处,并写出正确的解答过程.
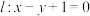 与圆
与圆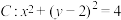 交于两点
交于两点 ,求
,求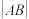 .
.某同学的解答过程如下:
解答:设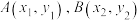 . .联立方程组  消去  ,整理得 ,整理得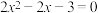 . .此方程根的判别式 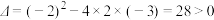 . .所以  . .所以 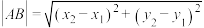 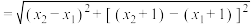 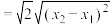 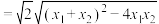 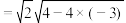  . .所以  . . |
您最近一年使用:0次
8 . 已知圆 的圆心坐标为
的圆心坐标为 ,且与
,且与 轴相切,直线
轴相切,直线 与圆
与圆 交于
交于 ,
, 两点,求
两点,求 .
.
某同学的解答过程如下:
解答:因为圆 的圆心坐标为
的圆心坐标为 ,且与
,且与 轴相切,
轴相切,
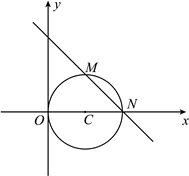
所以圆 的半径是2.
的半径是2.
所以圆 的方程是
的方程是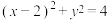 .
.
因为直线 与圆
与圆 交于
交于 ,
, 两点,
两点,
联立方程组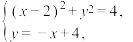
解得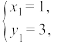 或
或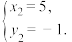
不妨设 ,
,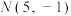 ,
,
所以
(1)指出上述解答过程中的错误之处;
(2)写出正确的解答过程.
 的圆心坐标为
的圆心坐标为 ,且与
,且与 轴相切,直线
轴相切,直线 与圆
与圆 交于
交于 ,
, 两点,求
两点,求 .
.某同学的解答过程如下:
解答:因为圆
 的圆心坐标为
的圆心坐标为 ,且与
,且与 轴相切,
轴相切,
所以圆
 的半径是2.
的半径是2.所以圆
 的方程是
的方程是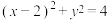 .
.因为直线
 与圆
与圆 交于
交于 ,
, 两点,
两点,联立方程组
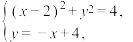
解得
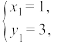 或
或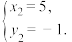
不妨设
 ,
,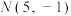 ,
,所以

(1)指出上述解答过程中的错误之处;
(2)写出正确的解答过程.
您最近一年使用:0次
9 . 某同学解答一道解析几何题:“已知直线l: 与x轴的交点为A,圆O:
与x轴的交点为A,圆O: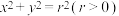 经过点A.
经过点A.
(Ⅰ)求r的值;
(Ⅱ)若点B为圆O上一点,且直线AB垂直于直线l,求 .”
.”
该同学解答过程如下:
解答:(Ⅰ)令 ,即
,即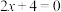 ,解得
,解得 ,所以点A的坐标为
,所以点A的坐标为 .
.
因为圆O: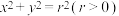 经过点A,所以
经过点A,所以 .
.
(Ⅱ)因为 .所以直线AB的斜率为
.所以直线AB的斜率为 .
.
所以直线AB的方程为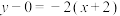 ,即
,即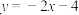 .
.
代入 消去y整理得
消去y整理得 ,
,
解得 ,
,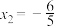 .当
.当 时,
时, .所以点B的坐标为
.所以点B的坐标为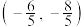 .
.
所以 .
.
指出上述解答过程中的错误之处,并写出正确的解答过程.
 与x轴的交点为A,圆O:
与x轴的交点为A,圆O: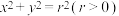 经过点A.
经过点A.(Ⅰ)求r的值;
(Ⅱ)若点B为圆O上一点,且直线AB垂直于直线l,求
 .”
.”该同学解答过程如下:
解答:(Ⅰ)令
 ,即
,即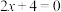 ,解得
,解得 ,所以点A的坐标为
,所以点A的坐标为 .
.因为圆O:
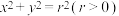 经过点A,所以
经过点A,所以 .
.(Ⅱ)因为
 .所以直线AB的斜率为
.所以直线AB的斜率为 .
.所以直线AB的方程为
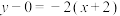 ,即
,即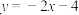 .
.代入
 消去y整理得
消去y整理得 ,
,解得
 ,
, .当
.当 时,
时, .所以点B的坐标为
.所以点B的坐标为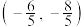 .
.所以
 .
.指出上述解答过程中的错误之处,并写出正确的解答过程.
您最近一年使用:0次
2019-10-22更新
|
520次组卷
|
2卷引用:2019年北京市第二次普通高中学业水平合格性考试数学试题
10 . 如图,在三棱锥 中,
中, 平面ABC,点D,E,F分别为PC,AB,AC的中点.
平面ABC,点D,E,F分别为PC,AB,AC的中点.
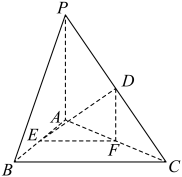
(Ⅰ)求证: 平面DEF;
平面DEF;
(Ⅱ)求证: .
.
阅读下面给出的解答过程及思路分析.
解答:(Ⅰ)证明:在 中,因为E,F分别为AB,AC的中点,所以①.
中,因为E,F分别为AB,AC的中点,所以①.
因为 平面DEF,
平面DEF,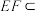 平面DEF,所以
平面DEF,所以 平面DEF.
平面DEF.
(Ⅱ)证明:因为 平面ABC,
平面ABC, 平面ABC,所以②.
平面ABC,所以②.
因为D,F分别为PC,AC的中点,所以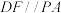 .所以
.所以 .
.
思路分析:第(Ⅰ)问是先证③,再证“线面平行”;
第(Ⅱ)问是先证④,再证⑤,最后证“线线垂直”.
以上证明过程及思路分析中,设置了①~⑤五个空格,如下的表格中为每个空格给出了三个选项,其中只有一个正确,请选出你认为正确的选项,并填写在答题卡的指定位置.
 中,
中, 平面ABC,点D,E,F分别为PC,AB,AC的中点.
平面ABC,点D,E,F分别为PC,AB,AC的中点.
(Ⅰ)求证:
 平面DEF;
平面DEF;(Ⅱ)求证:
 .
.阅读下面给出的解答过程及思路分析.
解答:(Ⅰ)证明:在
 中,因为E,F分别为AB,AC的中点,所以①.
中,因为E,F分别为AB,AC的中点,所以①.因为
 平面DEF,
平面DEF,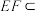 平面DEF,所以
平面DEF,所以 平面DEF.
平面DEF.(Ⅱ)证明:因为
 平面ABC,
平面ABC, 平面ABC,所以②.
平面ABC,所以②.因为D,F分别为PC,AC的中点,所以
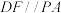 .所以
.所以 .
.思路分析:第(Ⅰ)问是先证③,再证“线面平行”;
第(Ⅱ)问是先证④,再证⑤,最后证“线线垂直”.
以上证明过程及思路分析中,设置了①~⑤五个空格,如下的表格中为每个空格给出了三个选项,其中只有一个正确,请选出你认为正确的选项,并填写在答题卡的指定位置.
| 空格 | 选项 | ||
| ① | A.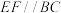 | B.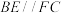 | C.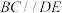 |
| ② | A.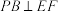 | B.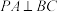 | C. |
| ③ | A.线线垂直 | B.线面垂直 | C.线线平行 |
| ④ | A.线线垂直 | B.线面垂直 | C.线线平行 |
| ⑤ | A.线面平行 | B.线线平行 | C.线面垂直 |
您最近一年使用:0次



