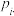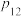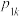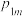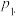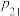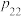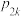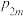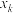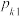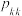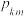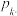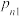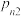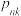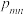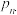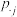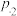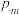名校
解题方法
1 . 基本不等式可以推广到一般的情形:对于 个正数
个正数 ,它们的算术平均不小于它们的几何平均,即
,它们的算术平均不小于它们的几何平均,即 ,当且仅当
,当且仅当 时,等号成立.若无穷正项数列
时,等号成立.若无穷正项数列 同时满足下列两个性质:①
同时满足下列两个性质:①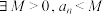 ;②
;② 为单调数列,则称数列
为单调数列,则称数列 具有性质
具有性质 .
.
(1)若 ,求数列
,求数列 的最小项;
的最小项;
(2)若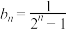 ,记
,记 ,判断数列
,判断数列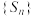 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;
(3)若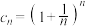 ,求证:数列
,求证:数列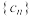 具有性质
具有性质 .
.
 个正数
个正数 ,它们的算术平均不小于它们的几何平均,即
,它们的算术平均不小于它们的几何平均,即 ,当且仅当
,当且仅当 时,等号成立.若无穷正项数列
时,等号成立.若无穷正项数列 同时满足下列两个性质:①
同时满足下列两个性质:①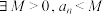 ;②
;② 为单调数列,则称数列
为单调数列,则称数列 具有性质
具有性质 .
.(1)若
 ,求数列
,求数列 的最小项;
的最小项;(2)若
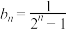 ,记
,记 ,判断数列
,判断数列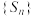 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;(3)若
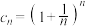 ,求证:数列
,求证:数列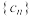 具有性质
具有性质 .
.
您最近一年使用:0次
2024-02-21更新
|
3108次组卷
|
6卷引用:湖北省荆州市沙市中学2024届高三下学期3月月考数学试题
湖北省荆州市沙市中学2024届高三下学期3月月考数学试题安徽省部分省示范高中2024届高三开学联考数学试卷湖南省2024年高三数学新改革提高训练三(九省联考题型)(已下线)黄金卷04(2024新题型)广东省广州市西关外国语学校2023-2024学年高二下学期期中数学试题(已下线)压轴题03不等式压轴题13题型汇总-2
名校
2 . 设 的所有可能取值为
的所有可能取值为 ,称
,称 (
(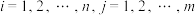 )为二维离散随机变量
)为二维离散随机变量 的联合分布列,用表格表示为:
的联合分布列,用表格表示为:
仿照条件概率的定义,有如下离散随机变量的条件分布列:定义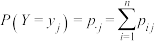 ,对于固定的
,对于固定的 ,若
,若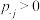 ,则称
,则称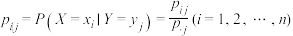 为给定
为给定 条件下的
条件下的 条件分布列.
条件分布列.
离散随机变量的条件分布的数学期望(若存在)定义如下: .
.
(1)设二维离散随机变量 的联合分布列为
的联合分布列为
求给定 条件下的
条件下的 条件分布列;
条件分布列;
(2)设 为二维离散随机变量,且
为二维离散随机变量,且 存在,证明:
存在,证明: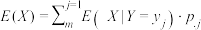 ;
;
(3)某人被困在有三个门的迷宫里,第一个门通向离开迷宫的道,沿此道走30分钟可走出迷宫;第二个门通一条迷道,沿此迷道走50分钟又回到原处;第三个门通一条迷道,沿此迷道走70分钟也回到原处.假定此人总是等可能地在三个门中选择一个,试求他平均要用多少时间才能走出迷宫.
 的所有可能取值为
的所有可能取值为 ,称
,称 (
(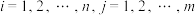 )为二维离散随机变量
)为二维离散随机变量 的联合分布列,用表格表示为:
的联合分布列,用表格表示为:Y X |
|
| … |
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
| … |
|
|
… | … | … | … | … | … | … | … |
|
|
| … |
| … |
|
|
… | … | … | … | … | … | … | … |
|
|
| … |
| … |
|
|
|
|
| … |
| … |
| 1 |
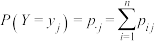 ,对于固定的
,对于固定的 ,若
,若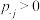 ,则称
,则称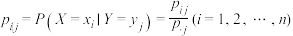 为给定
为给定 条件下的
条件下的 条件分布列.
条件分布列.离散随机变量的条件分布的数学期望(若存在)定义如下:
 .
.(1)设二维离散随机变量
 的联合分布列为
的联合分布列为Y X | 1 | 2 | 3 |
|
1 | 0.1 | 0.3 | 0.2 | 0.6 |
2 | 0.05 | 0.2 | 0.15 | 0.4 |
| 0.15 | 0.5 | 0.35 | 1 |
 条件下的
条件下的 条件分布列;
条件分布列;(2)设
 为二维离散随机变量,且
为二维离散随机变量,且 存在,证明:
存在,证明: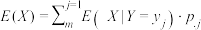 ;
;(3)某人被困在有三个门的迷宫里,第一个门通向离开迷宫的道,沿此道走30分钟可走出迷宫;第二个门通一条迷道,沿此迷道走50分钟又回到原处;第三个门通一条迷道,沿此迷道走70分钟也回到原处.假定此人总是等可能地在三个门中选择一个,试求他平均要用多少时间才能走出迷宫.
您最近一年使用:0次
2024-03-29更新
|
738次组卷
|
3卷引用:湖北省(圆创)高中名校联盟2024届高三下学期3月月考数学试题
名校
3 . 人口老龄化加剧的背景下,我国先后颁布了一系列生育政策,根据不同政策要求,分为两个时期Ⅰ和Ⅱ.根据部分调查数据总结出如下规律:对于同一个家庭,在Ⅰ时期内生孩 人,在Ⅱ时期生孩
人,在Ⅱ时期生孩 人,(不考虑多胞胎)生男生女的概率相等.
人,(不考虑多胞胎)生男生女的概率相等. 服从0-1分布且
服从0-1分布且 .
. 分布列如下图:
分布列如下图:
现已知一个家庭在Ⅰ时期没生孩子,则在Ⅱ时期生2个孩子概率为 ;若在Ⅰ时期生了1个女孩,则在时期生2个孩子概率为
;若在Ⅰ时期生了1个女孩,则在时期生2个孩子概率为 ;若在Ⅰ时期生了1个男孩,则在Ⅱ时期生2个孩子概率为
;若在Ⅰ时期生了1个男孩,则在Ⅱ时期生2个孩子概率为 ,样本点中Ⅰ时期生孩人数与Ⅱ时期生孩人数之比为
,样本点中Ⅰ时期生孩人数与Ⅱ时期生孩人数之比为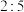 (针对普遍家庭).
(针对普遍家庭).
(1)求 的期望与方差;
的期望与方差;
(2)由数据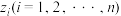 组成的样本空间根据分层随机抽样分为两层,样本点之比为
组成的样本空间根据分层随机抽样分为两层,样本点之比为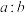 ,分别为
,分别为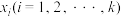 与
与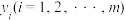 ,
,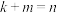 ,总体样本点与两个分层样本点均值分别为
,总体样本点与两个分层样本点均值分别为 ,
, ,
,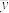 ,方差分别为
,方差分别为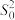 ,
,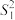 ,
,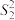 ,证明:
,证明: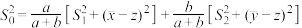 ,并利用该公式估算题设样本总体的方差.
,并利用该公式估算题设样本总体的方差.
 人,在Ⅱ时期生孩
人,在Ⅱ时期生孩 人,(不考虑多胞胎)生男生女的概率相等.
人,(不考虑多胞胎)生男生女的概率相等. 服从0-1分布且
服从0-1分布且 .
. 分布列如下图:
分布列如下图: | 0 | 1 | 2 |
 |  |  |  |
 ;若在Ⅰ时期生了1个女孩,则在时期生2个孩子概率为
;若在Ⅰ时期生了1个女孩,则在时期生2个孩子概率为 ;若在Ⅰ时期生了1个男孩,则在Ⅱ时期生2个孩子概率为
;若在Ⅰ时期生了1个男孩,则在Ⅱ时期生2个孩子概率为 ,样本点中Ⅰ时期生孩人数与Ⅱ时期生孩人数之比为
,样本点中Ⅰ时期生孩人数与Ⅱ时期生孩人数之比为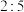 (针对普遍家庭).
(针对普遍家庭).(1)求
 的期望与方差;
的期望与方差;(2)由数据
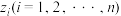 组成的样本空间根据分层随机抽样分为两层,样本点之比为
组成的样本空间根据分层随机抽样分为两层,样本点之比为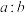 ,分别为
,分别为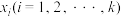 与
与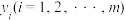 ,
,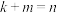 ,总体样本点与两个分层样本点均值分别为
,总体样本点与两个分层样本点均值分别为 ,
, ,
,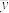 ,方差分别为
,方差分别为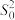 ,
,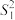 ,
,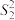 ,证明:
,证明: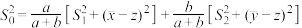 ,并利用该公式估算题设样本总体的方差.
,并利用该公式估算题设样本总体的方差.
您最近一年使用:0次
2023-08-02更新
|
1158次组卷
|
8卷引用:湖北省武昌实验中学2023-2024学年高三上学期10月月考数学试题
湖北省武昌实验中学2023-2024学年高三上学期10月月考数学试题浙江省名校联盟2022-2023学年高二下学期期末联考数学试题广东省深圳市宝安区2024届高三上学期10月调研数学试题(已下线)第二节 用样本的数字特征估计总体 B卷素养养成卷 一轮复习点点通(已下线)专题03 条件概率与全概率公式(4)(已下线)高二下学期期末数学试卷(巩固篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)重庆市第一中学校2023-2024学年高二下学期5月月考数学试题(已下线)专题02概率统计期末10种常考题型归类【好题汇编】-备战2023-2024学年高二数学下学期期末真题分类汇编(人教B版2019选择性必修第二册)
名校
4 . 甲、乙两人进行象棋比赛,赛前每人发3枚筹码.一局后负的一方,需将自己的一枚筹码给对方;若平局,双方的筹码不动,当一方无筹码时,比赛结束,另一方最终获胜.由以往两人的比赛结果可知,在一局中甲胜的概率为0.3、乙胜的概率为0.2.
(1)第一局比赛后,甲的筹码个数记为 ,求
,求 的分布列和期望;
的分布列和期望;
(2)求四局比赛后,比赛结束的概率;
(3)若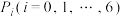 表示“在甲所得筹码为
表示“在甲所得筹码为 枚时,最终甲获胜的概率”,则
枚时,最终甲获胜的概率”,则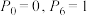 .证明:
.证明: 为等比数列.
为等比数列.
(1)第一局比赛后,甲的筹码个数记为
 ,求
,求 的分布列和期望;
的分布列和期望;(2)求四局比赛后,比赛结束的概率;
(3)若
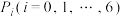 表示“在甲所得筹码为
表示“在甲所得筹码为 枚时,最终甲获胜的概率”,则
枚时,最终甲获胜的概率”,则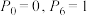 .证明:
.证明: 为等比数列.
为等比数列.
您最近一年使用:0次
2023-07-20更新
|
1812次组卷
|
6卷引用:湖北省武汉市第四十九中学2024届高三上学期九月调考模拟数学试题(二)
湖北省武汉市第四十九中学2024届高三上学期九月调考模拟数学试题(二)河北省张家口市2023届高三三模数学试题山西省运城市运城中学2023届高三第二次模拟数学试题福建省福州市四校2022-2023学年高二下学期期末联考数学试题(已下线)微考点7-2 递推方法计算概率与一维马尔科夫过程(数列与概率结合)(已下线)2024届高三开学摸底考试
名校
解题方法
5 . 一个袋子中装有大小和质地相同的4个球,其中有2个红球(标号为1和2),2个白球(标号为3和4),甲、乙两人先后从袋中不放回地各摸出1个球.设“甲摸到红球”为事件 ,“乙摸到红球”为事件
,“乙摸到红球”为事件 .
.
(1)小明同学认为:由于甲先摸球,所以事件 发生的可能性大于
发生的可能性大于 发生的可能性.小明的判断是否正确,请说明理由;
发生的可能性.小明的判断是否正确,请说明理由;
(2)判断事件 与
与 是否相互独立,并证明.
是否相互独立,并证明.
 ,“乙摸到红球”为事件
,“乙摸到红球”为事件 .
.(1)小明同学认为:由于甲先摸球,所以事件
 发生的可能性大于
发生的可能性大于 发生的可能性.小明的判断是否正确,请说明理由;
发生的可能性.小明的判断是否正确,请说明理由;(2)判断事件
 与
与 是否相互独立,并证明.
是否相互独立,并证明.
您最近一年使用:0次
2023-06-29更新
|
515次组卷
|
5卷引用:湖北省随州市第一中学2023-2024学年高二上学期8月月考数学试题
2023·全国·模拟预测
名校
6 . 某中学举办了诗词大会选拔赛,共有两轮比赛,第一轮是诗词接龙,第二轮是飞花令.第一轮给每位选手提供5个诗词接龙的题目,选手从中抽取2个题目,主持人说出诗词的上句,若选手在10秒内正确回答出下句可得10分,若不能在10秒内正确回答出下句得0分.
(1)已知某位选手会5个诗词接龙题目中的3个,求该选手在第一轮得分的数学期望;
(2)已知恰有甲、乙、丙、丁四个团队参加飞花令环节的比赛,每一次由四个团队中的一个回答问题,无论答题对错,该团队回答后由其他团队抢答下一问题,且其他团队有相同的机会抢答下一问题.记第n次回答的是甲的概率为 ,若
,若 .
.
①求P2,P3;
②证明:数列 为等比数列,并比较第7次回答的是甲和第8次回答的是甲的可能性的大小.
为等比数列,并比较第7次回答的是甲和第8次回答的是甲的可能性的大小.
(1)已知某位选手会5个诗词接龙题目中的3个,求该选手在第一轮得分的数学期望;
(2)已知恰有甲、乙、丙、丁四个团队参加飞花令环节的比赛,每一次由四个团队中的一个回答问题,无论答题对错,该团队回答后由其他团队抢答下一问题,且其他团队有相同的机会抢答下一问题.记第n次回答的是甲的概率为
 ,若
,若 .
.①求P2,P3;
②证明:数列
 为等比数列,并比较第7次回答的是甲和第8次回答的是甲的可能性的大小.
为等比数列,并比较第7次回答的是甲和第8次回答的是甲的可能性的大小.
您最近一年使用:0次
2023-02-17更新
|
2645次组卷
|
9卷引用:湖北省荆州中学2023-2024学年高三上学期10月半月考数学试题
湖北省荆州中学2023-2024学年高三上学期10月半月考数学试题(已下线)2023年普通高等学校招生全国统一考试数学预测卷(四)(已下线)2023年四省联考变试题17-22(已下线)7.4 二项分布与超几何分布(练习)-2022-2023学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)重难点突破01 数列的综合应用 (十三大题型)-2(已下线)重难点突破01 概率与统计的综合应用(十八大题型)-2广东省惠州市惠东县2024届高三上学期第二次教学质量检测数学试题(已下线)考点19 概率中的数列 2024届高考数学考点总动员(已下线)专题21 概率与统计的综合运用(13大题型)(练习)
7 . 从有3个红球和3个蓝球的袋中,每次随机摸出1个球,摸出的球不再放回,记 表示事件“第
表示事件“第 次摸到红球”,
次摸到红球”, ,2,…,6.
,2,…,6.
(1)求第一次摸到蓝球的条件下第二次摸到红球的概率;
(2)记 表示
表示 ,
, ,
, 同时发生的概率,
同时发生的概率, 表示已知
表示已知 与
与 都发生时
都发生时 发生的概率.
发生的概率.
(ⅰ)证明: ;
;
(ⅱ)求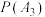 .
.
 表示事件“第
表示事件“第 次摸到红球”,
次摸到红球”, ,2,…,6.
,2,…,6.(1)求第一次摸到蓝球的条件下第二次摸到红球的概率;
(2)记
 表示
表示 ,
, ,
, 同时发生的概率,
同时发生的概率, 表示已知
表示已知 与
与 都发生时
都发生时 发生的概率.
发生的概率.(ⅰ)证明:
 ;
;(ⅱ)求
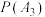 .
.
您最近一年使用:0次
2023-01-12更新
|
945次组卷
|
5卷引用:湖北省部分重点中学2023届高三上学期1月第二次联考数学试题
湖北省部分重点中学2023届高三上学期1月第二次联考数学试题湖北省恩施州高中教育联盟2023届高三上学期期末数学试题(已下线)第七章 随机变量及其分布(A卷·知识通关练)(1)(已下线)大题强化训练(5)(已下线)8.1 条件概率(含8.1.1-8.1.3)(练习)-2022-2023学年高二数学同步精品课堂(苏教版2019选择性必修第二册)
名校
8 . 随机变量的概念是俄国数学家切比雪夫在十九世纪中叶建立和提倡使用的.切比雪夫在数论、概率论、函数逼近论、积分学等方面均有所建树,他证明了如下以他名字命名的离散型切比雪夫不等式:设 为离散型随机变量,则
为离散型随机变量,则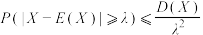 ,其中
,其中 为任意大于0的实数.切比雪夫不等式可以使人们在随机变量
为任意大于0的实数.切比雪夫不等式可以使人们在随机变量 的分布未知的情况下,对事件
的分布未知的情况下,对事件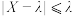 的概率作出估计.
的概率作出估计.
(1)证明离散型切比雪夫不等式;
(2)应用以上结论,回答下面问题:已知正整数 .在一次抽奖游戏中,有
.在一次抽奖游戏中,有 个不透明的箱子依次编号为
个不透明的箱子依次编号为 ,编号为
,编号为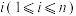 的箱子中装有编号为
的箱子中装有编号为 的
的 个大小、质地均相同的小球.主持人邀请
个大小、质地均相同的小球.主持人邀请 位嘉宾从每个箱子中随机抽取一个球,记从编号为
位嘉宾从每个箱子中随机抽取一个球,记从编号为 的箱子中抽取的小球号码为
的箱子中抽取的小球号码为 ,并记
,并记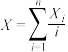 .对任意的
.对任意的 ,是否总能保证
,是否总能保证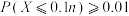 (假设嘉宾和箱子数能任意多)?并证明你的结论.
(假设嘉宾和箱子数能任意多)?并证明你的结论.
附:可能用到的公式(数学期望的线性性质):对于离散型随机变量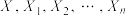 满足
满足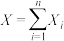 ,则有
,则有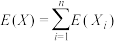 .
.
 为离散型随机变量,则
为离散型随机变量,则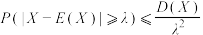 ,其中
,其中 为任意大于0的实数.切比雪夫不等式可以使人们在随机变量
为任意大于0的实数.切比雪夫不等式可以使人们在随机变量 的分布未知的情况下,对事件
的分布未知的情况下,对事件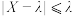 的概率作出估计.
的概率作出估计.(1)证明离散型切比雪夫不等式;
(2)应用以上结论,回答下面问题:已知正整数
 .在一次抽奖游戏中,有
.在一次抽奖游戏中,有 个不透明的箱子依次编号为
个不透明的箱子依次编号为 ,编号为
,编号为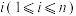 的箱子中装有编号为
的箱子中装有编号为 的
的 个大小、质地均相同的小球.主持人邀请
个大小、质地均相同的小球.主持人邀请 位嘉宾从每个箱子中随机抽取一个球,记从编号为
位嘉宾从每个箱子中随机抽取一个球,记从编号为 的箱子中抽取的小球号码为
的箱子中抽取的小球号码为 ,并记
,并记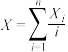 .对任意的
.对任意的 ,是否总能保证
,是否总能保证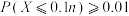 (假设嘉宾和箱子数能任意多)?并证明你的结论.
(假设嘉宾和箱子数能任意多)?并证明你的结论.附:可能用到的公式(数学期望的线性性质):对于离散型随机变量
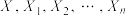 满足
满足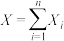 ,则有
,则有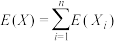 .
.
您最近一年使用:0次
2022-10-03更新
|
1921次组卷
|
7卷引用:湖北省二十一所重点中学2023届高三上学期第三次联考数学试题
湖北省二十一所重点中学2023届高三上学期第三次联考数学试题(已下线)专题10 概率与统计的综合运用(精讲精练)-1(已下线)7.3 离散型随机变量的数字特征(练习)-2022-2023学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)第二篇 函数与导数专题5 切比雪夫、帕德逼近 微点3 切比雪夫函数与切比雪夫不等式重庆市北碚区2023届高三上学期10月月度质量检测数学试题(已下线)每日一题 第15题 期望方差 回归定义(高三)(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大题型)(练习)
名校
9 . 某商场拟在周年店庆进行促销活动,对一次性消费超过200元的顾客,特别推出“玩游戏,送礼券”的活动,游戏规则如下:每轮游戏都抛掷一枚质地均匀的骰子,若向上点数不超过4点,获得1分,否则获得2分,进行若干轮游戏,若累计得分为9分,则游戏结束,可得到200元礼券,若累计得分为10分,则游戏结束,可得到纪念品一份,最多进行9轮游戏.
(1)当进行完3轮游戏时,总分为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(2)若累计得分为 的概率为
的概率为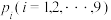 ,初始分数为0分,记
,初始分数为0分,记
(i)证明:数列 是等比数列;
是等比数列;
(ii)求活动参与者得到纪念品的概率.
(1)当进行完3轮游戏时,总分为
 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(2)若累计得分为
 的概率为
的概率为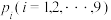 ,初始分数为0分,记
,初始分数为0分,记
(i)证明:数列
 是等比数列;
是等比数列;(ii)求活动参与者得到纪念品的概率.
您最近一年使用:0次
2022-05-10更新
|
1544次组卷
|
7卷引用:湖北省武汉市第四十九中学2022-2023学年高二下学期6月月考数学试题
湖北省武汉市第四十九中学2022-2023学年高二下学期6月月考数学试题山东省青岛市青岛大学附属中学2021-2022学年高二下学期期中数学试题第四章 概率与统计(B卷·能力提升练)-【单元测试】2022-2023学年高二数学分层训练AB卷(人教B版2019)浙江省宁波市奉化区九校联考2022-2023学年高二下学期期末模拟数学试题(已下线)第九章 综合测试B(基础卷)(已下线)考点19 概率中的数列 2024届高考数学考点总动员【练】浙江省台金七校联盟2023-2024学年高二下学期4月期中联考数学试题
10 . 由于全球新冠肺炎疫情呈高发态势,我国零星散发病例和局部地区聚集性疫情明显增加,为了全面抗击,做到网格化管理,要求在2021年1月28日至3月8日春运期间必须持新冠病毒核酸检测阴性证明才能出行.若甲、乙两人去 ,
, ,
, ,
, 四个医院中的一个做检测,则他们不在同一个医院做检测的概率为( )
四个医院中的一个做检测,则他们不在同一个医院做检测的概率为( )
 ,
, ,
, ,
, 四个医院中的一个做检测,则他们不在同一个医院做检测的概率为( )
四个医院中的一个做检测,则他们不在同一个医院做检测的概率为( )A. | B. | C. | D. |
您最近一年使用:0次
2021-07-07更新
|
673次组卷
|
5卷引用:湖北省腾云联盟2021-2022学年高三上学期10月联考数学试题
湖北省腾云联盟2021-2022学年高三上学期10月联考数学试题全国2021届高三高考数学(理)演练试题(一)(已下线)考点37 古典概型与几何概型-备战2022年高考数学(理)一轮复习考点微专题(已下线)考向44 排列、组合(已下线)模块综合练01概率与统计-2022年高考数学(理)一轮复习小题多维练(全国通用)