2020·安徽合肥·模拟预测
名校
解题方法
1 . 某单位为患病员工集体筛查新型流感病毒,需要去某医院检验血液是否为阳性,现有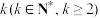 份血液样本,有以下两种检验方案,方案一:逐份检验,则需要检验k次;方案二:混合检验,将k份血液样本分别取样混合在一起检验一次,若检验结果为阴性,则k份血液样本均为阴性,若检验结果为阳性,为了确定k份血液中的阳性血液样本,则对k份血液样本再逐一检验.逐份检验和混合检验中的每一次检验费用都是
份血液样本,有以下两种检验方案,方案一:逐份检验,则需要检验k次;方案二:混合检验,将k份血液样本分别取样混合在一起检验一次,若检验结果为阴性,则k份血液样本均为阴性,若检验结果为阳性,为了确定k份血液中的阳性血液样本,则对k份血液样本再逐一检验.逐份检验和混合检验中的每一次检验费用都是 元,且k份血液样本混合检验一次需要额外收
元,且k份血液样本混合检验一次需要额外收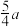 元的材料费和服务费.假设在接受检验的血液样本中,每份样本是否为阳性是相互独立的,且据统计每份血液样本是阳性的概率为
元的材料费和服务费.假设在接受检验的血液样本中,每份样本是否为阳性是相互独立的,且据统计每份血液样本是阳性的概率为 .
.
(1)若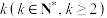 份血液样本采用混合检验方案,需要检验的总次数为X,求X分布列及数学期望;
份血液样本采用混合检验方案,需要检验的总次数为X,求X分布列及数学期望;
(2)①若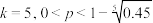 ,以检验总费用为决策依据,试说明该单位选择方案二的合理性;
,以检验总费用为决策依据,试说明该单位选择方案二的合理性;
②若 ,采用方案二总费用的数学期望低于方案一,求k的最大值.
,采用方案二总费用的数学期望低于方案一,求k的最大值.
参考数据: ,
, ,
, ,
, ,
,
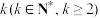 份血液样本,有以下两种检验方案,方案一:逐份检验,则需要检验k次;方案二:混合检验,将k份血液样本分别取样混合在一起检验一次,若检验结果为阴性,则k份血液样本均为阴性,若检验结果为阳性,为了确定k份血液中的阳性血液样本,则对k份血液样本再逐一检验.逐份检验和混合检验中的每一次检验费用都是
份血液样本,有以下两种检验方案,方案一:逐份检验,则需要检验k次;方案二:混合检验,将k份血液样本分别取样混合在一起检验一次,若检验结果为阴性,则k份血液样本均为阴性,若检验结果为阳性,为了确定k份血液中的阳性血液样本,则对k份血液样本再逐一检验.逐份检验和混合检验中的每一次检验费用都是 元,且k份血液样本混合检验一次需要额外收
元,且k份血液样本混合检验一次需要额外收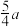 元的材料费和服务费.假设在接受检验的血液样本中,每份样本是否为阳性是相互独立的,且据统计每份血液样本是阳性的概率为
元的材料费和服务费.假设在接受检验的血液样本中,每份样本是否为阳性是相互独立的,且据统计每份血液样本是阳性的概率为 .
.(1)若
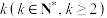 份血液样本采用混合检验方案,需要检验的总次数为X,求X分布列及数学期望;
份血液样本采用混合检验方案,需要检验的总次数为X,求X分布列及数学期望;(2)①若
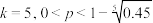 ,以检验总费用为决策依据,试说明该单位选择方案二的合理性;
,以检验总费用为决策依据,试说明该单位选择方案二的合理性;②若
 ,采用方案二总费用的数学期望低于方案一,求k的最大值.
,采用方案二总费用的数学期望低于方案一,求k的最大值.参考数据:
 ,
, ,
, ,
, ,
,
您最近一年使用:0次
2020-08-14更新
|
2778次组卷
|
7卷引用:第51讲 概率与统计综合问题-2022年新高考数学二轮专题突破精练
(已下线)第51讲 概率与统计综合问题-2022年新高考数学二轮专题突破精练(已下线)专题11-2 概率与分布列大题归类-1(已下线)模块十 计数原理与统计概率-2(已下线)专题9-1 概率与统计及分布列归类(理)(讲+练)-2安徽省合肥市第一中学2020届高三下学期最后一卷数学(理)试题河南省南阳市2020-2021学年高三上学期期末数学(理)试题河北省部分重点中学2022届高三下学期期中数学试题
18-19高三·湖南长沙·阶段练习
名校
2 . 据长期统计分析,某货物每天的需求量 在17与26之间,日需求量
在17与26之间,日需求量 (件)的频率
(件)的频率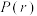 分布如下表所示:
分布如下表所示:
已知其成本为每件5元,售价为每件10元.若供大于求,则每件需降价处理,处理价每件2元.假设每天的进货量必需固定.
(1)设每天的进货量为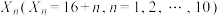 ,视日需求量
,视日需求量 的频率为概率
的频率为概率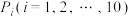 ,求在每天进货量为
,求在每天进货量为 的条件下,日销售量
的条件下,日销售量 的期望值
的期望值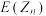 (用
(用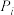 表示);
表示);
(2)在(1)的条件下,写出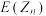 和
和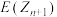 的关系式,并判断
的关系式,并判断 为何值时,日利润的均值最大?
为何值时,日利润的均值最大?
 在17与26之间,日需求量
在17与26之间,日需求量 (件)的频率
(件)的频率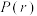 分布如下表所示:
分布如下表所示:需求量 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
频率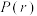 | 0.12 | 0.18 | 0.23 | 0.13 | 0.10 | 0.08 | 0.05 | 0.04 | 0.04 | 0.03 |
已知其成本为每件5元,售价为每件10元.若供大于求,则每件需降价处理,处理价每件2元.假设每天的进货量必需固定.
(1)设每天的进货量为
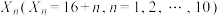 ,视日需求量
,视日需求量 的频率为概率
的频率为概率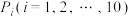 ,求在每天进货量为
,求在每天进货量为 的条件下,日销售量
的条件下,日销售量 的期望值
的期望值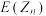 (用
(用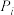 表示);
表示);(2)在(1)的条件下,写出
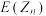 和
和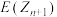 的关系式,并判断
的关系式,并判断 为何值时,日利润的均值最大?
为何值时,日利润的均值最大?
您最近一年使用:0次
18-19高二下·河南平顶山·期末
3 . 设 ,
, ,
, ,将
,将 的最小值记为
的最小值记为 .则当
.则当 是偶数时,
是偶数时,
__________ ;当 是奇数时,
是奇数时,
__________ .
 ,
, ,
, ,将
,将 的最小值记为
的最小值记为 .则当
.则当 是偶数时,
是偶数时,
 是奇数时,
是奇数时,
您最近一年使用:0次
4 . 设整数数列{an}共有2n(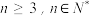 )项,满足
)项,满足 ,
, ,且
,且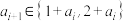 (
( ).
).
(1)当 时,写出满足条件的数列的个数;
时,写出满足条件的数列的个数;
(2)当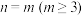 时,求满足条件的数列的个数.
时,求满足条件的数列的个数.
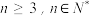 )项,满足
)项,满足 ,
, ,且
,且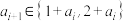 (
( ).
).(1)当
 时,写出满足条件的数列的个数;
时,写出满足条件的数列的个数;(2)当
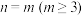 时,求满足条件的数列的个数.
时,求满足条件的数列的个数.
您最近一年使用:0次
2019-03-22更新
|
1186次组卷
|
3卷引用:专题11.1 计数原理(练)-江苏版《2020年高考一轮复习讲练测》



