名校
1 . 调味品品评师的重要工作是对各种品牌的调味品进行品尝,分析、鉴定,调配、研发,周而复始、反复对比.对调味品品评师考核测试的一种常用方法如下:拿出n瓶外观相同但品质不同的调味品让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这n瓶调味品,并重新按品质优劣为它们排序,这称为一轮测试.根据一轮测试中的两次排序的偏离程度的高低为其评分.现设 ,分别以
,分别以 ,
, ,
, ,
, 表示第一次排序时被排为1,2,3,4的四种调味品在第二次排序时的序号,并令
表示第一次排序时被排为1,2,3,4的四种调味品在第二次排序时的序号,并令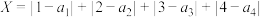 ,则X是对两次排序的偏离程度的一种描述.(如第二次排序时的序号为1,3,2,4,则
,则X是对两次排序的偏离程度的一种描述.(如第二次排序时的序号为1,3,2,4,则 ).
).
(1)写出X的所有可能值构成的集合;
(2)假设 ,
, ,
,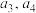 的排列等可能地为1,2,3,4的各种排列,求X的数学期望;
的排列等可能地为1,2,3,4的各种排列,求X的数学期望;
(3)某调味品品评师在相继进行的三轮测试中,都有 .
.
(i)试按(2)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);
(ⅱ)请你判断该调味品品评师的品味鉴别能力如何?并说明理由.
 ,分别以
,分别以 ,
, ,
, ,
, 表示第一次排序时被排为1,2,3,4的四种调味品在第二次排序时的序号,并令
表示第一次排序时被排为1,2,3,4的四种调味品在第二次排序时的序号,并令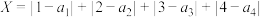 ,则X是对两次排序的偏离程度的一种描述.(如第二次排序时的序号为1,3,2,4,则
,则X是对两次排序的偏离程度的一种描述.(如第二次排序时的序号为1,3,2,4,则 ).
).(1)写出X的所有可能值构成的集合;
(2)假设
 ,
, ,
,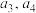 的排列等可能地为1,2,3,4的各种排列,求X的数学期望;
的排列等可能地为1,2,3,4的各种排列,求X的数学期望;(3)某调味品品评师在相继进行的三轮测试中,都有
 .
.(i)试按(2)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);
(ⅱ)请你判断该调味品品评师的品味鉴别能力如何?并说明理由.
您最近一年使用:0次
2020-04-12更新
|
387次组卷
|
4卷引用:2020届河北省石家庄市第二中学高三一模教学质量检测数学(理)试题
2020届河北省石家庄市第二中学高三一模教学质量检测数学(理)试题2020届山东省潍坊五县联合模拟考试数学试题(已下线)必刷卷04-2021年高考数学考前信息必刷卷(新高考地区专用)(已下线)黄金卷12-【赢在高考·黄金20卷】备战2021年高考数学全真模拟卷(江苏专用)
2 . 某药物研究所为了研究小白鼠的身长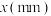 与体重
与体重 的关系,随机抽测了20只小白鼠,得到如下数据:
的关系,随机抽测了20只小白鼠,得到如下数据:
(1)若从序号为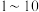 的10只小白鼠中任取2只,其中序号是5的倍数的小白鼠个数为
的10只小白鼠中任取2只,其中序号是5的倍数的小白鼠个数为 ,求
,求 的分布列与数学期望;
的分布列与数学期望;
(2)请根据序号为5的倍数的几组数据,求出 关于
关于 的经验回归方程(精确到0.01).
的经验回归方程(精确到0.01).
附:经验回归方程 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为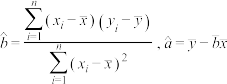 .
.
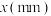 与体重
与体重 的关系,随机抽测了20只小白鼠,得到如下数据:
的关系,随机抽测了20只小白鼠,得到如下数据:| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
身长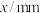 | 113 | 88 | 91 | 96 | 97 | 79 | 91 | 87 | 88 | 85 |
体重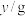 | 39 | 31 | 35 | 33 | 34 | 36 | 42 | 39 | 40 | 39 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
身长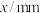 | 89 | 98 | 87 | 94 | 103 | 99 | 85 | 90 | 82 | 91 |
体重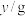 | 41 | 43 | 40 | 43 | 37 | 32 | 38 | 41 | 37 | 42 |
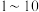 的10只小白鼠中任取2只,其中序号是5的倍数的小白鼠个数为
的10只小白鼠中任取2只,其中序号是5的倍数的小白鼠个数为 ,求
,求 的分布列与数学期望;
的分布列与数学期望;(2)请根据序号为5的倍数的几组数据,求出
 关于
关于 的经验回归方程(精确到0.01).
的经验回归方程(精确到0.01).附:经验回归方程
 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为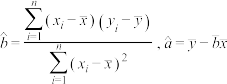 .
.
您最近一年使用:0次
解题方法
3 . 某民营学校为增强实力与影响力,大力招揽名师、建设校园硬件设施,近5年该校招生人数的数据如下表:
(1)由表中数据可看出,可用线性回归模型拟合 与
与 的关系,请用相关系数加以证明;
的关系,请用相关系数加以证明;
(2)求 关于
关于 的回归直线方程,并预测当年份序号为7时该校的招生人数.
的回归直线方程,并预测当年份序号为7时该校的招生人数.
参考数据: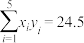 ,
, ,
, .
.
参考公式:相关系数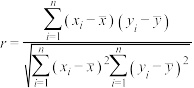 ,回归方程
,回归方程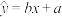 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为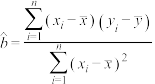 ,
, .
.
年份序号x | 1 | 2 | 3 | 4 | 5 |
招生人数y/千人 | 0.8 | 1 | 1.3 | 1.7 | 2.2 |
 与
与 的关系,请用相关系数加以证明;
的关系,请用相关系数加以证明;(2)求
 关于
关于 的回归直线方程,并预测当年份序号为7时该校的招生人数.
的回归直线方程,并预测当年份序号为7时该校的招生人数.参考数据:
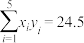 ,
, ,
, .
.参考公式:相关系数
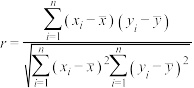 ,回归方程
,回归方程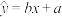 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为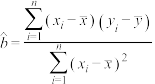 ,
, .
.
您最近一年使用:0次
2024-03-21更新
|
1046次组卷
|
6卷引用:河北省邯郸市2024届高三第三次调研考试考试数学试题
河北省邯郸市2024届高三第三次调研考试考试数学试题河南省南阳市华龙高级中学2023-2024学年高二下学期3月月考数学试题(已下线)专题8.5 成对数据的统计分析全章十一大基础题型归纳(基础篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)专题8.4 统计分析大题专项训练【六大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)陕西省宝鸡市2024届高三下学期高考模拟检测(三)理科数学试题陕西省宝鸡市2024届高三下学期高考模拟检测(三)文科数学试题
名校
4 . 在科技飞速发展的今天,人工智能领域迎来革命性的突破.类似于OpenAI的人工智能大模型不仅具有高度智能化、自主化和自适应的特点,它们的学习能力和信息储存能力也远远超越人类,更是拥有强大的语音识别和语言理解能力.某机构分别用 ,
, 两种人工智能大模型进行对比研究,检验这两种大模型在答题时哪种更可靠,从某知识领域随机选取180个问题进行分组回答,其中
两种人工智能大模型进行对比研究,检验这两种大模型在答题时哪种更可靠,从某知识领域随机选取180个问题进行分组回答,其中 人工智能大模型回答100个问题,有90个正确;
人工智能大模型回答100个问题,有90个正确; 人工智能大模型回答剩下的80个问题,有65个正确.
人工智能大模型回答剩下的80个问题,有65个正确.
(1)完成下列 列联表,并根据小概率值
列联表,并根据小概率值 的
的 独立性检验,能否判断人工智能大模型的选择和回答正确有关?
独立性检验,能否判断人工智能大模型的选择和回答正确有关?
(2)将频率视为概率,用 人工智能大模型回答该知识领域的3道题目,且各题回答正确与否,相互之间没有影响,设回答题目正确的个数为
人工智能大模型回答该知识领域的3道题目,且各题回答正确与否,相互之间没有影响,设回答题目正确的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
参考公式及参考数据: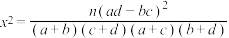 ,
, .
.
 ,
, 两种人工智能大模型进行对比研究,检验这两种大模型在答题时哪种更可靠,从某知识领域随机选取180个问题进行分组回答,其中
两种人工智能大模型进行对比研究,检验这两种大模型在答题时哪种更可靠,从某知识领域随机选取180个问题进行分组回答,其中 人工智能大模型回答100个问题,有90个正确;
人工智能大模型回答100个问题,有90个正确; 人工智能大模型回答剩下的80个问题,有65个正确.
人工智能大模型回答剩下的80个问题,有65个正确.(1)完成下列
 列联表,并根据小概率值
列联表,并根据小概率值 的
的 独立性检验,能否判断人工智能大模型的选择和回答正确有关?
独立性检验,能否判断人工智能大模型的选择和回答正确有关?| 回答正确 | 回答错误 | 合计 | |
 人工智能大模型 人工智能大模型 | |||
 人工智能大模型 人工智能大模型 | |||
| 合计 |
 人工智能大模型回答该知识领域的3道题目,且各题回答正确与否,相互之间没有影响,设回答题目正确的个数为
人工智能大模型回答该知识领域的3道题目,且各题回答正确与否,相互之间没有影响,设回答题目正确的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.参考公式及参考数据:
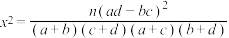 ,
, .
.
| 0.15 | 0.10 | 0.05 | 0.010 |
| 2.072 | 2.706 | 3.841 | 6.635 |
您最近一年使用:0次
2024-05-03更新
|
978次组卷
|
6卷引用:河北省邢台市南宫中学2023-2024学年高三高考考前定心卷2数学试题
河北省邢台市南宫中学2023-2024学年高三高考考前定心卷2数学试题贵州省凯里市第一中学2024届高三模拟考试(二模)数学试题(已下线)情境2 最新科技前沿(已下线)高二期末模拟卷02(已下线)专题04 第八章 成对数据的统计分析--高二期末考点大串讲(人教A版2019)湖北省宜昌市远安县第一高级中学2023-2024学年高二下学期5月月考数学试卷
名校
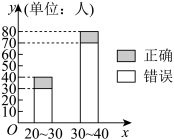
5 . “开门大吉”是某电视台推出的游戏益智节目.选手面对1﹣4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金(奖金金额累加),但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否人数如图所示.
每扇门对应的梦想基金:(单位:元)
(1)写出2×2列联表;判断是否有90%的把握认为猜对歌曲名称与否与年龄有关?说明你的理由.(下面的临界值表供参考)
(2)若某选手能正确回答第一、二、三、四扇门的概率分别为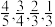 正确回答一个问题后,选择继续回答下一个问题的概率是
正确回答一个问题后,选择继续回答下一个问题的概率是 ,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为ξ,求ξ的分布列及数学期望(精确到0.01).(参考公式
,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为ξ,求ξ的分布列及数学期望(精确到0.01).(参考公式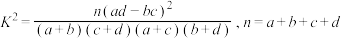 )
)

每扇门对应的梦想基金:(单位:元)
第一扇门 | 第二扇门 | 第三扇门 | 第四扇门 |
1000 | 2000 | 3000 | 5000 |
(1)写出2×2列联表;判断是否有90%的把握认为猜对歌曲名称与否与年龄有关?说明你的理由.(下面的临界值表供参考)
P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)若某选手能正确回答第一、二、三、四扇门的概率分别为
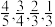 正确回答一个问题后,选择继续回答下一个问题的概率是
正确回答一个问题后,选择继续回答下一个问题的概率是 ,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为ξ,求ξ的分布列及数学期望(精确到0.01).(参考公式
,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为ξ,求ξ的分布列及数学期望(精确到0.01).(参考公式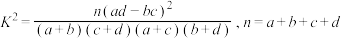 )
)
您最近一年使用:0次
2024-02-05更新
|
331次组卷
|
3卷引用:河北省衡水市冀州中学2024届高三上学期一轮复习效果验收数学试题(二)





