名校
解题方法
1 . 新冠疫情不断反弹,各大商超多措并举确保市民生活货品不断档,超市员工加班加点工作.某大型超市为答谢各位员工一年来的锐意进取和辛勤努力,拟在年会后,通过摸球兑奖的方式对500位员工进行奖励,规定:每位员工从一个装有5种面值奖券的箱子中,一次随机摸出2张奖券,奖券上所标的面值之和就是该员工所获得的奖励额.
(1)若箱子中所装的5种面值的奖券中有2张面值为100元,其余3张均为50元,试比较员工获得100元奖励额与获得150元奖励额的概率的大小;
(2)公司对奖励总额的预算是7万元,预定箱子中所装的5种面值的奖券有两种方案:第一方案是3张面值30元和2张面值130元;第二方案是3张面值50元和2张面值100元.为了使员工得到的奖励总额尽可能地符合公司的预算且每位员工所获得的奖励额相对均衡,请问选择哪一种方案比较好?并说明理由.
(1)若箱子中所装的5种面值的奖券中有2张面值为100元,其余3张均为50元,试比较员工获得100元奖励额与获得150元奖励额的概率的大小;
(2)公司对奖励总额的预算是7万元,预定箱子中所装的5种面值的奖券有两种方案:第一方案是3张面值30元和2张面值130元;第二方案是3张面值50元和2张面值100元.为了使员工得到的奖励总额尽可能地符合公司的预算且每位员工所获得的奖励额相对均衡,请问选择哪一种方案比较好?并说明理由.
您最近一年使用:0次
2023-04-14更新
|
721次组卷
|
9卷引用:山东省德州市2022-2023学年高二上学期期末数学试题
山东省德州市2022-2023学年高二上学期期末数学试题(已下线)模块一 专题2 概率统计 (人教B)(已下线)模块三 专题5 概率与统计--拔高能力练(人教B版)福建省宁德市寿宁县第一中学2022-2023学年高二下学期第二阶段考试(5月)数学试题江苏省连云港高级中学2022-2023学年高二下学期期中数学试题(已下线)拓展二:离散型随机变量的分布列与数字特征11种常见考法归类(2)(已下线)第10讲 离散型随机变量的均值与方差-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)(已下线)专题03 条件概率与全概率公式(3)(已下线)高二下学期期末复习解答题压轴题二十二大题型专练(5)
名校
2 . 某公司全年圆满完成预定的生产任务,为答谢各位员工一年来的锐意进取和辛勤努力,公司决定在联欢晚会后,拟通过摸球兑奖的方式对500位员工进行奖励,规定:每位员工从一个装有4种面值的奖券的箱子中,一次随机摸出2张奖券,奖券上所标的面值之和就是该员工所获得的奖励额.
(1)若箱子中所装的4种面值的奖券中有1张面值为80元,其余3张均为40元,试比较员工获得80元奖励额与获得120元奖励额的概率的大小;
(2)公司对奖励总额的预算是6万元,预定箱子中所装的4种面值的奖券有两种方案:第一方案是2张面值20元和2张面值100元;第二方案是2张面值40元和2张面值80元.为了使员工得到的奖励总额尽可能地符合公司的预算且每位员工所获得的奖励额相对均衡,请问选择哪一种方案比较好?并说明理由.
(1)若箱子中所装的4种面值的奖券中有1张面值为80元,其余3张均为40元,试比较员工获得80元奖励额与获得120元奖励额的概率的大小;
(2)公司对奖励总额的预算是6万元,预定箱子中所装的4种面值的奖券有两种方案:第一方案是2张面值20元和2张面值100元;第二方案是2张面值40元和2张面值80元.为了使员工得到的奖励总额尽可能地符合公司的预算且每位员工所获得的奖励额相对均衡,请问选择哪一种方案比较好?并说明理由.
您最近一年使用:0次
2022-02-27更新
|
2368次组卷
|
10卷引用:山东省大教育联盟学校2021-2022学年高三下学期收心考试(开学考试)数学试题
山东省大教育联盟学校2021-2022学年高三下学期收心考试(开学考试)数学试题(已下线)技巧04 解答题解法与技巧(练)--第二篇 解题技巧篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》重庆市万州第二高级中学2021-2022学年高二下学期期中数学试题福建省厦门集美中学2021-2022学年高二下学期期中考试数学试题重庆市万州纯阳中学校2021-2022学年高二下学期期中数学(A卷)试题(已下线)第06讲 离散型随机变量的均值与方差(核心考点讲与练)-2021-2022学年高二数学下学期考试满分全攻略(人教A版2019选修第二册+第三册)(已下线)第07讲 离散型随机变量及其分布列和数字特征 (精讲)上海市延安中学2023届高三下学期开学考试数学试题(已下线)第七章 随机变量及其分布 全章总结 (精讲)(2)上海市曹杨第二中学2023届高三三模数学试题
解题方法
3 . 高二(16)班参加青华中学红五月节目:猜歌名,班级只有一个名额,结合平时观察积累,闫某峻,贾某轩两名学生进入最后选拔,申老师为此设计了如下选拔方案:挑选8首歌进行测试,在这8首歌曲中,闫某峻能正确说出其中的6首歌名,贾某轩能正确说出每首歌名的概率均为 ,假设闫某峻、贾某轩两名学生说出每首歌名都相互独立、互不影响,现闫某峻、贾某轩从这8首歌中分别随机抽取4首进行竞猜
,假设闫某峻、贾某轩两名学生说出每首歌名都相互独立、互不影响,现闫某峻、贾某轩从这8首歌中分别随机抽取4首进行竞猜
(1)求闫某峻、贾某轩共答对3首歌名的概率;
(2)从数学期望和方差的角度分析,应选拔哪个学生代表高二(16)班参加红五月活动?
 ,假设闫某峻、贾某轩两名学生说出每首歌名都相互独立、互不影响,现闫某峻、贾某轩从这8首歌中分别随机抽取4首进行竞猜
,假设闫某峻、贾某轩两名学生说出每首歌名都相互独立、互不影响,现闫某峻、贾某轩从这8首歌中分别随机抽取4首进行竞猜(1)求闫某峻、贾某轩共答对3首歌名的概率;
(2)从数学期望和方差的角度分析,应选拔哪个学生代表高二(16)班参加红五月活动?
您最近一年使用:0次
名校
4 . 2023年五一劳动节前夕,某公司为全体员工发放奖励,奖励拟采用抽签方式发放:每位员工分别从标有不同面值的4张卡片中随机取出2张,2张卡片上的面值之和即为该员工的奖励金额.
(1)若4张卡片上的面值分别为100元,100元,300元,500元.
①求每位员工所获得的奖励金额不低于500元的概率;
②记每位员工所获得的奖励金额为X元,求X的分布列与期望;
(2)你能否设计一种抽签方案,使得4张卡片上的面值分别为100元,200元,300元,400元,500元中的3个,且每位员工所获得的奖励金额的期望值不变,且奖励金额相对均衡(只需给出一种方案并说明理由即可,不需要判断是否还有其他方案).
(1)若4张卡片上的面值分别为100元,100元,300元,500元.
①求每位员工所获得的奖励金额不低于500元的概率;
②记每位员工所获得的奖励金额为X元,求X的分布列与期望;
(2)你能否设计一种抽签方案,使得4张卡片上的面值分别为100元,200元,300元,400元,500元中的3个,且每位员工所获得的奖励金额的期望值不变,且奖励金额相对均衡(只需给出一种方案并说明理由即可,不需要判断是否还有其他方案).
您最近一年使用:0次
名校
解题方法
5 . 某校设计了一个实验学科的实验考查方案;考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作,规定:至少正确完成两题便可通过,已知6道备选题中甲生有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是 ,求:
,求:
(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(2)试用统计知识分析比较两考生的实验操作能力.
 ,求:
,求:(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(2)试用统计知识分析比较两考生的实验操作能力.
您最近一年使用:0次
名校
解题方法
6 . 我市拟建立一个博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从6个招标问题中随机抽取3个问题,已知这6个招标问题中,甲公司能正确回答其中4道题目,而乙公司能正确回答每道题目的概率均为  ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
(1)求甲公司至少答对2道题目的概率;
(2)分别求甲、乙两家公司答对题数的分布列,请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
 ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.(1)求甲公司至少答对2道题目的概率;
(2)分别求甲、乙两家公司答对题数的分布列,请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
您最近一年使用:0次
2024-05-31更新
|
1034次组卷
|
4卷引用:内蒙古自治区赤峰市红山区赤峰第四中学分校2023-2024学年高二下学期5月期中数学试题
内蒙古自治区赤峰市红山区赤峰第四中学分校2023-2024学年高二下学期5月期中数学试题(已下线)专题04 随机变量及其分布类常考题型归类--高二期末考点大串讲(人教B版2019选择性必修第二册)(已下线)高二数学下学期期末押题--高二期末考点大串讲(苏教版2019选择性必修第二册)天津市第一中学2023-2024学年高二下学期期末质量调查数学试卷
7 . 某学校参加某项竞赛仅有一个名额,结合平时训练成绩,甲、乙两名学生进入最后选拔,学校为此设计了如下选拔方案:设计6道题进行测试,若这6道题中,甲能正确解答其中的4道,乙能正确解答每个题目的概率均为 ,假设甲、乙两名学生解答每道测试题都相互独立、互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答
,假设甲、乙两名学生解答每道测试题都相互独立、互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答
(1)求甲、乙共答对2道题目的概率;
(2)设甲答对题数为随机变量X,求X的分布列、数学期望和方差;
(3)从数学期望和方差的角度分析,应选拔哪个学生代表学校参加竞赛?
 ,假设甲、乙两名学生解答每道测试题都相互独立、互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答
,假设甲、乙两名学生解答每道测试题都相互独立、互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答(1)求甲、乙共答对2道题目的概率;
(2)设甲答对题数为随机变量X,求X的分布列、数学期望和方差;
(3)从数学期望和方差的角度分析,应选拔哪个学生代表学校参加竞赛?
您最近一年使用:0次
2024-04-02更新
|
2608次组卷
|
10卷引用:广东省东莞市东华高级中学2022-2023学年高二下学期期中考试数学试卷
广东省东莞市东华高级中学2022-2023学年高二下学期期中考试数学试卷(已下线)高二下学期期中模拟卷(新题型)(导数+计数原理+随机变量及其分布+统计)-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)(已下线)第七章:随机变量及其分布章末重点题型复习(7题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)吉林省长春市第五中学2023-2024年高二下学期第二学程数学试题四川省眉山市彭山区第一中学2023-2024学年高二下学期5月月考数学试题河北省承德市2023-2024学年高二年级下学期5月联考数学试题(已下线)专题01 高二下期末真题精选(2)--高二期末考点大串讲(人教A版2019)四川省仁寿第一中学校(北校区)2023-2024学年高二下学期7月期末考试数学试题青海省西宁市海湖中学2023-2024学年高二下学期第二阶段考试数学试卷江苏省扬州市仪征市精诚高级中学2023-2024学年高二下学期5月月考数学试题
解题方法
8 . 根据历史资料显示,某种慢性疾病患者的自然痊愈率为5%.为试验一种新药,在有关部门批准后,医院将此药给10位病人服用,试验方案为:若这10人中至少有2人痊愈,则认为该药有效,提高了治愈率;否则,则认为该药无效.
(1)如果在该次试验中有5人痊愈,院方欲从参加该次试验的10人中随机选2人了解服药期间的感受,记抽到痊愈的人的个数为X,求X的概率分布.
(2)在第(1)题的条件下求随机变量X的期望与方差.
(3)如果新药有效,将治愈率提高到了50%,求通过试验却认定新药无效的概率P并根据P的值解释该试验方案的合理性.(参考结论:通常认为发生概率小于5%的事件可视为小概率事件).
(1)如果在该次试验中有5人痊愈,院方欲从参加该次试验的10人中随机选2人了解服药期间的感受,记抽到痊愈的人的个数为X,求X的概率分布.
(2)在第(1)题的条件下求随机变量X的期望与方差.
(3)如果新药有效,将治愈率提高到了50%,求通过试验却认定新药无效的概率P并根据P的值解释该试验方案的合理性.(参考结论:通常认为发生概率小于5%的事件可视为小概率事件).
您最近一年使用:0次
9 . 某校设计了一个实验学科的实验考查方案;考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作,规定:至少正确完成其中2题便可通过.已知6道备选题中考生甲有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是 ,且每题正确完成与否互不影响,求:
,且每题正确完成与否互不影响,求:
(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(2)试用统计知识分析比较两考生的实验操作能力.
 ,且每题正确完成与否互不影响,求:
,且每题正确完成与否互不影响,求:(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(2)试用统计知识分析比较两考生的实验操作能力.
您最近一年使用:0次
2023-11-24更新
|
1246次组卷
|
6卷引用:北京市西城区北师大二附中2024届高三上学期期中数学试题
北京市西城区北师大二附中2024届高三上学期期中数学试题(已下线)模块二 专题3 概率与统计中决策问题(已下线)6.4.2超几何分布(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)(已下线)专题04 随机变量的均值与方差综合--高二期末考点大串讲(人教B版2019选择性必修第二册)(已下线)专题7 期望方差 定义性质(经典好题母题)【练】(已下线)第三章 随机变量及其分布列 专题四 随机变量分布列、期望、方差的应用 微点5 概率分布在生活、生产实践中的应用综合训练【培优版】
名校
解题方法
10 . 我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了抽样调查,得到该市100位居民的月均用水量(单位:吨),将数据按照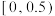 ,
, ,…,
,…,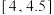 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
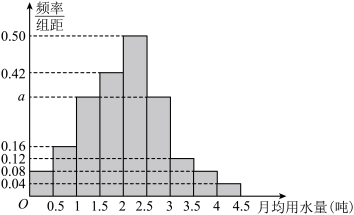
(1)现从这100位居民中月均用水量在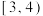 的人中,随机抽取4人进行电话回访,求至少有2人月均用水量在
的人中,随机抽取4人进行电话回访,求至少有2人月均用水量在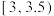 的概率;
的概率;
(2)把这100位居民的月均用水量的频率视为该市居民的月均用水量的概率,现从该市随机抽取1位,用 表示月均用水量不低于
表示月均用水量不低于 吨的人数,求
吨的人数,求 的期望和方差.
的期望和方差.
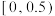 ,
, ,…,
,…,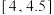 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)现从这100位居民中月均用水量在
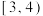 的人中,随机抽取4人进行电话回访,求至少有2人月均用水量在
的人中,随机抽取4人进行电话回访,求至少有2人月均用水量在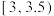 的概率;
的概率;(2)把这100位居民的月均用水量的频率视为该市居民的月均用水量的概率,现从该市随机抽取1位,用
 表示月均用水量不低于
表示月均用水量不低于 吨的人数,求
吨的人数,求 的期望和方差.
的期望和方差.
您最近一年使用:0次



