名校
1 . 某公司全年圆满完成预定的生产任务,为答谢各位员工一年来的锐意进取和辛勤努力,公司决定在联欢晚会后,拟通过摸球兑奖的方式对500位员工进行奖励,规定:每位员工从一个装有4种面值的奖券的箱子中,一次随机摸出2张奖券,奖券上所标的面值之和就是该员工所获得的奖励额.
(1)若箱子中所装的4种面值的奖券中有1张面值为80元,其余3张均为40元,试比较员工获得80元奖励额与获得120元奖励额的概率的大小;
(2)公司对奖励总额的预算是6万元,预定箱子中所装的4种面值的奖券有两种方案:第一方案是2张面值20元和2张面值100元;第二方案是2张面值40元和2张面值80元.为了使员工得到的奖励总额尽可能地符合公司的预算且每位员工所获得的奖励额相对均衡,请问选择哪一种方案比较好?并说明理由.
(1)若箱子中所装的4种面值的奖券中有1张面值为80元,其余3张均为40元,试比较员工获得80元奖励额与获得120元奖励额的概率的大小;
(2)公司对奖励总额的预算是6万元,预定箱子中所装的4种面值的奖券有两种方案:第一方案是2张面值20元和2张面值100元;第二方案是2张面值40元和2张面值80元.为了使员工得到的奖励总额尽可能地符合公司的预算且每位员工所获得的奖励额相对均衡,请问选择哪一种方案比较好?并说明理由.
您最近一年使用:0次
2022-02-27更新
|
2368次组卷
|
10卷引用:山东省大教育联盟学校2021-2022学年高三下学期收心考试(开学考试)数学试题
山东省大教育联盟学校2021-2022学年高三下学期收心考试(开学考试)数学试题(已下线)技巧04 解答题解法与技巧(练)--第二篇 解题技巧篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》(已下线)第07讲 离散型随机变量及其分布列和数字特征 (精讲)上海市延安中学2023届高三下学期开学考试数学试题上海市曹杨第二中学2023届高三三模数学试题重庆市万州第二高级中学2021-2022学年高二下学期期中数学试题福建省厦门集美中学2021-2022学年高二下学期期中考试数学试题重庆市万州纯阳中学校2021-2022学年高二下学期期中数学(A卷)试题(已下线)第06讲 离散型随机变量的均值与方差(核心考点讲与练)-2021-2022学年高二数学下学期考试满分全攻略(人教A版2019选修第二册+第三册)(已下线)第七章 随机变量及其分布 全章总结 (精讲)(2)
2024高三·全国·专题练习
名校
2 . 某短视频软件经过几年的快速发展,深受人们的喜爱,该软件除了有娱乐属性外,也可通过平台推送广告.某公司为了宣传新产品,现有以下两种宣传方案:
方案一:投放该平台广告,据市场调研,其收益X分别为0元,20万元,40万元,且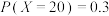 ,期望
,期望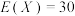 .
.
方案二:投放传统广告,据市场调研,其收益Y分别为10万元,20万元,30万元,其概率依次为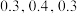 .
.
(1)请写出方案一的分布列,并求方差 ;
;
(2)请你根据所学的统计知识给出建议,该公司宣传应该投放哪种广告?并说明你的理由.
方案一:投放该平台广告,据市场调研,其收益X分别为0元,20万元,40万元,且
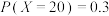 ,期望
,期望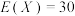 .
.方案二:投放传统广告,据市场调研,其收益Y分别为10万元,20万元,30万元,其概率依次为
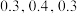 .
.(1)请写出方案一的分布列,并求方差
 ;
;(2)请你根据所学的统计知识给出建议,该公司宣传应该投放哪种广告?并说明你的理由.
您最近一年使用:0次
2024-01-07更新
|
727次组卷
|
7卷引用:专题02 结论探索型【练】【北京版】
(已下线)专题02 结论探索型【练】【北京版】(已下线)7.3.2离散型随机变量的方差(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)专题7.7 随机变量及其分布全章十一大基础题型归纳(基础篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)第09讲 第七章随机变量及其分布章末题型大总结-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)广东省东莞市七校2023-2024学年高二下学期5月联考数学试题陕西省咸阳市武功县普集高级中学2023-2024学年高二下学期6月月考数学试题(已下线)专题03 第七章 随机变量及其分布列--高二期末考点大串讲(人教A版2019)
3 . 某公司举办公司员工联欢晩会,为活跃气氛,计划举行摸奖活动,有两种方案:
方案一:不放回从装有 个红球和
个红球和 个白球的箱子中随机摸出
个白球的箱子中随机摸出 个球,每摸出一红球奖励
个球,每摸出一红球奖励 元:
元:
方案二:有放回从装有 个红球和
个红球和 个白球的箱子中随机摸出
个白球的箱子中随机摸出 个球,每摸出一红球奖励
个球,每摸出一红球奖励 元,分别用随机变量
元,分别用随机变量 、
、 表示某员工按方案一和方案二抽奖的获奖金额.
表示某员工按方案一和方案二抽奖的获奖金额.
(1)求随机变量 的分布列和数学期望:
的分布列和数学期望:
(2)用统计知识分析,为使公司员工获奖金额相对均衡,应选择哪种方案?请说明理由.
方案一:不放回从装有
 个红球和
个红球和 个白球的箱子中随机摸出
个白球的箱子中随机摸出 个球,每摸出一红球奖励
个球,每摸出一红球奖励 元:
元:方案二:有放回从装有
 个红球和
个红球和 个白球的箱子中随机摸出
个白球的箱子中随机摸出 个球,每摸出一红球奖励
个球,每摸出一红球奖励 元,分别用随机变量
元,分别用随机变量 、
、 表示某员工按方案一和方案二抽奖的获奖金额.
表示某员工按方案一和方案二抽奖的获奖金额.(1)求随机变量
 的分布列和数学期望:
的分布列和数学期望:(2)用统计知识分析,为使公司员工获奖金额相对均衡,应选择哪种方案?请说明理由.
您最近一年使用:0次
2023-07-09更新
|
453次组卷
|
6卷引用:模块二 专题3 概率与统计中决策问题
(已下线)模块二 专题3 概率与统计中决策问题福建省南平市2022-2023学年高二下学期期末考试数学试题(已下线)4.2.4 随机变量的数字特征(第2课时) 离散型随机变量的方差(分层练习)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第二册)(已下线)2023-2024学年高二下学期期中复习解答题压轴题十七大题型专练(2)(已下线)7.3.2 离散型随机变量的方差——课后作业(提升版)(已下线)专题04 随机变量的均值与方差综合--高二期末考点大串讲(人教B版2019选择性必修第二册)
4 . 为切实做好新冠疫情防控工作,有效、及时地控制和消除新冠肺炎的危害,增加学生对新冠肺炎预防知识的了解,某校举办了一次“新冠疫情”知识竞赛.竞赛分个人赛和团体赛两种.个人赛参赛方式为:组委会采取电脑出题的方式,从题库中随机出10道题,编号为 ,
, ,
, ,
, ,
, ,
,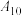 ,电脑依次出题,参赛选手按规则作答,每答对一道题得10分,答错得0分.团体赛以班级为单位,各班参赛人数必须为3的倍数,且不少于18人,团体赛分预赛和决赛两个阶段,其中预赛阶段各班可从以下两种参赛方案中任选一种参赛:
,电脑依次出题,参赛选手按规则作答,每答对一道题得10分,答错得0分.团体赛以班级为单位,各班参赛人数必须为3的倍数,且不少于18人,团体赛分预赛和决赛两个阶段,其中预赛阶段各班可从以下两种参赛方案中任选一种参赛:
方案一:将班级选派的 名参赛选手每3人一组,分成
名参赛选手每3人一组,分成 组,电脑随机分配给同一组的3名选手一道相同的试题,3人均独立答题,若这3人中至少有2人回答正确,则该小组顺利出线;若这
组,电脑随机分配给同一组的3名选手一道相同的试题,3人均独立答题,若这3人中至少有2人回答正确,则该小组顺利出线;若这 个小组都顺利出线,则该班级晋级决赛.
个小组都顺利出线,则该班级晋级决赛.
方案二:将班级选派的 名参赛选手每
名参赛选手每 人一组,分成3组,电脑随机分配给同一组的
人一组,分成3组,电脑随机分配给同一组的 名选手一道相同的试题,每人均独立答题,若这
名选手一道相同的试题,每人均独立答题,若这 个人都回答正确,则该小组顺利出线;若这3个小组中至少有2个小组顺利出线,则该班级晋级决赛.
个人都回答正确,则该小组顺利出线;若这3个小组中至少有2个小组顺利出线,则该班级晋级决赛.
(1)郭靖同学参加了个人赛,已知郭靖同学答对题库中每道题的概率均为 ,每次作答结果相互独立,且他不会主动放弃任何一次作答机会,求郭靖同学得分的数学期望与方差;
,每次作答结果相互独立,且他不会主动放弃任何一次作答机会,求郭靖同学得分的数学期望与方差;
(2)在团体赛预赛中,假设A班每位参赛选手答对试题的概率均为常数 ,A班为使晋级团体赛决赛的可能性更大,应选择哪种参赛方式?请说明理由.
,A班为使晋级团体赛决赛的可能性更大,应选择哪种参赛方式?请说明理由.
 ,
, ,
, ,
, ,
, ,
,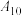 ,电脑依次出题,参赛选手按规则作答,每答对一道题得10分,答错得0分.团体赛以班级为单位,各班参赛人数必须为3的倍数,且不少于18人,团体赛分预赛和决赛两个阶段,其中预赛阶段各班可从以下两种参赛方案中任选一种参赛:
,电脑依次出题,参赛选手按规则作答,每答对一道题得10分,答错得0分.团体赛以班级为单位,各班参赛人数必须为3的倍数,且不少于18人,团体赛分预赛和决赛两个阶段,其中预赛阶段各班可从以下两种参赛方案中任选一种参赛:方案一:将班级选派的
 名参赛选手每3人一组,分成
名参赛选手每3人一组,分成 组,电脑随机分配给同一组的3名选手一道相同的试题,3人均独立答题,若这3人中至少有2人回答正确,则该小组顺利出线;若这
组,电脑随机分配给同一组的3名选手一道相同的试题,3人均独立答题,若这3人中至少有2人回答正确,则该小组顺利出线;若这 个小组都顺利出线,则该班级晋级决赛.
个小组都顺利出线,则该班级晋级决赛.方案二:将班级选派的
 名参赛选手每
名参赛选手每 人一组,分成3组,电脑随机分配给同一组的
人一组,分成3组,电脑随机分配给同一组的 名选手一道相同的试题,每人均独立答题,若这
名选手一道相同的试题,每人均独立答题,若这 个人都回答正确,则该小组顺利出线;若这3个小组中至少有2个小组顺利出线,则该班级晋级决赛.
个人都回答正确,则该小组顺利出线;若这3个小组中至少有2个小组顺利出线,则该班级晋级决赛.(1)郭靖同学参加了个人赛,已知郭靖同学答对题库中每道题的概率均为
 ,每次作答结果相互独立,且他不会主动放弃任何一次作答机会,求郭靖同学得分的数学期望与方差;
,每次作答结果相互独立,且他不会主动放弃任何一次作答机会,求郭靖同学得分的数学期望与方差;(2)在团体赛预赛中,假设A班每位参赛选手答对试题的概率均为常数
 ,A班为使晋级团体赛决赛的可能性更大,应选择哪种参赛方式?请说明理由.
,A班为使晋级团体赛决赛的可能性更大,应选择哪种参赛方式?请说明理由.
您最近一年使用:0次
名校
解题方法
5 . 某种水果按照果径大小可分为四类:标准果、优质果、精品果、礼品果.某采购商从采购的一批水果中随机抽取100个,利用水果的等级分类标准得到的数据如下:
(1)若将频率视为概率,从这100个水果中有放回地随机抽取5个,求恰好有2个水果是礼品果的概率(结果用分数表示);
(2)用样本估计总体,果园老板提出两种购销方案给采购商参考,
方案1:不分类卖出,单价为21元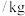 ;
;
方案2:分类卖出,分类后的水果售价如下:
从采购商的角度考虑,应该采用哪种方案?
(3)用分层抽样的方法从这100个水果中抽取10个,再从抽取的10个水果中随机抽取3个, 表示抽取的是精品果的数量,求
表示抽取的是精品果的数量,求 的分布列及方差
的分布列及方差 .
.
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
(2)用样本估计总体,果园老板提出两种购销方案给采购商参考,
方案1:不分类卖出,单价为21元
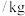 ;
;方案2:分类卖出,分类后的水果售价如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元 | 16 | 18 | 22 | 24 |
(3)用分层抽样的方法从这100个水果中抽取10个,再从抽取的10个水果中随机抽取3个,
 表示抽取的是精品果的数量,求
表示抽取的是精品果的数量,求 的分布列及方差
的分布列及方差 .
.
您最近一年使用:0次
名校
6 . 小明在石家庄市某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前55单没有奖励,超过55单的部分每单奖励12元.
(1)请分别求出甲、乙两种薪酬方案中日薪 (单位:元)与送货单数
(单位:元)与送货单数 的函数关系式;
的函数关系式;
(2)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数满足以下条件:在这100天中的派送量指标满足如图所示的直方图,其中当某天的派送量指标在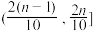
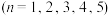 时,日平均派送量为
时,日平均派送量为 单.
单.
若将频率视为概率,回答下列问题:

①根据以上数据,设每名派送员的日薪为 (单位:元),试分别求出甲、乙两种方案的日薪
(单位:元),试分别求出甲、乙两种方案的日薪 的分布列,数学期望及方差;
的分布列,数学期望及方差;
②结合①中的数据,根据统计学的思想,帮助小明分析,他选择哪种薪酬方案比较合适,并说明你的理由.
(参考数据: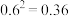 ,
, ,
, ,
,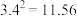 ,
,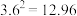 ,
,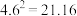 ,
,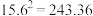 ,
, ,
,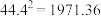 )
)
(1)请分别求出甲、乙两种薪酬方案中日薪
 (单位:元)与送货单数
(单位:元)与送货单数 的函数关系式;
的函数关系式;(2)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数满足以下条件:在这100天中的派送量指标满足如图所示的直方图,其中当某天的派送量指标在
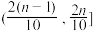
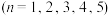 时,日平均派送量为
时,日平均派送量为 单.
单.若将频率视为概率,回答下列问题:

①根据以上数据,设每名派送员的日薪为
 (单位:元),试分别求出甲、乙两种方案的日薪
(单位:元),试分别求出甲、乙两种方案的日薪 的分布列,数学期望及方差;
的分布列,数学期望及方差;②结合①中的数据,根据统计学的思想,帮助小明分析,他选择哪种薪酬方案比较合适,并说明你的理由.
(参考数据:
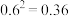 ,
, ,
, ,
,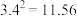 ,
,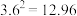 ,
,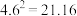 ,
,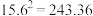 ,
, ,
,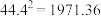 )
)
您最近一年使用:0次
2018-04-10更新
|
1071次组卷
|
3卷引用:河北省石家庄市2018届高三下学期一模考试数学(理)(A卷)试题
解题方法
7 . 高二(16)班参加青华中学红五月节目:猜歌名,班级只有一个名额,结合平时观察积累,闫某峻,贾某轩两名学生进入最后选拔,申老师为此设计了如下选拔方案:挑选8首歌进行测试,在这8首歌曲中,闫某峻能正确说出其中的6首歌名,贾某轩能正确说出每首歌名的概率均为 ,假设闫某峻、贾某轩两名学生说出每首歌名都相互独立、互不影响,现闫某峻、贾某轩从这8首歌中分别随机抽取4首进行竞猜
,假设闫某峻、贾某轩两名学生说出每首歌名都相互独立、互不影响,现闫某峻、贾某轩从这8首歌中分别随机抽取4首进行竞猜
(1)求闫某峻、贾某轩共答对3首歌名的概率;
(2)从数学期望和方差的角度分析,应选拔哪个学生代表高二(16)班参加红五月活动?
 ,假设闫某峻、贾某轩两名学生说出每首歌名都相互独立、互不影响,现闫某峻、贾某轩从这8首歌中分别随机抽取4首进行竞猜
,假设闫某峻、贾某轩两名学生说出每首歌名都相互独立、互不影响,现闫某峻、贾某轩从这8首歌中分别随机抽取4首进行竞猜(1)求闫某峻、贾某轩共答对3首歌名的概率;
(2)从数学期望和方差的角度分析,应选拔哪个学生代表高二(16)班参加红五月活动?
您最近一年使用:0次
名校
8 . 开展中小学生课后服务,是促进学生健康成长、帮助家长解决接送学生困难的重要举措 是进一步增强教育服务能力、使人民群众具有更多获得感和幸福感的民生工程. 某校为 确保学生课后服务工作顺利开展,制定了两套工作方案,为了解学生对这两个方案的支 持情况,对学生进行简单随机抽样,获得数据如表:
假设用频率估计概率,且所有学生对活动方案是否支 持相互独立.
(1)从该校支持方案一和支持方案二的学生中各随机抽取1人,设 为抽出两人中女生的个数,求
为抽出两人中女生的个数,求 的分布列与数学期望;
的分布列与数学期望;
(2)在(1)中 表示抽出两人中男生的个数,试判断方差
表示抽出两人中男生的个数,试判断方差 与
与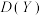 的大小.
的大小.
男 | 女 | |
支持方案一 | 24 | 16 |
支持方案二 | 25 | 35 |
(1)从该校支持方案一和支持方案二的学生中各随机抽取1人,设
 为抽出两人中女生的个数,求
为抽出两人中女生的个数,求 的分布列与数学期望;
的分布列与数学期望;(2)在(1)中
 表示抽出两人中男生的个数,试判断方差
表示抽出两人中男生的个数,试判断方差 与
与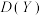 的大小.
的大小.
您最近一年使用:0次
名校
解题方法
9 . 某校设计了一个实验学科的实验考查方案;考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作,规定:至少正确完成两题便可通过,已知6道备选题中甲生有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是 ,求:
,求:
(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(2)试用统计知识分析比较两考生的实验操作能力.
 ,求:
,求:(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(2)试用统计知识分析比较两考生的实验操作能力.
您最近一年使用:0次
名校
10 . 某校举行知识竞赛,最后一个名额要在A,B两名同学中产生,测试方案如下:A,B两名学生各自从给定的4个问题中随机抽取3个问题作答,在这4个问题中,已知A能正确作答其中的3个,B能正确作答每个问题的概率都是 ,A,B两名同学作答问题相互独立.
,A,B两名同学作答问题相互独立.
(1)求A,B两名同学恰好共答对2个问题的概率;
(2)若让你投票决定参赛选手,你会选择哪名学生,简要说明理由.
 ,A,B两名同学作答问题相互独立.
,A,B两名同学作答问题相互独立.(1)求A,B两名同学恰好共答对2个问题的概率;
(2)若让你投票决定参赛选手,你会选择哪名学生,简要说明理由.
您最近一年使用:0次