1 . 已知函数 ,
, .
.
(1)讨论 的单调性;
的单调性;
(2)若 有两个零点,求实数
有两个零点,求实数 的取值范围;
的取值范围;
(3)若 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 ,
, .
.(1)讨论
 的单调性;
的单调性;(2)若
 有两个零点,求实数
有两个零点,求实数 的取值范围;
的取值范围;(3)若
 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
昨日更新
|
500次组卷
|
2卷引用:山东省菏泽第一中学八一路校区2024届高三5月月考数学试题
名校
2 . 为应对新一代小型无人机武器,某研发部门开发了甲、乙两种不同的防御武器,现对两种武器的防御效果进行测试.每次测试都是由一种武器向目标无人机发动三次攻击,每次攻击击中目标与否相互独立,每次测试都会使用性能一样的全新无人机.对于甲种武器,每次攻击击中目标无人机的概率均为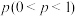 ,且击中一次目标无人机坠毁的概率为
,且击中一次目标无人机坠毁的概率为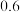 ,击中两次目标无人机必坠毁;对于乙种武器,每次攻击击中目标无人机的概率均为
,击中两次目标无人机必坠毁;对于乙种武器,每次攻击击中目标无人机的概率均为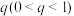 ,且击中一次目标无人机坠毁的概率为
,且击中一次目标无人机坠毁的概率为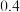 ,击中两次目标无人机坠毁的概率为
,击中两次目标无人机坠毁的概率为 ,击中三次目标无人机必坠毁.
,击中三次目标无人机必坠毁.
(1)若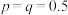 ,分别使用甲、乙两种武器进行一次测试.
,分别使用甲、乙两种武器进行一次测试.
①求甲种武器使目标无人机坠毁的概率;
②记甲、乙两种武器使目标无人机坠毁的数量为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
(2)若 ,且
,且 ,试判断在一次测试中选用甲种武器还是乙种武器使得目标无人机坠毁的概率更大?并说明理由.
,试判断在一次测试中选用甲种武器还是乙种武器使得目标无人机坠毁的概率更大?并说明理由.
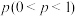 ,且击中一次目标无人机坠毁的概率为
,且击中一次目标无人机坠毁的概率为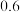 ,击中两次目标无人机必坠毁;对于乙种武器,每次攻击击中目标无人机的概率均为
,击中两次目标无人机必坠毁;对于乙种武器,每次攻击击中目标无人机的概率均为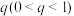 ,且击中一次目标无人机坠毁的概率为
,且击中一次目标无人机坠毁的概率为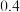 ,击中两次目标无人机坠毁的概率为
,击中两次目标无人机坠毁的概率为 ,击中三次目标无人机必坠毁.
,击中三次目标无人机必坠毁.(1)若
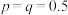 ,分别使用甲、乙两种武器进行一次测试.
,分别使用甲、乙两种武器进行一次测试.①求甲种武器使目标无人机坠毁的概率;
②记甲、乙两种武器使目标无人机坠毁的数量为
 ,求
,求 的分布列与数学期望.
的分布列与数学期望.(2)若
 ,且
,且 ,试判断在一次测试中选用甲种武器还是乙种武器使得目标无人机坠毁的概率更大?并说明理由.
,试判断在一次测试中选用甲种武器还是乙种武器使得目标无人机坠毁的概率更大?并说明理由.
您最近一年使用:0次
2024-06-10更新
|
560次组卷
|
2卷引用:山东省菏泽第一中学人民路校区2024届高三下学期5月月考数学试题
名校
3 . 已知函数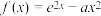 (
( 为常数),则下列结论正确的是( )
为常数),则下列结论正确的是( )
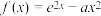 (
( 为常数),则下列结论正确的是( )
为常数),则下列结论正确的是( )A.当 时, 时, 在 在 处的切线方程为 处的切线方程为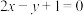 |
B.若 有3个零点,则 有3个零点,则 的取值范围为 的取值范围为 |
C.当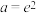 时, 时, 是 是 的极大值点 的极大值点 |
D.当 时, 时, 有唯一零点 有唯一零点 ,且 ,且 |
您最近一年使用:0次
2024-06-08更新
|
665次组卷
|
3卷引用:山东省菏泽市定陶区第一中学2023-2024学年高二下学期5月月考数学试题
名校
解题方法
4 . 已知PC是三棱锥 外接球的直径,且
外接球的直径,且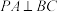 ,
,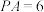 ,三棱锥
,三棱锥 体积的最大值为8,则其外接球的表面积为
体积的最大值为8,则其外接球的表面积为______ .
 外接球的直径,且
外接球的直径,且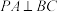 ,
,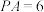 ,三棱锥
,三棱锥 体积的最大值为8,则其外接球的表面积为
体积的最大值为8,则其外接球的表面积为
您最近一年使用:0次
2024-06-04更新
|
780次组卷
|
3卷引用:山东省菏泽市第一中学八一路校区2023-2024学年高一下学期第三次月考数学试题
5 . 我们知道,在平面内取定单位正交基底建立坐标系后,任意一个平面向量,都可以用二元有序实数对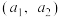 表示.平面向量又称为二维向量.一般地,n元有序实数组
表示.平面向量又称为二维向量.一般地,n元有序实数组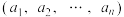 称为n维向量,它是二维向量的推广.类似二维向量,对于n维向量,也可定义两个向量的数量积、向量的长度(模)等:设
称为n维向量,它是二维向量的推广.类似二维向量,对于n维向量,也可定义两个向量的数量积、向量的长度(模)等:设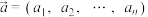 ,
,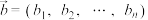 ,则
,则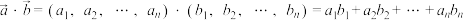 ;
;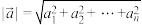 .已知向量
.已知向量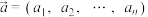 满足
满足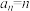 ,向量
,向量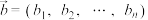 满足
满足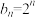 .
.
(1)求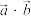 的值;
的值;
(2)若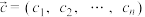 ,其中
,其中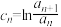 ,当
,当 且
且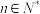 时,证明:
时,证明: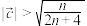 .
.
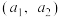 表示.平面向量又称为二维向量.一般地,n元有序实数组
表示.平面向量又称为二维向量.一般地,n元有序实数组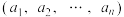 称为n维向量,它是二维向量的推广.类似二维向量,对于n维向量,也可定义两个向量的数量积、向量的长度(模)等:设
称为n维向量,它是二维向量的推广.类似二维向量,对于n维向量,也可定义两个向量的数量积、向量的长度(模)等:设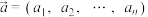 ,
,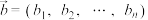 ,则
,则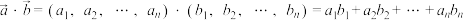 ;
;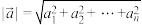 .已知向量
.已知向量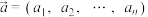 满足
满足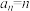 ,向量
,向量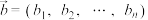 满足
满足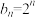 .
.(1)求
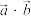 的值;
的值;(2)若
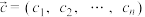 ,其中
,其中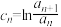 ,当
,当 且
且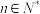 时,证明:
时,证明: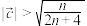 .
.
您最近一年使用:0次
名校
解题方法
6 . 若 ,关于
,关于 的不等式
的不等式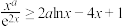 恒成立,则正实数
恒成立,则正实数 的最大值为
的最大值为______ .
 ,关于
,关于 的不等式
的不等式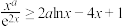 恒成立,则正实数
恒成立,则正实数 的最大值为
的最大值为
您最近一年使用:0次
2024-05-30更新
|
1344次组卷
|
3卷引用:山东省菏泽市定陶区第一中学2023-2024学年高二下学期5月月考数学试题
山东省菏泽市定陶区第一中学2023-2024学年高二下学期5月月考数学试题广东省广州市华南师范大学附属中学2024届高三下学期高考适应性练习(4月)数学试题(已下线)第3题 妙解指对函数最值(压轴小题)
7 . 定义:若曲线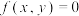 或函数
或函数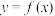 的图象上的两个不同点处的切线互相重合,则称该切线为曲线
的图象上的两个不同点处的切线互相重合,则称该切线为曲线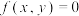 或函数
或函数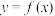 的图象的“自公切线”.
的图象的“自公切线”.
(1)设曲线C: ,在直角坐标系中作出曲线C的图象,并判断C是否存在“自公切线”?(给出结论即可,不必说明理由)
,在直角坐标系中作出曲线C的图象,并判断C是否存在“自公切线”?(给出结论即可,不必说明理由) 时,函数
时,函数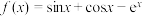 不存在“自公切线”;
不存在“自公切线”;
(3)证明:当 ,
,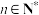 时,
时,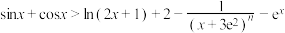 .
.
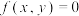 或函数
或函数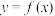 的图象上的两个不同点处的切线互相重合,则称该切线为曲线
的图象上的两个不同点处的切线互相重合,则称该切线为曲线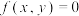 或函数
或函数 的图象的“自公切线”.
的图象的“自公切线”.(1)设曲线C:
 ,在直角坐标系中作出曲线C的图象,并判断C是否存在“自公切线”?(给出结论即可,不必说明理由)
,在直角坐标系中作出曲线C的图象,并判断C是否存在“自公切线”?(给出结论即可,不必说明理由)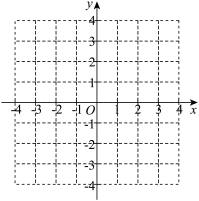
 时,函数
时,函数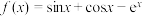 不存在“自公切线”;
不存在“自公切线”;(3)证明:当
 ,
,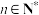 时,
时,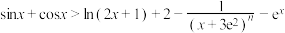 .
.
您最近一年使用:0次
2024-05-30更新
|
427次组卷
|
2卷引用:山东省菏泽市定陶区第一中学2023-2024学年高二下学期5月月考数学试题
名校
解题方法
8 . 已知抛物线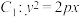 的焦点
的焦点 与圆
与圆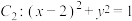 的圆心重合,若点
的圆心重合,若点 、
、 分别在
分别在 、
、 上运动,点
上运动,点 则下列说法正确的是( )
则下列说法正确的是( )
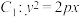 的焦点
的焦点 与圆
与圆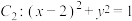 的圆心重合,若点
的圆心重合,若点 、
、 分别在
分别在 、
、 上运动,点
上运动,点 则下列说法正确的是( )
则下列说法正确的是( )A.当直线 经过 经过 时, 时, |
B.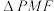 的周长最小值为 的周长最小值为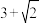 |
C.过 作圆 作圆 的切线,切点分别为 的切线,切点分别为 ,则当四边形 ,则当四边形 的面积最小时, 的面积最小时, |
D.设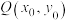 ,则 ,则 的最大值为 的最大值为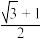 |
您最近一年使用:0次
名校
解题方法
9 . 已知函数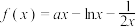 .
.
(1)当 时,求
时,求 的极值;
的极值;
(2)当 时,不等式
时,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(3)证明: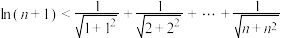 .
.
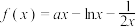 .
.(1)当
 时,求
时,求 的极值;
的极值;(2)当
 时,不等式
时,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围;(3)证明:
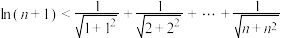 .
.
您最近一年使用:0次
名校
10 . 在四面体 中,
中,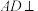 平面
平面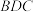 ,
, ,若
,若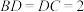 ,
,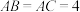 ,则四面体
,则四面体 外接球的半径为( )
外接球的半径为( )
 中,
中,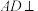 平面
平面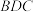 ,
, ,若
,若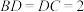 ,
,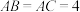 ,则四面体
,则四面体 外接球的半径为( )
外接球的半径为( )A. | B. | C.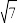 | D. |
您最近一年使用:0次



