1 . 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,点O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接DF,连接OF交AD于点G.
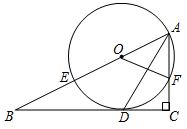
(1)求证:BC是⊙O的切线;
(2)设AB=a,AF=b,试用含a,b的代数式表示线段AD的长;
(3)若BE=5,sinB=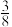 ,求DG的长.
,求DG的长.

(1)求证:BC是⊙O的切线;
(2)设AB=a,AF=b,试用含a,b的代数式表示线段AD的长;
(3)若BE=5,sinB=
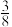 ,求DG的长.
,求DG的长.
您最近一年使用:0次
2 . 已知数列 的前
的前 项和为
项和为 ,满足
,满足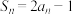 ,
, ,数列
,数列 满足
满足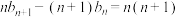 ,
, ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求证:数列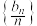 是等差数列,求数列
是等差数列,求数列 的通项公式;
的通项公式;
(3)若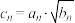 ,数列
,数列 的前
的前 项和为
项和为 ,对任意的
,对任意的 ,都有
,都有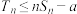 ,求实数
,求实数 的取值范围.
的取值范围.
 的前
的前 项和为
项和为 ,满足
,满足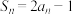 ,
, ,数列
,数列 满足
满足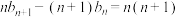 ,
, ,且
,且 .
.(1)求数列
 的通项公式;
的通项公式;(2)求证:数列
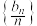 是等差数列,求数列
是等差数列,求数列 的通项公式;
的通项公式;(3)若
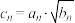 ,数列
,数列 的前
的前 项和为
项和为 ,对任意的
,对任意的 ,都有
,都有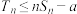 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2020-09-03更新
|
662次组卷
|
2卷引用:黑龙江省哈尔滨师范大学青冈实验中学校2019-2020学年高二上学期开学考试(8月)数学试题
3 . 在平面直角坐标系中,四边形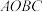 是矩形,点
是矩形,点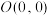 ,点
,点 ,点
,点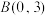 .以点
.以点 为中心,顺时针旋转矩形
为中心,顺时针旋转矩形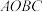 ,得到矩形
,得到矩形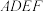 ,点
,点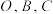 的对应点分别为
的对应点分别为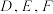 .
.
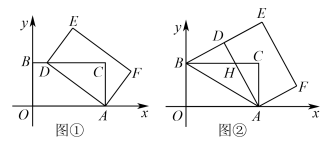
(1)如图①,当点 落在
落在 边上时,求点
边上时,求点 的坐标;
的坐标;
(2)如图②,当点 落在线段
落在线段 上时,
上时, 与
与 交于点
交于点 .
.
①求证 ;②求点
;②求点 的坐标.
的坐标.
(3)记 为矩形
为矩形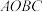 对角线的交点,
对角线的交点, 为
为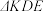 的面积,求
的面积,求 的取值范围(直接写出结果即可).
的取值范围(直接写出结果即可).
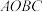 是矩形,点
是矩形,点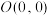 ,点
,点 ,点
,点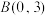 .以点
.以点 为中心,顺时针旋转矩形
为中心,顺时针旋转矩形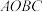 ,得到矩形
,得到矩形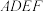 ,点
,点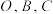 的对应点分别为
的对应点分别为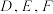 .
.
(1)如图①,当点
 落在
落在 边上时,求点
边上时,求点 的坐标;
的坐标;(2)如图②,当点
 落在线段
落在线段 上时,
上时, 与
与 交于点
交于点 .
.①求证
 ;②求点
;②求点 的坐标.
的坐标.(3)记
 为矩形
为矩形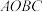 对角线的交点,
对角线的交点, 为
为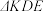 的面积,求
的面积,求 的取值范围(直接写出结果即可).
的取值范围(直接写出结果即可).
您最近一年使用:0次
名校
解题方法
4 . 已知椭圆E: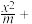 y2=1(m>1)的离心率为
y2=1(m>1)的离心率为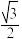 ,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.
,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.
(Ⅰ)求m的值;
(Ⅱ)求证:直线A0B恒过定点.
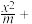 y2=1(m>1)的离心率为
y2=1(m>1)的离心率为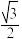 ,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.
,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.(Ⅰ)求m的值;
(Ⅱ)求证:直线A0B恒过定点.
您最近一年使用:0次
5 . 如图,四棱锥 中,
中,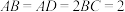 ,
, ,
, ,
, 为正三角形.若
为正三角形.若 ,且
,且 与底面
与底面 所成角的正切值为
所成角的正切值为 .
.
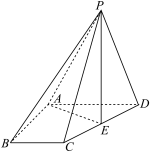
(1)证明:平面 平面
平面 ;
;
(2) 是线段
是线段 上一点,记
上一点,记 ,是否存在实数
,是否存在实数 ,使二面角
,使二面角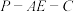 的余弦值为
的余弦值为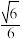 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 中,
中,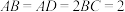 ,
, ,
, ,
, 为正三角形.若
为正三角形.若 ,且
,且 与底面
与底面 所成角的正切值为
所成角的正切值为 .
.
(1)证明:平面
 平面
平面 ;
;(2)
 是线段
是线段 上一点,记
上一点,记 ,是否存在实数
,是否存在实数 ,使二面角
,使二面角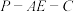 的余弦值为
的余弦值为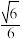 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2020-03-22更新
|
977次组卷
|
3卷引用:江西省南昌市2017-2018学年度高三第二轮复习测试卷理科数学(七)
名校
6 . 已知函数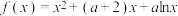 .
.
(1)讨论函数 的单调区间;
的单调区间;
(2)若存在两个不相等的正数 ,
, ,满足
,满足 ,证明:
,证明: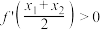 .
.
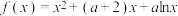 .
.(1)讨论函数
 的单调区间;
的单调区间;(2)若存在两个不相等的正数
 ,
, ,满足
,满足 ,证明:
,证明: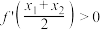 .
.
您最近一年使用:0次
21-22高二·湖南·课后作业
名校
7 . 在正方体 中,E,F分别是
中,E,F分别是 ,CD的中点.求证:平面
,CD的中点.求证:平面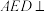 平面
平面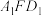 .
.
 中,E,F分别是
中,E,F分别是 ,CD的中点.求证:平面
,CD的中点.求证:平面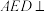 平面
平面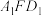 .
.
您最近一年使用:0次
2019-10-10更新
|
127次组卷
|
6卷引用:第二章 第三节 2.3直线、平面垂直的判定及其性质
8 . 如图1,在梯形 中,
中, ,
, ,
, 为
为 中点,
中点, 是
是 与
与 的交点,将
的交点,将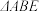 沿
沿 翻折到图2中
翻折到图2中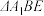 的位置得到四棱锥
的位置得到四棱锥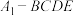 .
.
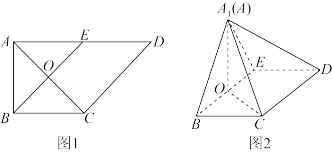
(1)求证: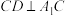
(2)若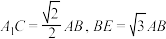 ,求二面角
,求二面角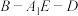 的余弦值.
的余弦值.
 中,
中, ,
, ,
, 为
为 中点,
中点, 是
是 与
与 的交点,将
的交点,将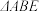 沿
沿 翻折到图2中
翻折到图2中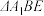 的位置得到四棱锥
的位置得到四棱锥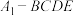 .
.
(1)求证:
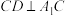
(2)若
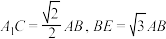 ,求二面角
,求二面角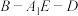 的余弦值.
的余弦值.
您最近一年使用:0次
2019-10-12更新
|
1845次组卷
|
7卷引用:安徽省六安市第一中学2019-2020学年高二下学期3月开学考试数学(理)试题
名校
9 . 如图,在四棱锥 中,平面
中,平面 平面ABCD,
平面ABCD,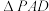 是等边三角形,四边形ABCD是矩形,
是等边三角形,四边形ABCD是矩形,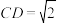 ,F为棱PA上一点,且
,F为棱PA上一点,且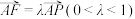 ,M为AD的中点,四棱锥
,M为AD的中点,四棱锥 的体积为
的体积为 .
.

(1)若 ,N是PB的中点,求证:平面
,N是PB的中点,求证:平面 平面PCD;
平面PCD;
(2)是否存在 ,使得平面FMB与平面PAD所成的二面角余弦的绝对值为
,使得平面FMB与平面PAD所成的二面角余弦的绝对值为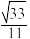 .
.
 中,平面
中,平面 平面ABCD,
平面ABCD,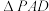 是等边三角形,四边形ABCD是矩形,
是等边三角形,四边形ABCD是矩形,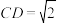 ,F为棱PA上一点,且
,F为棱PA上一点,且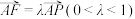 ,M为AD的中点,四棱锥
,M为AD的中点,四棱锥 的体积为
的体积为 .
.
(1)若
 ,N是PB的中点,求证:平面
,N是PB的中点,求证:平面 平面PCD;
平面PCD;(2)是否存在
 ,使得平面FMB与平面PAD所成的二面角余弦的绝对值为
,使得平面FMB与平面PAD所成的二面角余弦的绝对值为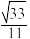 .
.
您最近一年使用:0次
2019-10-21更新
|
2277次组卷
|
3卷引用:四川省成都市石室中学2019-2020学年高三上学期入学考数学(理)试题
四川省成都市石室中学2019-2020学年高三上学期入学考数学(理)试题(已下线)四川省成都市石室中学2020-2021学年高三下学期开学考试模拟(一)(理科)试题河北省邯郸市曲周县第一中学2020-2021学年高二下学期3月月考数学试题
名校
解题方法
10 . 已知函数 .
.
(1)若关于x的不等式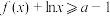 对任意的正数x恒成立,求实数a的取值范围.
对任意的正数x恒成立,求实数a的取值范围.
(2)证明: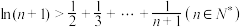 .
.
 .
.(1)若关于x的不等式
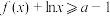 对任意的正数x恒成立,求实数a的取值范围.
对任意的正数x恒成立,求实数a的取值范围.(2)证明:
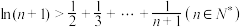 .
.
您最近一年使用:0次
2020-09-26更新
|
191次组卷
|
2卷引用:安徽省阜阳市太和第一中学2020-2021学年高三上学期开学摸底检测数学(文)试题



