解题方法
1 . 已知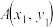 ,
, 是椭圆T.
是椭圆T.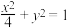 上的两点,且A点位于第一象限.过A作x轴的垂线,垂足为点C,点D满足
上的两点,且A点位于第一象限.过A作x轴的垂线,垂足为点C,点D满足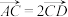 ,延长
,延长 交T于点
交T于点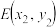 .
.
(1)设直线 ,
, 的斜率分别为
的斜率分别为 ,
, .
.
(i)求证: ;
;
(ii)证明: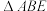 是直角三角形;
是直角三角形;
(2)求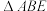 的面积的最大值.
的面积的最大值.
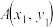 ,
, 是椭圆T.
是椭圆T.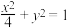 上的两点,且A点位于第一象限.过A作x轴的垂线,垂足为点C,点D满足
上的两点,且A点位于第一象限.过A作x轴的垂线,垂足为点C,点D满足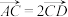 ,延长
,延长 交T于点
交T于点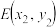 .
.(1)设直线
 ,
, 的斜率分别为
的斜率分别为 ,
, .
.(i)求证:
 ;
;(ii)证明:
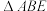 是直角三角形;
是直角三角形;(2)求
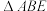 的面积的最大值.
的面积的最大值.
您最近一年使用:0次
2020·全国·模拟预测
2 . 如图,已知 是抛物线
是抛物线 上的任意一点,
上的任意一点,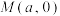 ,
,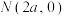 ,
,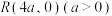 ,连接
,连接 并延长交抛物线于另一点
并延长交抛物线于另一点 ,连接
,连接 并延长交抛物线于另一点
并延长交抛物线于另一点 ,连接
,连接 并延长交抛物线于另一点
并延长交抛物线于另一点 ,设直线
,设直线 与
与 的交点为
的交点为 .
.

(1)求证:直线 过点
过点 ;
;
(2)设 和四边形
和四边形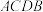 的面积分别为
的面积分别为 ,
, ,当
,当 变化时,
变化时, 是否为定值?若是,求出此定值,并说明理由;若不是,求出
是否为定值?若是,求出此定值,并说明理由;若不是,求出 关于
关于 的表达式.
的表达式.
 是抛物线
是抛物线 上的任意一点,
上的任意一点,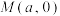 ,
,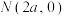 ,
,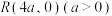 ,连接
,连接 并延长交抛物线于另一点
并延长交抛物线于另一点 ,连接
,连接 并延长交抛物线于另一点
并延长交抛物线于另一点 ,连接
,连接 并延长交抛物线于另一点
并延长交抛物线于另一点 ,设直线
,设直线 与
与 的交点为
的交点为 .
.
(1)求证:直线
 过点
过点 ;
;(2)设
 和四边形
和四边形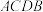 的面积分别为
的面积分别为 ,
, ,当
,当 变化时,
变化时, 是否为定值?若是,求出此定值,并说明理由;若不是,求出
是否为定值?若是,求出此定值,并说明理由;若不是,求出 关于
关于 的表达式.
的表达式.
您最近一年使用:0次
名校
解题方法
3 . 已知数列 是等比数列,
是等比数列, ,且
,且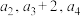 成等差数列.数列
成等差数列.数列 满足:
满足: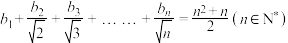 .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)求证: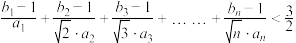 .
.
 是等比数列,
是等比数列, ,且
,且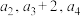 成等差数列.数列
成等差数列.数列 满足:
满足: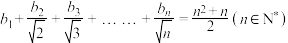 .
.(1)求数列
 和
和 的通项公式;
的通项公式;(2)求证:
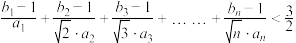 .
.
您最近一年使用:0次
2020-12-01更新
|
911次组卷
|
4卷引用:2020届浙江省绍兴市高三下学期4月第一次高考模拟考试数学试题
2020届浙江省绍兴市高三下学期4月第一次高考模拟考试数学试题(已下线)专题09 数列与数学归纳法-2021年浙江省高考数学命题规律大揭秘【学科网名师堂】(已下线)专题20 数列综合-2020年高考数学母题题源全揭秘(浙江专版)山东省德州市第一中学2023-2024学年高二下学期3月月考数学试题
4 . 设数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
,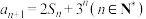 .
.
(1)求 (用
(用 表示);
表示);
(2)求证:当 时,不等式
时,不等式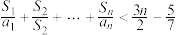 成立.
成立.
 的前
的前 项和为
项和为 ,且满足
,且满足 ,
,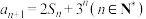 .
.(1)求
 (用
(用 表示);
表示);(2)求证:当
 时,不等式
时,不等式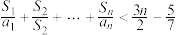 成立.
成立.
您最近一年使用:0次
5 . 设函数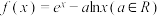 .
.
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)当 时,求证:
时,求证: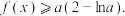
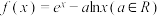 .
.(1)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(2)当
 时,求证:
时,求证: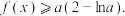
您最近一年使用:0次
2020-09-21更新
|
375次组卷
|
3卷引用:【省级联考】山西省2019届高三考前适应性训练二(二模)文科数学试题
解题方法
6 . 已知椭圆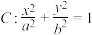 的左、右焦点分别为
的左、右焦点分别为 ,
, ,且
,且 ,
,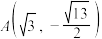 是椭圆上一点.
是椭圆上一点.
(1)求椭圆方程的离心率
(2)若 为椭圆
为椭圆 上异于顶点的任意一点,
上异于顶点的任意一点, ,
, 分别为椭圆的右顶点和上顶点.直线
分别为椭圆的右顶点和上顶点.直线 与
与 轴交于点
轴交于点 ,直线
,直线 与
与 轴交于点
轴交于点 ,求证:
,求证: 为定值.
为定值.
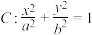 的左、右焦点分别为
的左、右焦点分别为 ,
, ,且
,且 ,
,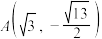 是椭圆上一点.
是椭圆上一点.(1)求椭圆方程的离心率
(2)若
 为椭圆
为椭圆 上异于顶点的任意一点,
上异于顶点的任意一点, ,
, 分别为椭圆的右顶点和上顶点.直线
分别为椭圆的右顶点和上顶点.直线 与
与 轴交于点
轴交于点 ,直线
,直线 与
与 轴交于点
轴交于点 ,求证:
,求证: 为定值.
为定值.
您最近一年使用:0次
7 . 已知函数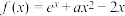 .
.
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)若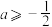 时,求证:对任意的
时,求证:对任意的 ,有
,有 .
.
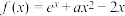 .
.(1)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(2)若
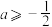 时,求证:对任意的
时,求证:对任意的 ,有
,有 .
.
您最近一年使用:0次
解题方法
8 . 已知函数 ,
,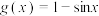 .
.
(1)求 在点
在点 处的切线;
处的切线;
(2)研究函数 的单调性,并求出
的单调性,并求出 极值;
极值;
(3)求证: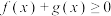 .
.
 ,
,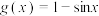 .
.(1)求
 在点
在点 处的切线;
处的切线;(2)研究函数
 的单调性,并求出
的单调性,并求出 极值;
极值;(3)求证:
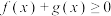 .
.
您最近一年使用:0次
解题方法
9 . 已知椭圆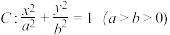 的长轴长是短轴长的2倍,A,B分别为椭圆的左顶点和下顶点,且
的长轴长是短轴长的2倍,A,B分别为椭圆的左顶点和下顶点,且 的面积为1.
的面积为1.
(1)求椭圆C的方程;
(2)设点M为椭圆上位于第一象限内一动点,直线 与
与 轴交于点C,直线
轴交于点C,直线 与
与 轴交于点D,求证:四边形
轴交于点D,求证:四边形 的面积为定值.
的面积为定值.
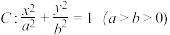 的长轴长是短轴长的2倍,A,B分别为椭圆的左顶点和下顶点,且
的长轴长是短轴长的2倍,A,B分别为椭圆的左顶点和下顶点,且 的面积为1.
的面积为1.(1)求椭圆C的方程;
(2)设点M为椭圆上位于第一象限内一动点,直线
 与
与 轴交于点C,直线
轴交于点C,直线 与
与 轴交于点D,求证:四边形
轴交于点D,求证:四边形 的面积为定值.
的面积为定值.
您最近一年使用:0次
2020-03-16更新
|
259次组卷
|
2卷引用:2020届湖北省宜昌市第二中学高三上学期10月月考数学(文)试题
解题方法
10 . 如图,已知椭圆 经过点
经过点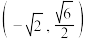 ,且离心率
,且离心率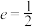 ,过右焦点
,过右焦点 且不与坐标轴垂直的直线
且不与坐标轴垂直的直线 与椭圆
与椭圆 相交于
相交于 两点.
两点.
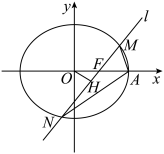
(1)求椭圆 的标准方程;
的标准方程;
(2)设椭圆 的右顶点为
的右顶点为 ,线段
,线段 的中点为
的中点为 ,记直线
,记直线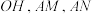 的斜率分别为
的斜率分别为 ,求证:
,求证: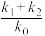 为定值.
为定值.
 经过点
经过点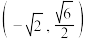 ,且离心率
,且离心率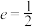 ,过右焦点
,过右焦点 且不与坐标轴垂直的直线
且不与坐标轴垂直的直线 与椭圆
与椭圆 相交于
相交于 两点.
两点.
(1)求椭圆
 的标准方程;
的标准方程;(2)设椭圆
 的右顶点为
的右顶点为 ,线段
,线段 的中点为
的中点为 ,记直线
,记直线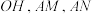 的斜率分别为
的斜率分别为 ,求证:
,求证: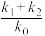 为定值.
为定值.
您最近一年使用:0次



