真题
1 . 已知 ,数列
,数列 满足
满足 .
.
(1)已知数列 极限存在且大于零,求
极限存在且大于零,求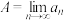 (将A用a表示);
(将A用a表示);
(2)设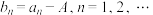 ,证明:
,证明: ;
;
(3)若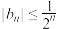 对
对 都成立,求a的取值范围.
都成立,求a的取值范围.
 ,数列
,数列 满足
满足 .
.(1)已知数列
 极限存在且大于零,求
极限存在且大于零,求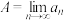 (将A用a表示);
(将A用a表示);(2)设
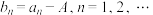 ,证明:
,证明: ;
;(3)若
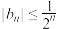 对
对 都成立,求a的取值范围.
都成立,求a的取值范围.
您最近一年使用:0次
真题
解题方法
2 . 如图,某地为了开发旅游资源,欲修建一条连接风景点P和居民区O的公路,点P所在的山坡面与山脚所在水平面 所成的二面角为
所成的二面角为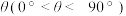 ,且
,且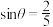 ,点P到平面
,点P到平面 的距离
的距离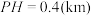 .沿山脚原有一段笔直的公路AB可供利用,从点O到山脚修路的造价为a万元
.沿山脚原有一段笔直的公路AB可供利用,从点O到山脚修路的造价为a万元 ,原有公路改建费用为
,原有公路改建费用为 万元
万元 ,当山坡上公路长度为
,当山坡上公路长度为 时,其造价为
时,其造价为 万元,已知
万元,已知 ,
, ,
,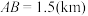 ,
,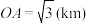 .
.

(1)在AB上求一点D,使沿折线PDAO修建公路的总造价最小;
(2)对于(1)中得到的点D,在DA上求一点E,使沿折线PDEO修建公路的总造价最小;
(3)在AB上是否存在两个不同的点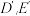 ,使沿折线
,使沿折线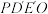 修建公路的总造价小于(2)中得到的最小总造价,证明你的结论.
修建公路的总造价小于(2)中得到的最小总造价,证明你的结论.
 所成的二面角为
所成的二面角为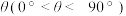 ,且
,且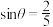 ,点P到平面
,点P到平面 的距离
的距离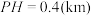 .沿山脚原有一段笔直的公路AB可供利用,从点O到山脚修路的造价为a万元
.沿山脚原有一段笔直的公路AB可供利用,从点O到山脚修路的造价为a万元 ,原有公路改建费用为
,原有公路改建费用为 万元
万元 ,当山坡上公路长度为
,当山坡上公路长度为 时,其造价为
时,其造价为 万元,已知
万元,已知 ,
, ,
,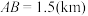 ,
,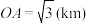 .
.
(1)在AB上求一点D,使沿折线PDAO修建公路的总造价最小;
(2)对于(1)中得到的点D,在DA上求一点E,使沿折线PDEO修建公路的总造价最小;
(3)在AB上是否存在两个不同的点
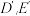 ,使沿折线
,使沿折线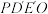 修建公路的总造价小于(2)中得到的最小总造价,证明你的结论.
修建公路的总造价小于(2)中得到的最小总造价,证明你的结论.
您最近一年使用:0次
真题
3 . 是否存在常数 使得等式
使得等式 对一切自然数n都成立?并证明你的结论.
对一切自然数n都成立?并证明你的结论.
 使得等式
使得等式 对一切自然数n都成立?并证明你的结论.
对一切自然数n都成立?并证明你的结论.
您最近一年使用:0次
2022-11-09更新
|
200次组卷
|
8卷引用:1989年普通高等学校招生考试数学(理)试题(全国卷)
4 . 已知函数
(Ⅰ)若 ,试确定函数
,试确定函数 的单调区间;
的单调区间;
(Ⅱ)若 ,且对于任意
,且对于任意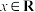 ,
,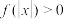 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
(Ⅲ)设函数 ,求证:
,求证: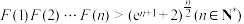 .
.

(Ⅰ)若
 ,试确定函数
,试确定函数 的单调区间;
的单调区间;(Ⅱ)若
 ,且对于任意
,且对于任意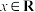 ,
,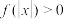 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;(Ⅲ)设函数
 ,求证:
,求证: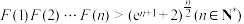 .
.
您最近一年使用:0次
2019-01-30更新
|
2547次组卷
|
13卷引用:2007年普通高等学校招生全国统一考试理科数学卷(福建)
2007年普通高等学校招生全国统一考试理科数学卷(福建)2007年普通高等学校招生考试数学(理)试题(福建卷)(已下线)2011-2012学年湖北省仙桃市高二下学期期中考试理科数学试卷(已下线)2012-2013学年湖北武汉部分重点中学高二下学期期中考试理数学试卷(已下线)2013届山东省临沂十八中高三第二次(3月)周测理科数学试卷2015届北京市西城区实验学校高三1月月考理科数学试卷2014-2015学年河北省唐山市一中高二下学期期中考试理科数学试卷2014-2015学年山东省曲阜师大附中高二下学期期中考试理科数学试卷2019届百师联盟全国高三冲刺考(四)全国 II 卷理科数学试卷陕西省西安交通大学附属中学2019-2020学年高二下学期5月月考理科数学试题天津市红桥区2022届高三下学期二模数学试题福建省德化第一中学2021-2022学年高二下学期第二次质检数学试题四川省德阳市第五中学2022-2023学年高二下学期3月月考数学(理)试题
真题
5 . 设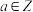 ,已知定义在R上的函数
,已知定义在R上的函数 在区间
在区间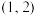 内有一个零点
内有一个零点 ,
, 为
为 的导函数.
的导函数.
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)设 ,函数
,函数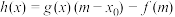 ,求证:
,求证: ;
;
(Ⅲ)求证:存在大于0的常数 ,使得对于任意的正整数
,使得对于任意的正整数 ,且
,且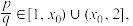 满足
满足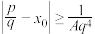 .
.
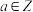 ,已知定义在R上的函数
,已知定义在R上的函数 在区间
在区间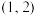 内有一个零点
内有一个零点 ,
, 为
为 的导函数.
的导函数.(Ⅰ)求
 的单调区间;
的单调区间;(Ⅱ)设
 ,函数
,函数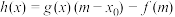 ,求证:
,求证: ;
;(Ⅲ)求证:存在大于0的常数
 ,使得对于任意的正整数
,使得对于任意的正整数 ,且
,且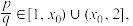 满足
满足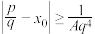 .
.
您最近一年使用:0次
2017-08-07更新
|
6075次组卷
|
12卷引用:2017年全国普通高等学校招生统一考试理科数学(天津卷精编版)
2017年全国普通高等学校招生统一考试理科数学(天津卷精编版)(已下线)2019高考备考一轮复习精品资料 【理】专题十一 函数与方程 教学案(已下线)2019高考热点题型和提分秘籍 【理数】专题11 导数的应用 (教学案)(已下线)2019高考热点题型和提分秘籍 【文数】专题11 导数的应用 (教学案)(已下线)2019高考热点题型和提分秘籍 【理数】专题10 导数的概念及运算 (教学案)(已下线)专题19 函数与导数综合-五年(2016-2020)高考数学(理)真题分项(二)(已下线)考点07 导数与函数的单调性、极值与最值-备战2022年高考数学(理)一轮复习考点微专题(已下线)专题12 导数-五年(2017-2021)高考数学真题分项(新高考地区专用)(已下线)专题03 导数及其应用-五年(2017-2021)高考数学真题分项汇编(文科+理科)(已下线)重组卷05(已下线)专题22 导数解答题(理科)-3专题13导数及其应用(第二部分)
真题
名校
6 . 已知函数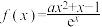 .
.
(1)求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)证明:当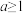 时,
时,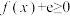 .
.
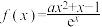 .
.(1)求曲线
 在点
在点 处的切线方程;
处的切线方程;(2)证明:当
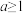 时,
时,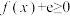 .
.
您最近一年使用:0次
2018-06-09更新
|
26858次组卷
|
49卷引用:2018年全国普通高等学校招生统一考试文科数学(新课标III卷)
2018年全国普通高等学校招生统一考试文科数学(新课标III卷)(已下线)2018年高考题及模拟题汇编 【文科】2.函数与导数福建省永春县第一中学2017-2018高二下学期期末考试数学(文)试题(已下线)2019年一轮复习讲练测【新课标版文】3.2导数在研究函数中的应用【讲】广西南宁市第八中学2017-2018学年高二下学期期末考试数学(文)试题【校级联考】江西省南昌市第八中学、第二十三中学、第十三中学2019届高三第一学期期中联考文科数学试题黑龙江省大庆市第四中学2018-2019学年高二下学期第二次月考数学(文)试题安徽省六安市第一中学2019-2020学年高二下学期第一次在线自测数学(文)试题安徽省蚌埠二中2019-2020学年高二下学期开学检测文科数学试题山西省晋中市和诚中学2019-2020学年高三下学期1月月考数学(理)试题湖北省武汉市钢城第四中学2019-2020学年高二下学期期中数学试题河南省南阳市2019-2020学年高二下学期期中质量评估数学(理)试题四川省南充市南部县盘龙中学2019-2020学年高二下学期期中考试数学试题(已下线)专题21 函数与导数综合-2020年高考数学(理)母题题源解密(全国Ⅲ专版)(已下线)专题04 导数及其应用(解答题)——三年(2018-2020)高考真题文科数学分项汇编(已下线)专题09 导数的综合应用-十年(2011-2020)高考真题数学分项(已下线)专题20 函数与导数综合-2020年高考数学(文)母题题源解密(全国Ⅲ专版)(已下线)专题13 函数与导数综合-五年(2016-2020)高考数学(文)真题分项广西兴安县第三中学2021届高三10月月考数学试题辽宁省沈阳市郊联体2020-2021学年高三上学期期中考试试题宁夏石嘴山市平罗中学2021届高三(上)期中数学(文科)试题宁夏平罗中学2021届高三上学期期中考试数学(文)试题湖南省常德市淮阳中学2020-2021学年高二上学期期末数学试题(已下线)专题04 利用导数证明不等式 第一篇 热点、难点突破篇(讲)- 2021年高考二轮复习讲练测(浙江专用)(已下线)专题4.6 导数-2021年高考数学解答题挑战满分专项训练(新高考地区专用)(已下线)专题03 导数及其应用-备战2021年高考数学(文)纠错笔记(已下线)押第5题 导数的几何意义-备战2021年高考数学(文)临考题号押题(全国卷1)四川省宜宾市天立学校2021届高三下学期模拟数学(文)试题(已下线)解密05 导数及其应用(分层训练)-【高频考点解密】2021年高考数学(文)二轮复习讲义+分层训练(已下线)专题04 函数导数及其应用-十年(2012-2021)高考数学真题分项汇编(全国通用)(已下线)专题03 导数及其应用-五年(2017-2021)高考数学真题分项汇编(文科+理科)(已下线)第十二课时 课后 第五章章末复习课陕西省西安市长安区第一中学2021-2022学年高二上学期期中文科数学试题(已下线)专题04 利用导数证明不等式(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》(已下线)专题25 导数(文科)解答题20题-备战2022年高考数学冲刺横向强化精练精讲新疆乌苏市第一中学2021-2022学年高二3月月考数学(文)试题(已下线)专题04 导数解答题-2四川省南充市南部县南部中学2022-2023学年高三上学期第一次月考(文科)月考数学试题四川省内江市威远县威远中学校2022-2023学年高三上学期期中数学(文)试题宁夏石嘴山市平罗中学2023届高三(重点班)上学期期中考试数学(文)试题陕西省汉中市龙岗学校2022-2023学年高二上学期期末理科数学试题甘肃省定西市英才高级中学2022-2023学年高三上学期期末数学试题(已下线)第二篇 函数与导数专题4 不等式 微点9 泰勒展开式(已下线)2.6 导数及其应用(不等式、函数零点)(高考真题素材之十年高考)(已下线)2.6 导数及其应用(极值问题、最值问题)(高考真题素材之十年高考)(已下线)专题22 导数解答题(文科)-2专题36导数及其应用解答题(第二部分)(已下线)第八章 利用导数证明不等式 专题四 单变量含参不等式证法之合理消参 微点1 单变量含参不等式证法之合理消参(一)四川省广安市育才学校2023-2024学年高二下学期期中考试数学试题
真题
解题方法
7 . 已知集合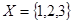 ,
,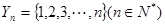 ,
,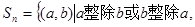
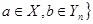 ,令
,令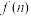 表示集合
表示集合 所含元素的个数.
所含元素的个数.
(1)写出 的值;
的值;
(2)当 时,写出
时,写出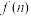 的表达式,并用数学归纳法证明.
的表达式,并用数学归纳法证明.
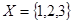 ,
,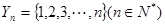 ,
,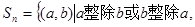
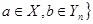 ,令
,令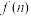 表示集合
表示集合 所含元素的个数.
所含元素的个数.(1)写出
 的值;
的值;(2)当
 时,写出
时,写出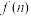 的表达式,并用数学归纳法证明.
的表达式,并用数学归纳法证明.
您最近一年使用:0次
2016-12-03更新
|
2344次组卷
|
3卷引用:2015年全国普通高等学校招生统一考试数学(江苏卷)
8 . 已知函数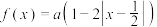 ,a为常数且
,a为常数且 .
.
(1)证明:函数 的图像关于直线
的图像关于直线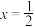 对称;
对称;
(2)若 满足
满足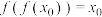 ,但
,但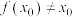 ,则
,则 称为函数
称为函数 的二阶周期点,如果
的二阶周期点,如果 有两个二阶周期点
有两个二阶周期点 ,
, ,试确定a的取值范围;
,试确定a的取值范围;
(3)对于(2)中的 ,
, ,和a,设
,和a,设 为函数
为函数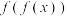 的最大值点,
的最大值点,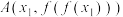 ,
,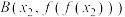 ,
,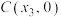 ,记
,记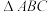 的面积为
的面积为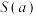 ,讨论
,讨论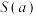 的单调性.
的单调性.
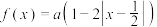 ,a为常数且
,a为常数且 .
.(1)证明:函数
 的图像关于直线
的图像关于直线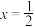 对称;
对称;(2)若
 满足
满足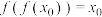 ,但
,但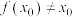 ,则
,则 称为函数
称为函数 的二阶周期点,如果
的二阶周期点,如果 有两个二阶周期点
有两个二阶周期点 ,
, ,试确定a的取值范围;
,试确定a的取值范围;(3)对于(2)中的
 ,
, ,和a,设
,和a,设 为函数
为函数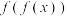 的最大值点,
的最大值点,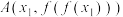 ,
,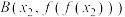 ,
,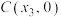 ,记
,记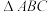 的面积为
的面积为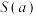 ,讨论
,讨论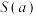 的单调性.
的单调性.
您最近一年使用:0次
2016-12-12更新
|
4247次组卷
|
4卷引用:2013年普通高等学校招生全国统一考试理科数学(江西卷)
2013年普通高等学校招生全国统一考试理科数学(江西卷)(已下线)2019高考备考一轮复习精品资料【理】专题四 函数及其表示 教学案湖南省长沙市同升湖高级中学2025届高三上学期第二次月考数学试题四川省成都市第十七中学2025届高三上学期10月月考数学试题
真题
9 . 设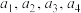 是各项为正数且公差为d
是各项为正数且公差为d 的等差数列
的等差数列
(1)证明: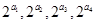 依次成等比数列;
依次成等比数列;
(2)是否存在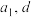 ,使得
,使得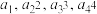 依次成等比数列,并说明理由;
依次成等比数列,并说明理由;
(3)是否存在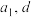 及正整数
及正整数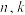 ,使得
,使得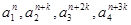 依次成等比数列,并说明理由.
依次成等比数列,并说明理由.
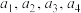 是各项为正数且公差为d
是各项为正数且公差为d 的等差数列
的等差数列(1)证明:
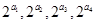 依次成等比数列;
依次成等比数列;(2)是否存在
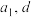 ,使得
,使得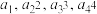 依次成等比数列,并说明理由;
依次成等比数列,并说明理由;(3)是否存在
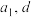 及正整数
及正整数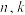 ,使得
,使得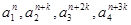 依次成等比数列,并说明理由.
依次成等比数列,并说明理由.
您最近一年使用:0次
10 . 设椭圆 过点
过点  ,且左焦点为
,且左焦点为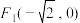
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)当过点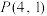 的动直线
的动直线  与椭圆
与椭圆 相交与两不同点
相交与两不同点  时,在线段
时,在线段 上取点
上取点  ,满足
,满足 ,证明:点
,证明:点  总在某定直线上
总在某定直线上
 过点
过点  ,且左焦点为
,且左焦点为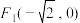
(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)当过点
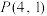 的动直线
的动直线  与椭圆
与椭圆 相交与两不同点
相交与两不同点  时,在线段
时,在线段 上取点
上取点  ,满足
,满足 ,证明:点
,证明:点  总在某定直线上
总在某定直线上
您最近一年使用:0次
2016-11-30更新
|
7629次组卷
|
14卷引用:2008年普通高等学校招生全国统一考试理科数学(安徽卷)
2008年普通高等学校招生全国统一考试理科数学(安徽卷)2008 年普通高等学校招生考试数学(理)试题(安徽卷)(已下线)2014届重庆市第八中学高三第四次月考理科数学试卷【全国百强校】四川省南充市阆中中学2018-2019学年高二3月月考理科数学试题【全国百强校】四川省南充市阆中中学2018-2019学年高二3月月考文科数学试题沪教版(上海) 高三年级 新高考辅导与训练 第十一章 圆锥曲线 三、参数方程(已下线)专题12 解析几何中的定值、定点和定线问题 第一篇 热点、难点突破篇(讲)-2021年高考数学二轮复习讲练测(浙江专用)(已下线)专题7 圆锥曲线之极点与极线 微点1 圆锥曲线之极点与极线(已下线)专题7 圆锥曲线之极点与极线 微点2 极点与极线问题常见模型总结(已下线)专题41 定比点差法、齐次化、极点极线问题、蝴蝶问题(已下线)第五篇 向量与几何 专题5 调和点列 微点2 调和点列(二)(已下线)第五篇 向量与几何 专题6 调和线束 微点1 调和线束(一)(已下线)专题18 圆锥曲线高频压轴解答题(16大核心考点)(讲义)-2(已下线)大招16极点极线



