1 . 由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果椭圆 的“特征三角形”为
的“特征三角形”为 ,椭圆
,椭圆 的“特征三角形”为
的“特征三角形”为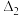 ,若
,若 ,则称椭圆
,则称椭圆 与
与 “相似”,并将
“相似”,并将 与
与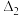 的相似比称为椭圆
的相似比称为椭圆 与
与 的相似比.已知椭圆
的相似比.已知椭圆 :
: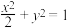 与椭圆
与椭圆 :
: 相似.
相似.
(1)求椭圆 的离心率;
的离心率;
(2)若椭圆 与椭圆
与椭圆 的相似比为
的相似比为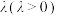 ,设
,设 为
为 上异于其左、右顶点
上异于其左、右顶点 ,
, 的一点.
的一点.
①当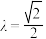 时,过
时,过 分别作椭圆
分别作椭圆 的两条切线
的两条切线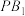 ,
,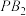 ,切点分别为
,切点分别为 ,
, ,设直线
,设直线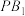 ,
,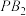 的斜率为
的斜率为 ,
, ,证明:
,证明: 为定值;
为定值;
②当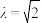 时,若直线
时,若直线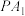 与
与 交于
交于 ,
, 两点,直线
两点,直线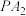 与
与 交于
交于 ,
, 两点,求
两点,求 的值.
的值.
 的“特征三角形”为
的“特征三角形”为 ,椭圆
,椭圆 的“特征三角形”为
的“特征三角形”为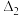 ,若
,若 ,则称椭圆
,则称椭圆 与
与 “相似”,并将
“相似”,并将 与
与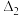 的相似比称为椭圆
的相似比称为椭圆 与
与 的相似比.已知椭圆
的相似比.已知椭圆 :
: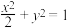 与椭圆
与椭圆 :
: 相似.
相似.(1)求椭圆
 的离心率;
的离心率;(2)若椭圆
 与椭圆
与椭圆 的相似比为
的相似比为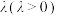 ,设
,设 为
为 上异于其左、右顶点
上异于其左、右顶点 ,
, 的一点.
的一点.①当
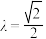 时,过
时,过 分别作椭圆
分别作椭圆 的两条切线
的两条切线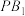 ,
,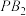 ,切点分别为
,切点分别为 ,
, ,设直线
,设直线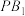 ,
,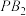 的斜率为
的斜率为 ,
, ,证明:
,证明: 为定值;
为定值;②当
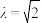 时,若直线
时,若直线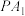 与
与 交于
交于 ,
, 两点,直线
两点,直线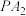 与
与 交于
交于 ,
, 两点,求
两点,求 的值.
的值.
您最近一年使用:0次
2024-03-29更新
|
883次组卷
|
3卷引用:山西省长治市2023-2024学年高二下学期3月质量检测数学试题
2 . 已知 ,且
,且 ,函数
,函数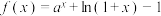 .
.
(1)记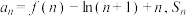 为数列
为数列 的前
的前 项和.证明:当
项和.证明:当 时,
时, ;
;
(2)若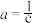 ,证明:
,证明: ;
;
(3)若 有3个零点,求实数
有3个零点,求实数 的取值范围.
的取值范围.
 ,且
,且 ,函数
,函数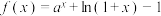 .
.(1)记
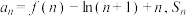 为数列
为数列 的前
的前 项和.证明:当
项和.证明:当 时,
时, ;
;(2)若
 ,证明:
,证明: ;
;(3)若
 有3个零点,求实数
有3个零点,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
3 . 群的概念由法国天才数学家伽罗瓦(1811-1832)在19世纪30年代开创,群论虽起源于对代数多项式方程的研究,但在量子力学、晶体结构学等其他学科中也有十分广泛的应用.设 是一个非空集合,“
是一个非空集合,“ ”是一个适用于
”是一个适用于 中元素的运算,若同时满足以下四个条件,则称
中元素的运算,若同时满足以下四个条件,则称 对“
对“ ”构成一个群:(1)封闭性,即若
”构成一个群:(1)封闭性,即若 ,则存在唯一确定的
,则存在唯一确定的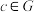 ,使得
,使得 ;(2)结合律成立,即对
;(2)结合律成立,即对 中任意元素
中任意元素 都有
都有 ;(3)单位元存在,即存在
;(3)单位元存在,即存在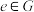 ,对任意
,对任意 ,满足
,满足 ,则
,则 称为单位元;(4)逆元存在,即任意
称为单位元;(4)逆元存在,即任意 ,存在
,存在 ,使得
,使得 ,则称
,则称 与
与 互为逆元,
互为逆元, 记作
记作 .一般地,
.一般地, 可简记作
可简记作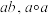 可简记作
可简记作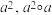 可简记作
可简记作 ,以此类推.正八边形
,以此类推.正八边形 的中心为
的中心为 .以
.以 表示恒等变换,即不对正八边形作任何变换;以
表示恒等变换,即不对正八边形作任何变换;以 表示以点
表示以点 为中心,将正八边形逆时针旋转
为中心,将正八边形逆时针旋转 的旋转变换;以
的旋转变换;以 表示以
表示以 所在直线为轴,将正八边形进行轴对称变换.定义运算“
所在直线为轴,将正八边形进行轴对称变换.定义运算“ ”表示复合变换,即
”表示复合变换,即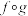 表示将正八边形先进行
表示将正八边形先进行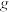 变换再进行
变换再进行 变换的变换.以形如
变换的变换.以形如 ,并规定
,并规定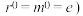 的变换为元素,可组成集合
的变换为元素,可组成集合 ,则
,则 对运算“
对运算“ ”可构成群,称之为“正八边形的对称变换群”,记作
”可构成群,称之为“正八边形的对称变换群”,记作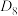 .则以下关于
.则以下关于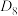 及其元素的说法中,正确的有( )
及其元素的说法中,正确的有( )
 是一个非空集合,“
是一个非空集合,“ ”是一个适用于
”是一个适用于 中元素的运算,若同时满足以下四个条件,则称
中元素的运算,若同时满足以下四个条件,则称 对“
对“ ”构成一个群:(1)封闭性,即若
”构成一个群:(1)封闭性,即若 ,则存在唯一确定的
,则存在唯一确定的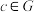 ,使得
,使得 ;(2)结合律成立,即对
;(2)结合律成立,即对 中任意元素
中任意元素 都有
都有 ;(3)单位元存在,即存在
;(3)单位元存在,即存在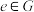 ,对任意
,对任意 ,满足
,满足 ,则
,则 称为单位元;(4)逆元存在,即任意
称为单位元;(4)逆元存在,即任意 ,存在
,存在 ,使得
,使得 ,则称
,则称 与
与 互为逆元,
互为逆元, 记作
记作 .一般地,
.一般地, 可简记作
可简记作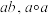 可简记作
可简记作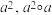 可简记作
可简记作 ,以此类推.正八边形
,以此类推.正八边形 的中心为
的中心为 .以
.以 表示恒等变换,即不对正八边形作任何变换;以
表示恒等变换,即不对正八边形作任何变换;以 表示以点
表示以点 为中心,将正八边形逆时针旋转
为中心,将正八边形逆时针旋转 的旋转变换;以
的旋转变换;以 表示以
表示以 所在直线为轴,将正八边形进行轴对称变换.定义运算“
所在直线为轴,将正八边形进行轴对称变换.定义运算“ ”表示复合变换,即
”表示复合变换,即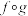 表示将正八边形先进行
表示将正八边形先进行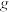 变换再进行
变换再进行 变换的变换.以形如
变换的变换.以形如 ,并规定
,并规定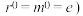 的变换为元素,可组成集合
的变换为元素,可组成集合 ,则
,则 对运算“
对运算“ ”可构成群,称之为“正八边形的对称变换群”,记作
”可构成群,称之为“正八边形的对称变换群”,记作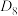 .则以下关于
.则以下关于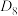 及其元素的说法中,正确的有( )
及其元素的说法中,正确的有( )A.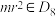 ,且 ,且 |
B. 与 与 互为逆元 互为逆元 |
C.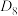 中有无穷多个元素 中有无穷多个元素 |
D.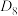 中至少存在三个不同的元素,它们的逆元都是其本身 中至少存在三个不同的元素,它们的逆元都是其本身 |
您最近一年使用:0次
名校
解题方法
4 . 悬链线的原理运用于悬索桥、架空电缆、双曲拱桥、拱坝等工程.通过适当建立坐标系,悬链线可为双曲余弦函数 的图象,类比三角函数的三种性质:①平方关系:①
的图象,类比三角函数的三种性质:①平方关系:①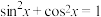 ,②和角公式:
,②和角公式: ,③导数:
,③导数: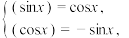 定义双曲正弦函数
定义双曲正弦函数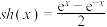 .
.
(1)直接写出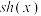 ,
,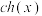 具有的类似①、②、③的三种性质(不需要证明);
具有的类似①、②、③的三种性质(不需要证明);
(2)若当 时,
时, 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)求 的最小值.
的最小值.
 的图象,类比三角函数的三种性质:①平方关系:①
的图象,类比三角函数的三种性质:①平方关系:①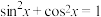 ,②和角公式:
,②和角公式: ,③导数:
,③导数: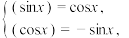 定义双曲正弦函数
定义双曲正弦函数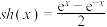 .
.(1)直接写出
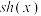 ,
,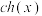 具有的类似①、②、③的三种性质(不需要证明);
具有的类似①、②、③的三种性质(不需要证明);(2)若当
 时,
时, 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;(3)求
 的最小值.
的最小值.
您最近一年使用:0次
2024-01-27更新
|
1993次组卷
|
7卷引用:2024届山西省平遥县第二中学校高三冲刺调研押题卷数学(二)
2024届山西省平遥县第二中学校高三冲刺调研押题卷数学(二)云南省昆明市第一中学2024届高三上学期第六次考前基础强化数学试题2024届高三新改革适应性模拟测试数学试卷一(九省联考题型)浙江省湖州市第一中学2024届高三下学期新高考数学模拟试题(已下线)压轴题函数与导数新定义题(九省联考第19题模式)练(已下线)微考点2-5 新高考新试卷结构19题压轴题新定义导数试题分类汇编江苏省常州高级中学2023-2024学年高二下学期第一次调研考试数学试题



