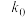1 . 某个地区从某年起几年内的新生婴儿数及其中男婴数如下表:
(1)填写表中的男婴出生频率;(保留两位有效数字)
(2)这一地区男婴出生的概率约是______ .
(1)填写表中的男婴出生频率;(保留两位有效数字)
时间范围 | 1年内 | 2年内 | 3年内 | 4年内 |
新生婴儿数 | 5544 | 9013 | 13520 | 17191 |
男婴数 | 2716 | 4899 | 6812 | 8590 |
男婴出生频率 |
您最近一年使用:0次
2023-02-06更新
|
515次组卷
|
9卷引用:12.3 频率与概率(三大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020必修第三册)
(已下线)12.3 频率与概率(三大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020必修第三册)人教A版2017-2018学年必修三第三章3.1-3.1.1随机事件的概率2数学试题沪教版(2020) 必修第三册 高效课堂 第十二章 12.3 频率与概率(已下线)10.3频率与概率(10.3.1 频率的稳定性+10.3.2 随机模拟) (精讲)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)(已下线)10.3 频率与概率(精讲)-2022-2023学年高一数学一隅三反系列(人教A版2019必修第二册)第十章《概率》单元达标高分突破必刷卷(基础版)-《考点·题型·技巧》(已下线)第十章:概率 重点题型复习(2) --【题型分类归纳】(已下线)第15章:概率 重点题型复习-【题型分类归纳】(苏教版2019必修第二册)(已下线)10.3.1&10.3.2?频率的稳定性、随机模拟——课堂例题
2 . 对变量 有观测数据
有观测数据 (
(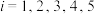 ),得表1;对变量
),得表1;对变量 有观测数据
有观测数据 (
(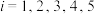 ),得表2.由这两个表可以判断:变量x与y
),得表2.由这两个表可以判断:变量x与y______ ,变量u与v______ .(填写“正相关”或“负相关”)
表1
表2
 有观测数据
有观测数据 (
(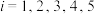 ),得表1;对变量
),得表1;对变量 有观测数据
有观测数据 (
(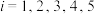 ),得表2.由这两个表可以判断:变量x与y
),得表2.由这两个表可以判断:变量x与y表1
x | 1 | 2 | 3 | 4 | 5 |
y | 2.9 | 3.3 | 3.6 | 4.4 | 5.1 |
u | 1 | 2 | 3 | 4 | 5 |
v | 25 | 20 | 21 | 15 | 13 |
您最近一年使用:0次
2023-01-03更新
|
212次组卷
|
4卷引用:沪教版(2020) 选修第二册 堂堂清 第8章 单元复习八
23-24高二上·全国·课后作业
3 . 根据通项公式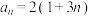 ,填写下表:
,填写下表:
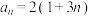 ,填写下表:
,填写下表:n | 1 | 2 | 3 | … | 11 | … | … | ||
 | … | … | 128 | … | 602 |
您最近一年使用:0次
23-24高二上·全国·课后作业
4 . 已知数列 是公比为
是公比为 的等比数列,试根据所给条件填写下表:
的等比数列,试根据所给条件填写下表:
 是公比为
是公比为 的等比数列,试根据所给条件填写下表:
的等比数列,试根据所给条件填写下表:| 题号 |  |  |  |  |
| (1) | 0.03 | 9 | 6 | |
| (2) |  | 7 | 32 | |
| (3) | 1 | 2 | 256 |
您最近一年使用:0次
5 . 以下问题中,适合使用简单随机抽样的是______ .(填写编号)
①某市人均寿命调查;②某高一年级学生体能素质调查;③30个灯泡的使用寿命调查.
①某市人均寿命调查;②某高一年级学生体能素质调查;③30个灯泡的使用寿命调查.
您最近一年使用:0次
2022-09-15更新
|
245次组卷
|
2卷引用:【课后练】13.3 抽样方法课后作业-沪教版(2020)必修第三册第13章 统计
6 . 为了检测甲、乙两名工人生产的产品是否合格,一共抽取了40件产品进行测量,其中甲产品20件,乙产品20件,分别称量产品的重量(单位:克),记重量不低于66克的产品为“合格”,作出茎叶图如图:
(2)根据茎叶图填写下面的列联表,并判断能否有 的把握认为产品是否合格与生产的工人有关?
的把握认为产品是否合格与生产的工人有关?
附:
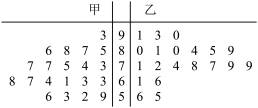
(2)根据茎叶图填写下面的列联表,并判断能否有
 的把握认为产品是否合格与生产的工人有关?
的把握认为产品是否合格与生产的工人有关?甲 | 乙 | 合计 | |
合格 | |||
不合格 | |||
合计 |

| 0.15 | 0.10 | 0.05 |
| 2.072 | 2.706 | 3.841 |
您最近一年使用:0次
2023-03-14更新
|
472次组卷
|
4卷引用:9.2独立性检验(1)
7 . 已知变量x和y满足关系 ,变量y与z负相关,则可以判断变量x与y
,变量y与z负相关,则可以判断变量x与y______ ,x与z______ .(填写“正相关”或“负相关”)
 ,变量y与z负相关,则可以判断变量x与y
,变量y与z负相关,则可以判断变量x与y
您最近一年使用:0次
名校
解题方法
8 . 热心网友们调查统计了柳州市某网红景点在2022年6月至10月的旅游收入y(单位:万元),得到以下数据:
(1)根据表中所给数据,用相关系数r加以判断,是否可用线性回归模型拟合y与x的关系?若可以,求出y关于x之间的线性回归方程;若不可以,请说明理由;
(2)为调查游客对该景点的评价情况,网友们随机抽查了200名游客,得到如图列联表,请填写2×2列联表,并判断能否有99.9%的把握认为“游客是否喜欢该网红景点与性别有关联”?
参考数据: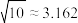 ,
,
注:r与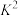 的计算结果精确到0.001.参考公式:相关系数
的计算结果精确到0.001.参考公式:相关系数 ,
,
线性回归方程: ,其中
,其中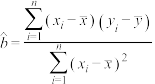 ,
, ,
,
 .
.
临界值表:
月份x | 6 | 7 | 8 | 9 | 10 |
旅游收入y | 10 | 12 | 11 | 12 | 20 |
(2)为调查游客对该景点的评价情况,网友们随机抽查了200名游客,得到如图列联表,请填写2×2列联表,并判断能否有99.9%的把握认为“游客是否喜欢该网红景点与性别有关联”?
喜欢 | 不喜欢 | 总计 | |
男 | 100 | ||
女 | 60 | ||
总计 | 110 |
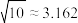 ,
,注:r与
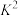 的计算结果精确到0.001.参考公式:相关系数
的计算结果精确到0.001.参考公式:相关系数 ,
,线性回归方程:
 ,其中
,其中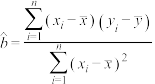 ,
, ,
, .
.临界值表:
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2023-01-18更新
|
502次组卷
|
7卷引用:8.3 列联表与独立性检验(精练)
(已下线)8.3 列联表与独立性检验(精练)(已下线)8.3.1分类变量与列联表(分层作业)广西“智桂杯”2022届高三上学期大数据精准诊断性大联考数学(理)试题(已下线)专题3.1 模拟卷(1)-2022年高考数学大数据精选模拟卷(新高考地区专用)河南省信阳市普通高中2022-2023学年高三第二次教学质量检测数学(文科)试题四川省内江市威远中学校2022-2023学年高三下学期第一次月考数学(文)试题(已下线)第四章 统计 专题三 独立性检验 微点3 独立性检验(三)【培优版】
9 . 判断下列说法是否正确,正确的在括号中填写正确,错误的填错误
(1)相关关系与函数关系都是一种确定性的关系,也是一种因果关系.( )
(2)利用散点图可以直观判断两个变量的关系是否可以用线性关系表示.( )
(3)线性相关系数r越大,两个变量的线性相关性越强.( )
(4)线性相关系数r越小,两个变量的线性相关性越弱.( )
(5)用相关系数r来刻画回归效果,r越小,说明模型的拟合效果越好.( )
(1)相关关系与函数关系都是一种确定性的关系,也是一种因果关系.
(2)利用散点图可以直观判断两个变量的关系是否可以用线性关系表示.
(3)线性相关系数r越大,两个变量的线性相关性越强.
(4)线性相关系数r越小,两个变量的线性相关性越弱.
(5)用相关系数r来刻画回归效果,r越小,说明模型的拟合效果越好.
您最近一年使用:0次
名校
10 . 为了检测产品质量,某企业从甲、乙两条生产线上分别抽取 件产品作为样本,检测其质量指标值,质量指标值的范围为
件产品作为样本,检测其质量指标值,质量指标值的范围为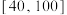 .根据该产品的质量标准,规定质量指标值在
.根据该产品的质量标准,规定质量指标值在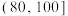 内的产品为“优等品”,否则为“非优等品”.抽样统计后得到的数据如下:
内的产品为“优等品”,否则为“非优等品”.抽样统计后得到的数据如下:
(1)填写下面的 列联表,计算
列联表,计算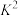 ,并判断能否有
,并判断能否有 的把握认为产品是否为“优等品”与生产线有关;
的把握认为产品是否为“优等品”与生产线有关;
(2)由于样本中来自乙生产线“非优等品”的个数多于来自甲生产线的,为找出原因,该厂质量控制部门在抽出的“非优等品”中,按甲、乙生产线采用分层抽样的方法抽出 件产品,然后再从中随机抽出
件产品,然后再从中随机抽出 件产品进行全面分析,求其中至少有
件产品进行全面分析,求其中至少有 件是乙生产线生产的产品的概率.
件是乙生产线生产的产品的概率.
附: ,
, .
.
 件产品作为样本,检测其质量指标值,质量指标值的范围为
件产品作为样本,检测其质量指标值,质量指标值的范围为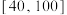 .根据该产品的质量标准,规定质量指标值在
.根据该产品的质量标准,规定质量指标值在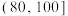 内的产品为“优等品”,否则为“非优等品”.抽样统计后得到的数据如下:
内的产品为“优等品”,否则为“非优等品”.抽样统计后得到的数据如下:| 质量指标值 | 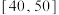 | 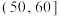 | 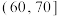 | 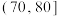 | 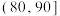 | 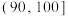 |
| 甲生产线生产的产品数量 |  |  | 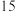 |  |  | 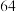 |
| 乙生产线生产的产品数量 |  |  |  | 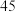 |  |  |
 列联表,计算
列联表,计算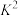 ,并判断能否有
,并判断能否有 的把握认为产品是否为“优等品”与生产线有关;
的把握认为产品是否为“优等品”与生产线有关;| 优等品 | 非优等品 | 合计 | |
| 甲生产线生产的产品数量 | |||
| 乙生产线生产的产品数量 | |||
| 合计 |
 件产品,然后再从中随机抽出
件产品,然后再从中随机抽出 件产品进行全面分析,求其中至少有
件产品进行全面分析,求其中至少有 件是乙生产线生产的产品的概率.
件是乙生产线生产的产品的概率.附:
 ,
, .
. | 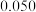 |  |  |
| k |  |  |  |
您最近一年使用:0次
2022-12-29更新
|
644次组卷
|
5卷引用:8.3 列联表与独立性检验 (精讲)
(已下线)8.3 列联表与独立性检验 (精讲)河南省2022-2023年度高三模拟考试数学(文科)试题(已下线)专题10 概率与统计的综合运用(精讲精练)-2四川省成都市成都外国语学校2022-2023学年高三上学期期末数学文科试题(已下线)第四章 统计 专题五 独立性检验 微点1 独立性检验(一)【基础版】