1 . 判断下列说法是否正确,正确的在括号中填写正确,错误的填错误
(1)相关关系与函数关系都是一种确定性的关系,也是一种因果关系.( )
(2)利用散点图可以直观判断两个变量的关系是否可以用线性关系表示.( )
(3)线性相关系数r越大,两个变量的线性相关性越强.( )
(4)线性相关系数r越小,两个变量的线性相关性越弱.( )
(5)用相关系数r来刻画回归效果,r越小,说明模型的拟合效果越好.( )
(1)相关关系与函数关系都是一种确定性的关系,也是一种因果关系.
(2)利用散点图可以直观判断两个变量的关系是否可以用线性关系表示.
(3)线性相关系数r越大,两个变量的线性相关性越强.
(4)线性相关系数r越小,两个变量的线性相关性越弱.
(5)用相关系数r来刻画回归效果,r越小,说明模型的拟合效果越好.
您最近一年使用:0次
名校
2 . 为了检测产品质量,某企业从甲、乙两条生产线上分别抽取 件产品作为样本,检测其质量指标值,质量指标值的范围为
件产品作为样本,检测其质量指标值,质量指标值的范围为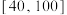 .根据该产品的质量标准,规定质量指标值在
.根据该产品的质量标准,规定质量指标值在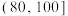 内的产品为“优等品”,否则为“非优等品”.抽样统计后得到的数据如下:
内的产品为“优等品”,否则为“非优等品”.抽样统计后得到的数据如下:
(1)填写下面的 列联表,计算
列联表,计算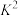 ,并判断能否有
,并判断能否有 的把握认为产品是否为“优等品”与生产线有关;
的把握认为产品是否为“优等品”与生产线有关;
(2)由于样本中来自乙生产线“非优等品”的个数多于来自甲生产线的,为找出原因,该厂质量控制部门在抽出的“非优等品”中,按甲、乙生产线采用分层抽样的方法抽出 件产品,然后再从中随机抽出
件产品,然后再从中随机抽出 件产品进行全面分析,求其中至少有
件产品进行全面分析,求其中至少有 件是乙生产线生产的产品的概率.
件是乙生产线生产的产品的概率.
附: ,
, .
.
 件产品作为样本,检测其质量指标值,质量指标值的范围为
件产品作为样本,检测其质量指标值,质量指标值的范围为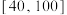 .根据该产品的质量标准,规定质量指标值在
.根据该产品的质量标准,规定质量指标值在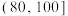 内的产品为“优等品”,否则为“非优等品”.抽样统计后得到的数据如下:
内的产品为“优等品”,否则为“非优等品”.抽样统计后得到的数据如下:| 质量指标值 | 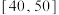 | 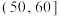 | 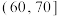 | 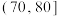 | 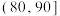 | 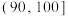 |
| 甲生产线生产的产品数量 |  |  | 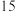 |  |  | 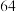 |
| 乙生产线生产的产品数量 |  |  |  | 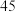 |  |  |
 列联表,计算
列联表,计算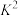 ,并判断能否有
,并判断能否有 的把握认为产品是否为“优等品”与生产线有关;
的把握认为产品是否为“优等品”与生产线有关;| 优等品 | 非优等品 | 合计 | |
| 甲生产线生产的产品数量 | |||
| 乙生产线生产的产品数量 | |||
| 合计 |
 件产品,然后再从中随机抽出
件产品,然后再从中随机抽出 件产品进行全面分析,求其中至少有
件产品进行全面分析,求其中至少有 件是乙生产线生产的产品的概率.
件是乙生产线生产的产品的概率.附:
 ,
, .
. | 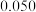 |  |  |
| k |  |  |  |
您最近一年使用:0次
2022-12-29更新
|
644次组卷
|
5卷引用:8.3 列联表与独立性检验 (精讲)
(已下线)8.3 列联表与独立性检验 (精讲)河南省2022-2023年度高三模拟考试数学(文科)试题(已下线)专题10 概率与统计的综合运用(精讲精练)-2四川省成都市成都外国语学校2022-2023学年高三上学期期末数学文科试题(已下线)第四章 统计 专题五 独立性检验 微点1 独立性检验(一)【基础版】
解题方法
3 . 在棱长为1的正方体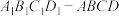 中,
中, 为底面
为底面 的中心,
的中心, 是棱
是棱 上一点,且
上一点,且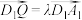 ,
,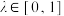 ,
, 为线段
为线段 的中点,给出下列命题:
的中点,给出下列命题: 四点共面;
四点共面;
②三棱锥 的体积与
的体积与 的取值有关;
的取值有关;
③当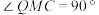 时,
时, ;
;
④当 时,过
时,过 三点的平面截正方体所得截面的面积为
三点的平面截正方体所得截面的面积为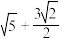 .
.
其中正确的有__________ (填写序号).
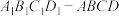 中,
中, 为底面
为底面 的中心,
的中心, 是棱
是棱 上一点,且
上一点,且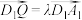 ,
,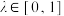 ,
, 为线段
为线段 的中点,给出下列命题:
的中点,给出下列命题: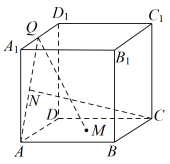
 四点共面;
四点共面;②三棱锥
 的体积与
的体积与 的取值有关;
的取值有关;③当
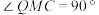 时,
时, ;
;④当
 时,过
时,过 三点的平面截正方体所得截面的面积为
三点的平面截正方体所得截面的面积为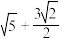 .
.其中正确的有
您最近一年使用:0次
2022-12-10更新
|
281次组卷
|
4卷引用:6.3.3空间角的计算(2)
4 . 在某网店购买之前未曾使用过的商品时,先翻看该商品的相关评价.从统计角度来看,这也是一种抽样调查,这种抽样调查______ .(填写“具有代表性”“不具有代表性”)请说明理由.
您最近一年使用:0次
5 . 2021年10月16日,搭载“神舟十三号”的火箭发射升空,这是一件让全国人民普遍关注的大事,因此每天有很多民众通过手机、电视等方式观看有关新闻.某机构将每天关注这件大事的时间在2小时以上的人称为“天文爱好者”,否则称为“非天文爱好者”,该机构通过调查,并从参与调查的人群中随机抽取了100人进行分析,得到下表(单位:人)
附: ,其中
,其中 .
.
(1)将上表中的数据填写完整,并判断能否在犯错误的概率不超过0.005的前提下认为“天文爱好者”或“非天文爱好者”与性别有关?
(2)现从抽取的女性人群中,按“天文爱好者”和“非天文爱好者”这两种类型进行分层抽样抽取5人,然后再从这5人中随机选出3人,求其中至少有1人是“天文爱好者”的概率.
天文爱好者 | 非天文爱好者 | 合计 | |
女 | 20 | 50 | |
男 | 15 | ||
合计 | 100 |
 ,其中
,其中 .
.| α | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(2)现从抽取的女性人群中,按“天文爱好者”和“非天文爱好者”这两种类型进行分层抽样抽取5人,然后再从这5人中随机选出3人,求其中至少有1人是“天文爱好者”的概率.
您最近一年使用:0次
解题方法
6 . 某公司现统计了某产品在2021年7月至11月的总销售量y(单位:万),得到以下数据:
为调查顾客对该产品的接受情况,随机抽查了200名顾客,得到如下列联表,请填写下面的2×2列联表,并判断是否有99%的把握认为“顾客是否接受该产品与性别有关”.
月份x | 7 | 8 | 9 | 10 | 11 |
销售量y | 10 | 12 | 11 | 12 | 20 |
接受 | 不接受 | 总计 | |
男 | 100 | ||
女 | 60 | ||
总计 | 110 |
您最近一年使用:0次
2022-09-13更新
|
64次组卷
|
2卷引用:沪教版(2020) 选修第二册 经典学案 第8章 8.3 2×2列联表
7 . 已知某区A,B两所学校的高二年级在校学生人数之比为9:11,现用分层抽样的方法从A,B两校高二年级在校学生中共抽取了100名学生,调查了他们课后做作业的时间,并根据调查结果绘制了如下频率分布直方图:
(2)如果要了解学生做作业时间的平均时长(同一组中的数据用该组区间的中点值作代表)和做作业时长超过3小时的学生比例,请根据频率分布直方图,估计这两个数值;
(3)另据调查,这100人中做作业时间超过3小时的有20人来自A中学,根据已知条件填写下面列联表,并根据列联表判断是否有99%的把握认为“做作业时间超过3小时”与“学校”有关?
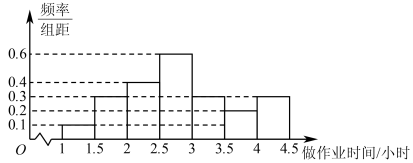
(2)如果要了解学生做作业时间的平均时长(同一组中的数据用该组区间的中点值作代表)和做作业时长超过3小时的学生比例,请根据频率分布直方图,估计这两个数值;
(3)另据调查,这100人中做作业时间超过3小时的有20人来自A中学,根据已知条件填写下面列联表,并根据列联表判断是否有99%的把握认为“做作业时间超过3小时”与“学校”有关?
做作业时间超过3小时 | 做作业时间不超过3小时 | 合计 | |
A校 | |||
B校 | |||
合计 |
您最近一年使用:0次
2022-09-13更新
|
115次组卷
|
2卷引用:沪教版(2020) 选修第二册 经典学案 第8章 8.3 2×2列联表
解题方法
8 . 已知中学生综合素质评价的某个维度分“优秀、合格、尚待改进”三个等级,某校在某次测评中采用的是学生互评的方式.若该校高二年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样的方法从高二年级抽取了45名学生,了解他们的测评结果,并列出频数统计表如下:
表1:男生
表2:女生
(1)确定表中x,y的值,并填写下面的2×2列联表:
(2)根据(1)中所列2×2列联表,判断是否有90%的把握认为“测评结果优秀与性别有关”.
参考公式: 其中
其中 .
.
临界值表:
表1:男生
等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 | x | 5 |
等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 | 3 | y |
男生 | 女生 | 合计 | |
优秀 | |||
非优秀 | |||
合计 |
参考公式:
 其中
其中 .
.临界值表:
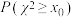 | 0.1 | 0.05 | 0.01 |
 | 2.706 | 3.841 | 6.635 |
您最近一年使用:0次
9 . 在长方体 中,下列各线段所在直线的位置关系分别为:(填写:相交、平行或异面)
中,下列各线段所在直线的位置关系分别为:(填写:相交、平行或异面)
(1) 和
和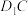 是
是______ 直线;
(2) 和
和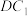 是
是______ 直线;
(3) 和
和 是
是______ 直线;
(4) 和
和 是
是______ 直线.
 中,下列各线段所在直线的位置关系分别为:(填写:相交、平行或异面)
中,下列各线段所在直线的位置关系分别为:(填写:相交、平行或异面)(1)
 和
和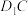 是
是(2)
 和
和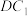 是
是(3)
 和
和 是
是(4)
 和
和 是
是
您最近一年使用:0次
2022-09-15更新
|
132次组卷
|
2卷引用:【课后练】10.2.2 异面直线 课后作业-沪教版(2020)必修第三册第10章 空间直线与平面
10 . 若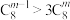 ,则
,则 的取值可能为
的取值可能为______ .(填写一个符合题意的数值即可)
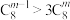 ,则
,则 的取值可能为
的取值可能为
您最近一年使用:0次



