解题方法
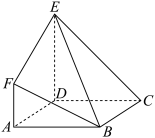
1 . 如图,在多面体 中,四边形
中,四边形 是菱形,
是菱形, 平面
平面 ,
,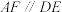 ,
, ,
,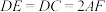 .
. 平面
平面 ;
;
(2)线段 上是否存在点
上是否存在点 ,使得
,使得 ∥平面
∥平面 ?若存在,指出点
?若存在,指出点 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
 中,四边形
中,四边形 是菱形,
是菱形, 平面
平面 ,
,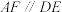 ,
, ,
,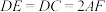 .
.
 平面
平面 ;
;(2)线段
 上是否存在点
上是否存在点 ,使得
,使得 ∥平面
∥平面 ?若存在,指出点
?若存在,指出点 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
您最近一年使用:0次
名校
解题方法
2 . 设实系数一元二次方程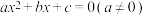 ①,有两根
①,有两根 ,
,
则方程可变形为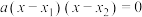 ,展开得
,展开得 ②,
②,
比较①②可以得到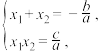
这表明,任何一个一元二次方程的根与系数的关系为:两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比.这就是我们熟知的一元二次方程的韦达定理.
事实上,与二次方程类似,一元三次方程也有韦达定理.
设方程 有三个根
有三个根 ,则有
,则有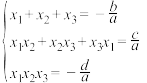 ③
③
(1)证明公式③,即一元三次方程的韦达定理;
(2)已知函数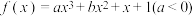 恰有两个零点.
恰有两个零点.
(i)求证: 的其中一个零点大于0,另一个零点大于
的其中一个零点大于0,另一个零点大于 且小于0;
且小于0;
(ii)求 的取值范围.
的取值范围.
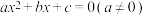 ①,有两根
①,有两根 ,
,则方程可变形为
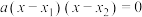 ,展开得
,展开得 ②,
②,比较①②可以得到
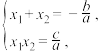
这表明,任何一个一元二次方程的根与系数的关系为:两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比.这就是我们熟知的一元二次方程的韦达定理.
事实上,与二次方程类似,一元三次方程也有韦达定理.
设方程
 有三个根
有三个根 ,则有
,则有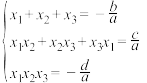 ③
③(1)证明公式③,即一元三次方程的韦达定理;
(2)已知函数
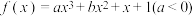 恰有两个零点.
恰有两个零点.(i)求证:
 的其中一个零点大于0,另一个零点大于
的其中一个零点大于0,另一个零点大于 且小于0;
且小于0;(ii)求
 的取值范围.
的取值范围.
您最近一年使用:0次
2024-04-18更新
|
606次组卷
|
6卷引用:四川省成都市第七中学20232024学年高二下学期期末考试数学试卷
(已下线)四川省成都市第七中学20232024学年高二下学期期末考试数学试卷(已下线)四川省成都市第七中学2023-2024学年高二下学期期末考试数学试卷贵州省贵阳市第一中学2023-2024学年高二下学期教学质量监测卷(三)数学试题(已下线)模块五 专题6 全真拔高模拟6(人教B版高二期中研习)四川省成都市树德中学2024-2025学年高三上学期开学考试数学试题云南省玉溪市玉溪师范学院附属中学2025届高三上学期开学适应性考试数学试卷
名校
3 . 设 ,函数
,函数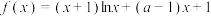 .
.
(1)判断 的零点个数,并证明你的结论;
的零点个数,并证明你的结论;
(2)若 ,记
,记 的一个零点为
的一个零点为 ,若
,若 ,求证:
,求证: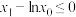 .
.
 ,函数
,函数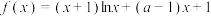 .
.(1)判断
 的零点个数,并证明你的结论;
的零点个数,并证明你的结论;(2)若
 ,记
,记 的一个零点为
的一个零点为 ,若
,若 ,求证:
,求证: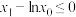 .
.
您最近一年使用:0次
2023-06-02更新
|
600次组卷
|
6卷引用:四川天府新区太平中学2022-2023学年高二毕业班摸底测试(理科)(一)试题
四川天府新区太平中学2022-2023学年高二毕业班摸底测试(理科)(一)试题福建省福州第三中学2023届高三第二十次质量检测数学试题(已下线)第二章 函数的概念与性质 第十节 函数与方程(B素养提升卷)(已下线)第十节 函数与方程(B素养提升卷)安徽省皖东十校联盟2024届高三上学期第三次月考数学试题2024届安徽新高考数学预测模拟卷(七)
名校
解题方法
4 . 已知椭圆 的离心率为
的离心率为 ,设
,设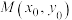 是C上的动点,以M为圆心作一个半径
是C上的动点,以M为圆心作一个半径 的圆,过原点作该圆的两切线分别与椭圆C交于点P、Q,若存在圆M与两坐标轴都相切.
的圆,过原点作该圆的两切线分别与椭圆C交于点P、Q,若存在圆M与两坐标轴都相切.
(2)若直线OP,OQ的斜率都存在且分别为 ,
, ,求证:
,求证: 为定值;
为定值;
(3)证明: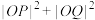 为定值?并求
为定值?并求 的最大值.
的最大值.
 的离心率为
的离心率为 ,设
,设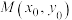 是C上的动点,以M为圆心作一个半径
是C上的动点,以M为圆心作一个半径 的圆,过原点作该圆的两切线分别与椭圆C交于点P、Q,若存在圆M与两坐标轴都相切.
的圆,过原点作该圆的两切线分别与椭圆C交于点P、Q,若存在圆M与两坐标轴都相切.
(2)若直线OP,OQ的斜率都存在且分别为
 ,
, ,求证:
,求证: 为定值;
为定值;(3)证明:
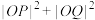 为定值?并求
为定值?并求 的最大值.
的最大值.
您最近一年使用:0次
2022-12-03更新
|
682次组卷
|
4卷引用:四川省泸县第四中学2022-2023学年高二上学期期末考试数学(理)试题
四川省泸县第四中学2022-2023学年高二上学期期末考试数学(理)试题四川省成都市树德中学2022-2023学年高二上学期期中考试数学(文)试题四川省成都市树德中学2022-2023学年高二上学期期中考试数学(理)试题(已下线)重难点突破15 圆锥曲线中的经典七大名圆问题(七大题型)
名校
解题方法
5 . 如图,在四棱锥 中,底面
中,底面 是正方形,过
是正方形,过 的平面与侧棱
的平面与侧棱 的交点分别是
的交点分别是 .
.

(1)证明: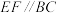 ;
;
(2)若 底面
底面 ,求证:
,求证: 平面
平面 .
.
 中,底面
中,底面 是正方形,过
是正方形,过 的平面与侧棱
的平面与侧棱 的交点分别是
的交点分别是 .
.
(1)证明:
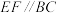 ;
;(2)若
 底面
底面 ,求证:
,求证: 平面
平面 .
.
您最近一年使用:0次
2022-11-02更新
|
731次组卷
|
3卷引用:四川省大英中学2022-2023学年高二上学期期末考试数学(理)试题
6 . 如图所示,在四棱锥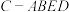 中,四边形
中,四边形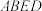 是正方形,点
是正方形,点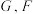 分别是线段
分别是线段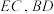 的中点.
的中点.
(1)求证: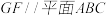 ;
;
(2)线段 上是否存在一点
上是否存在一点 ,使得面
,使得面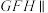 面
面 ,若存在,请找出点
,若存在,请找出点 并证明;若不存在,请说明理由.
并证明;若不存在,请说明理由.
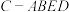 中,四边形
中,四边形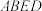 是正方形,点
是正方形,点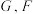 分别是线段
分别是线段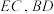 的中点.
的中点.
(1)求证:
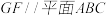 ;
;(2)线段
 上是否存在一点
上是否存在一点 ,使得面
,使得面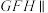 面
面 ,若存在,请找出点
,若存在,请找出点 并证明;若不存在,请说明理由.
并证明;若不存在,请说明理由.
您最近一年使用:0次
2019-01-26更新
|
2637次组卷
|
19卷引用:四川省眉山市2022-2023学年高二上学期期末教学质量检测数学(文)试题
四川省眉山市2022-2023学年高二上学期期末教学质量检测数学(文)试题四川省眉山市2022-2023学年高二上学期期末教学质量检测理科数学试题四川省眉山市2022-2023学年高二上学期期末数学(理)试题【全国百强校】重庆市江津中学、合川中学等七校2018-2019学年高二上学期期末考试数学(理科)试题【校级联考】重庆市江津中学、合川中学等七校2018-2019学年高二上学期期末考试数学(文科)试题四川省峨眉第二中学校2022-2023学年高二上学期10月月考文科数学试题安徽省皖北名校2020-2021学年高二上学期第一次联考数学试题安徽省合肥市肥东县第二中学2020-2021学年高二上学期第一次月考数学(理)试题(已下线)2.2.4 平面与平面平行的性质-2020-2021学年高一数学课时同步练(人教A版必修2)福建省厦门一中2020-2021学年高一下学期期中考数学试题湖南省郴州市嘉禾县第一中学2020-2021学年高一下学期第二次月考数学试题湖北省鄂东南三校联考2021-2022学年高一下学期阶段考试(二)数学试题安徽省芜湖市华星学校2021-2022学年高一下学期期中数学试题陕西省西安市鄠邑区2022-2023学年高一下学期期中数学试题陕西省渭南市韩城市新蕾中学2020-2021学年高一上学期第三次月考数学试题云南省红河州开远市第一中学校2022-2023学年高一下学期4月月考数学试题浙江省嘉兴八校联盟2020-2021学年高一下学期期中联考数学试题(已下线)核心考点07空间直线、平面的平行江苏省无锡市江阴市三校联考2023-2024学年高一下学期4月期中数学试题
名校
7 . 如图,在边长为 的正方形
的正方形 中,点
中,点 是
是 的中点,点
的中点,点 是
是 的中点,点
的中点,点 是
是 上的点,且
上的点,且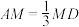 .将△AED,△DCF分别沿
.将△AED,△DCF分别沿 ,
,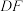 折起,使
折起,使 ,
, 两点重合于
两点重合于 ,连接
,连接 ,
, .
.
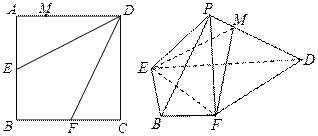
(Ⅰ)求证: ;
;
(Ⅱ)试判断 与平面
与平面 的位置关系,并给出证明.
的位置关系,并给出证明.
 的正方形
的正方形 中,点
中,点 是
是 的中点,点
的中点,点 是
是 的中点,点
的中点,点 是
是 上的点,且
上的点,且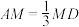 .将△AED,△DCF分别沿
.将△AED,△DCF分别沿 ,
,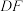 折起,使
折起,使 ,
, 两点重合于
两点重合于 ,连接
,连接 ,
, .
.
(Ⅰ)求证:
 ;
;(Ⅱ)试判断
 与平面
与平面 的位置关系,并给出证明.
的位置关系,并给出证明.
您最近一年使用:0次
2018-07-16更新
|
705次组卷
|
3卷引用:【全国市级联考】四川省攀枝花市2017-2018学年高二下学期期末调研检测数学(理)试题
名校
8 . 用反证法证明命题①:“已知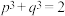 ,求证:
,求证: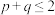 ”时,可假设“
”时,可假设“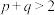 ”;命题②:“若
”;命题②:“若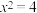 ,则
,则 或
或 ”时,可假设“
”时,可假设“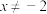 或
或 ”.以下结论正确的是
”.以下结论正确的是
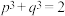 ,求证:
,求证: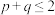 ”时,可假设“
”时,可假设“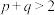 ”;命题②:“若
”;命题②:“若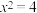 ,则
,则 或
或 ”时,可假设“
”时,可假设“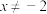 或
或 ”.以下结论正确的是
”.以下结论正确的是| A.①与②的假设都错误 | B.①与②的假设都正确 |
| C.①的假设正确,②的假设错误 | D.①的假设错误,②的假设正确 |
您最近一年使用:0次
2018-07-12更新
|
768次组卷
|
9卷引用:四川省仁寿第一中学校北校区2020-2021学年高二6月期末数学(文)试题
四川省仁寿第一中学校北校区2020-2021学年高二6月期末数学(文)试题【全国市级联考】福建省三明市2017-2018学年高二下学期期末考试数学(文)试题湖北省咸宁市2018-2019学年高二下学期期末数学(文)试题安徽省宣城市郎溪中学2020-2021学年高二下学期第一次月考理科数学试题广西河池市九校2020-2021学年高二下学期第二次联考数学(理)试题河南省灵宝市第五高级中学2021-2022学年高二下学期第一次月考数学文科试题黑龙江省大庆实验中学2021届高三得分训练(二)数学(理)试题(已下线)考点43 直接证明与间接证明-备战2022年高考数学(理)一轮复习考点微专题(已下线)数学(上海B卷)
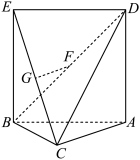
9 . 如图,在三棱柱ABC−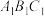 中,
中, 平面ABC,D,E,F,G分别为
平面ABC,D,E,F,G分别为 ,AC,
,AC, ,
, 的中点,AB=BC=
的中点,AB=BC= ,AC=
,AC= =2.
=2.
(2)求二面角B−CD−C1的余弦值;
(3)证明:直线FG与平面BCD相交.
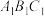 中,
中, 平面ABC,D,E,F,G分别为
平面ABC,D,E,F,G分别为 ,AC,
,AC, ,
, 的中点,AB=BC=
的中点,AB=BC= ,AC=
,AC= =2.
=2.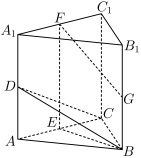
(2)求二面角B−CD−C1的余弦值;
(3)证明:直线FG与平面BCD相交.
您最近一年使用:0次
2018-06-09更新
|
15375次组卷
|
35卷引用:四川省棠湖中学2018-2019学年高二上学期期末考试数学(理)试题
四川省棠湖中学2018-2019学年高二上学期期末考试数学(理)试题四川省成都市双流区棠湖中学2018-2019学年高二上学期期末数学(理)试题【全国百强校】江西省南昌市第十中学2017-2018学年高二下学期期末考试数学(理)试题【全国百强校】山西省祁县中学2018-2019学年高二上学期期末模拟一考试数学(理)试题江苏省徐州市侯集高级中学2019-2020学年高二上学期期末数学试题山西省山西大学附中2019-2020学年高二(12月份)第四次诊断数学(理科)试题北京市第四十三中学2020-2021学年高二下学期第一次月考数学试题福建省泉州科技中学2021-2022学年高二上学期第一次月考数学试题北京市昌平区第一中学2021-2022学年高二上学期期中考试数学试题北京市景山学校2021-2022学年高二上学期期中考试数学试题辽宁省沈阳市五校协作体2021-2022学年高二上学期期中数学试题云南省大理白族自治州民族中学2023-2024学年高二下学期5月期中数学试题2018年全国普通高等学校招生统一考试理科数学(北京卷)(已下线)2018年高考题及模拟题汇编 【理科】5.立体几何北京市2019届高三数学理一轮复习典型题专项训练:立体几何(已下线)专题8.6 空间向量及空间位置关系(练)【理】-《2020年高考一轮复习讲练测》(已下线)专题8.6 空间向量及空间位置关系(讲)【理】-《2020年高考一轮复习讲练测》2020届北京市昌平区新学道临川学校高三上学期第三次月考数学(理)试题2020届北京市昌平区新学道临川学校高三上学期第三次月考数学(文)试题(已下线)专题06 立体几何(解答题)——三年(2018-2020)高考真题理科数学分项汇编(已下线)专题17 立体几何综合-五年(2016-2020)高考数学(理)真题分项(已下线)专题8.6 空间向量及其运算和空间位置关系(精讲)--2021年高考数学(理)一轮复习讲练测(已下线)专题8.6 空间向量及其运算和空间位置关系(精讲)-2021年高考数学(理)一轮复习学与练(已下线)专题4.4 空间向量与立体几何-2021年高考数学解答题挑战满分专项训练(新高考地区专用)云南省昭通市昭阳第一中学2020-2021学年高一12月月考数学(理)试题(已下线)专题10 立体几何-五年(2017-2021)高考数学真题分项(新高考地区专用)(已下线)第37讲 立体几何中的向量方法 (讲) — 2022年高考数学一轮复习讲练测(课标全国版)北京市第九中学2022届高三12月统练(月考)数学试题(已下线)专题8.7 立体几何中的向量方法(练)【理】-《2020年高考一轮复习讲练测》(已下线)专题24 空间向量与空间角的计算-十年(2011-2020)高考真题数学分项(已下线)重组卷03北京外国语大学附属中学2022届高三模拟数学试题北京十年真题专题07立体几何与空间向量北京市第一零一中学2023-2024学年高三上学期数学统练五专题09立体几何与空间向量(第二部分)
名校
10 . 如图所示, 是边长为3的正方形,
是边长为3的正方形, 平面
平面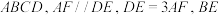 与平面
与平面 所成角为
所成角为 .
.
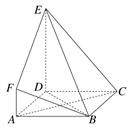
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)设点 是线段
是线段 上一个动点,试确定点
上一个动点,试确定点 的位置,使得
的位置,使得 平面
平面 ,并证明你的结论.
,并证明你的结论.
 是边长为3的正方形,
是边长为3的正方形, 平面
平面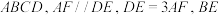 与平面
与平面 所成角为
所成角为 .
.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)设点
 是线段
是线段 上一个动点,试确定点
上一个动点,试确定点 的位置,使得
的位置,使得 平面
平面 ,并证明你的结论.
,并证明你的结论.
您最近一年使用:0次
2017-05-18更新
|
652次组卷
|
3卷引用:四川省广安市2018-2019学年高二下学期期末数学(理)试题



