1 . 约数,又称因数.它的定义如下:若整数 除以整数
除以整数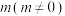 除得的商正好是整数而没有余数,我们就称
除得的商正好是整数而没有余数,我们就称 为
为 的倍数,称
的倍数,称 为
为 的约数.设正整数
的约数.设正整数 共有
共有 个正约数,即为
个正约数,即为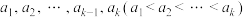 .
.
(1)当 时,若正整数
时,若正整数 的
的 个正约数构成等比数列,请写出一个
个正约数构成等比数列,请写出一个 的值;
的值;
(2)当 时,若
时,若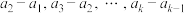 构成等比数列,求正整数
构成等比数列,求正整数 ;
;
(3)记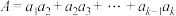 ,求证:
,求证: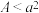 .
.
 除以整数
除以整数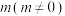 除得的商正好是整数而没有余数,我们就称
除得的商正好是整数而没有余数,我们就称 为
为 的倍数,称
的倍数,称 为
为 的约数.设正整数
的约数.设正整数 共有
共有 个正约数,即为
个正约数,即为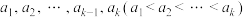 .
.(1)当
 时,若正整数
时,若正整数 的
的 个正约数构成等比数列,请写出一个
个正约数构成等比数列,请写出一个 的值;
的值;(2)当
 时,若
时,若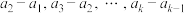 构成等比数列,求正整数
构成等比数列,求正整数 ;
;(3)记
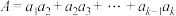 ,求证:
,求证: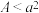 .
.
您最近一年使用:0次
2024-08-30更新
|
407次组卷
|
17卷引用:专题06 数列
(已下线)专题06 数列(已下线)高考数学冲刺押题卷02(2024新题型)(已下线)微考点4-1 新高考新试卷结构压轴题新定义数列试题分类汇编(已下线)第18题 数列与集合结合的新定义问题(高三备考9月刊)(已下线)重难点突破04 初等数论与平面几何背景下新定义(六大题型)(已下线)第四节 数列的求和【同步课时】(高三一轮北京专版)北京市通州区2023届高三上学期期末数学试题北京市第五十五中学2024届高三上学期10月月考数学试题北京市东城区第六十五中学2024届高三上学期12月月考数学试题湖南省长沙市雅礼中学2024届高三一模数学试卷(已下线)第四套 艺体生新高考全真模拟 (一模重组卷)湖南省常德市第一中学2023-2024学年高二下学期第一次月考数学试题北京市西城区北京师范大学第二附属中学2023-2024学年高二下学期期中考试数学试题(已下线)高二下学期第三次月考模拟卷(新题型)(范围:导数+选择性必修第三册)-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)广东省广州市广东实验中学2023-2024学年高三下学期教学情况测试(二)数学试卷A广东省佛山市高明区第一中学2023-2024学年高二下学期第一次大考数学试题福建省宁德市古田县第一中学2024-2025学年高三第一次模拟考试数学试卷
名校
2 . 如图,在平行六面体 中,
中,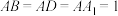 ,
, ,
,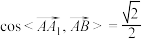 ,
, ,点
,点 为
为 中点.
中点.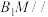 平面
平面 ;
;
(2)求二面角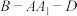 的正弦值.
的正弦值.
 中,
中,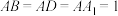 ,
, ,
,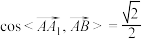 ,
, ,点
,点 为
为 中点.
中点.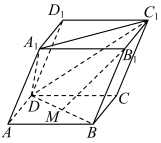
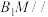 平面
平面 ;
;(2)求二面角
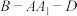 的正弦值.
的正弦值.
您最近一年使用:0次
2024-03-12更新
|
3521次组卷
|
11卷引用:专题04 立体几何
(已下线)专题04 立体几何(已下线)【一题多解】立体几何 新旧呼应(已下线)湖南省长沙市四县区2024届高三下学期3月调研考试数学试题变式题11-15(已下线)重难点突破03 立体几何解答题常考模型归纳总结(九大题型)-2辽宁省沈阳市五校联考2024届高三上学期期末数学试题(已下线)每日一题 第16题 不易建系 先证垂直(高三)湖南省长沙市雅礼中学2024届高三一模数学试卷江苏省常州市第一中学2024届高三下学期期初检测数学试题江西省宜春市丰城市第九中学2024届高三上学期期末考试数学试题辽宁省辽东十一所重点高中联合教研体2024届高三下学期高考适应性考试(一)数学试题江苏省南通市启东中学2024届高三下学期(普通班)2月考试数学试题
名校
3 . 已知函数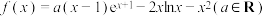 .
.
(1)当 时,求函数
时,求函数 在区间
在区间 上的最小值;
上的最小值;
(2)讨论函数 的极值点个数;
的极值点个数;
(3)当函数 无极值点时,求证:
无极值点时,求证: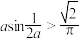 .
.
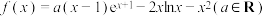 .
.(1)当
 时,求函数
时,求函数 在区间
在区间 上的最小值;
上的最小值;(2)讨论函数
 的极值点个数;
的极值点个数;(3)当函数
 无极值点时,求证:
无极值点时,求证: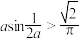 .
.
您最近一年使用:0次
2024-02-29更新
|
4085次组卷
|
5卷引用:信息必刷卷04
名校
解题方法
4 . 在某数字通信中,信号的传输包含发送与接收两个环节.每次信号只发送0和1中的某个数字,由于随机因素干扰,接收到的信号数字有可能出现错误,已知发送信号0时,接收为0和1的概率分别为 ,
, ;发送信号1时,接收为1和0的概率分别为
;发送信号1时,接收为1和0的概率分别为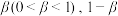 .假设每次信号的传输相互独立.
.假设每次信号的传输相互独立.
(1)当连续三次发送信号均为0时,设其相应三次接收到的信号数字均相同的概率为 ,求
,求 的最小值;
的最小值;
(2)当连续四次发送信号均为1时,设其相应四次接收到的信号数字依次为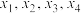 ,记其中连续出现相同数字的次数的最大值为随机变量
,记其中连续出现相同数字的次数的最大值为随机变量 (
(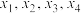 中任意相邻的数字均不相同时,令
中任意相邻的数字均不相同时,令 ),若
),若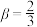 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
 ,
, ;发送信号1时,接收为1和0的概率分别为
;发送信号1时,接收为1和0的概率分别为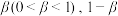 .假设每次信号的传输相互独立.
.假设每次信号的传输相互独立.(1)当连续三次发送信号均为0时,设其相应三次接收到的信号数字均相同的概率为
 ,求
,求 的最小值;
的最小值;(2)当连续四次发送信号均为1时,设其相应四次接收到的信号数字依次为
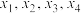 ,记其中连续出现相同数字的次数的最大值为随机变量
,记其中连续出现相同数字的次数的最大值为随机变量 (
(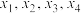 中任意相邻的数字均不相同时,令
中任意相邻的数字均不相同时,令 ),若
),若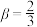 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
您最近一年使用:0次
2024-02-29更新
|
6188次组卷
|
8卷引用:信息必刷卷04
(已下线)信息必刷卷04广东省深圳市2024届高三第一次调研考试数学试卷湖北省黄冈市浠水县第一中学2024届高三下学期第一次高考模拟数学试题(已下线)山东省部分学校2024届高三3月调研数学试卷(2024年普通高等学校招生全国统一考试数学模拟试卷)江苏省连云港市连云港高级中学2023-2024学年高三下学期4月阶段测试数学试题江苏省淮安市洪泽中学,金湖中学,清河中学,清浦中学等学校2023-2024学年高二下学期5月月考数学试题江苏省常州市第一中学2023-2024学年高二下学期6月阶段检测数学试题吉林省长春市第二中学2025届高三上学期第二次调研考试数学试题
名校
解题方法
5 . 记 的内角
的内角 的对边分别为
的对边分别为 ,已知
,已知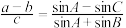 .
.
(1)求角 的大小;
的大小;
(2)若 ,求
,求 周长的最大值.
周长的最大值.
 的内角
的内角 的对边分别为
的对边分别为 ,已知
,已知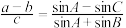 .
.(1)求角
 的大小;
的大小;(2)若
 ,求
,求 周长的最大值.
周长的最大值.
您最近一年使用:0次
2024-02-24更新
|
4197次组卷
|
5卷引用:专题05 三角函数
(已下线)专题05 三角函数(已下线)专题11.2正弦定理-重难点突破及混淆易错规避(苏教版2019必修第二册)广西壮族自治区南宁市第三中学、柳州高级中学2024届高三下学期一轮复习诊断性联考数学试卷黑龙江省牡丹江市第一高级中学2023-2024学年高一下学期4月月考数学试题四川省巴中市平昌中学2023-2024学年高一下学期第一次月考数学试题
名校
解题方法
6 . 已知曲线 .
.
(1)若点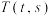 是
是 上的任意一点,直线
上的任意一点,直线 ,判断直线
,判断直线 与
与 的位置关系并证明.
的位置关系并证明.
(2)若 是直线
是直线 上的动点,直线
上的动点,直线 与
与 相切于点
相切于点 ,直线
,直线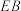 与
与 相切于点
相切于点 .
.
①试问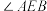 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
②若直线 与
与 轴分别交于点
轴分别交于点 ,证明:
,证明: .
.
 .
.(1)若点
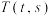 是
是 上的任意一点,直线
上的任意一点,直线 ,判断直线
,判断直线 与
与 的位置关系并证明.
的位置关系并证明.(2)若
 是直线
是直线 上的动点,直线
上的动点,直线 与
与 相切于点
相切于点 ,直线
,直线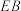 与
与 相切于点
相切于点 .
.①试问
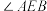 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.②若直线
 与
与 轴分别交于点
轴分别交于点 ,证明:
,证明: .
.
您最近一年使用:0次
名校
7 . 在如图所示的五面体 中,
中,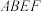 共面,
共面,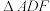 是正三角形,四边形
是正三角形,四边形 为菱形,
为菱形,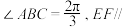 平面
平面 ,点
,点 为
为 中点.
中点.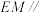 平面
平面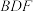 ;
;
(2)已知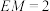 ,求平面
,求平面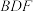 与平面
与平面 所成二面角的正弦值.
所成二面角的正弦值.
 中,
中,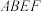 共面,
共面,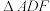 是正三角形,四边形
是正三角形,四边形 为菱形,
为菱形,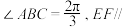 平面
平面 ,点
,点 为
为 中点.
中点.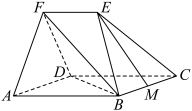
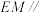 平面
平面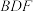 ;
;(2)已知
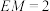 ,求平面
,求平面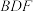 与平面
与平面 所成二面角的正弦值.
所成二面角的正弦值.
您最近一年使用:0次
2024-02-24更新
|
2383次组卷
|
4卷引用:专题04 立体几何
名校
8 . 某校为了丰富学生课余生活,体育节组织定点投篮比赛.为了解学生喜欢篮球是否与性别有关,随机抽取了男、女同学各100名进行调查,部分数据如表所示:
(1)根据所给数据完成上表,依据小概率值 的
的 独立性检验,能否据此推断该校学生喜欢篮球与性别有关?
独立性检验,能否据此推断该校学生喜欢篮球与性别有关?
(2)篮球指导老师从喜欢篮球的学生中抽取了2名男生和1名女生进行投篮示范.已知这两名男生投进的概率均为 ,这名女生投进的概率为
,这名女生投进的概率为 ,每人投篮一次,假设各人投篮相互独立,求3人投进总次数
,每人投篮一次,假设各人投篮相互独立,求3人投进总次数 的分布列和数学期望.
的分布列和数学期望.
附:
喜欢篮球 | 不喜欢篮球 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 |
 的
的 独立性检验,能否据此推断该校学生喜欢篮球与性别有关?
独立性检验,能否据此推断该校学生喜欢篮球与性别有关?(2)篮球指导老师从喜欢篮球的学生中抽取了2名男生和1名女生进行投篮示范.已知这两名男生投进的概率均为
 ,这名女生投进的概率为
,这名女生投进的概率为 ,每人投篮一次,假设各人投篮相互独立,求3人投进总次数
,每人投篮一次,假设各人投篮相互独立,求3人投进总次数 的分布列和数学期望.
的分布列和数学期望.附:

| 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2024-02-24更新
|
2109次组卷
|
6卷引用:专题08 平面向量、概率、统计、计数原理
(已下线)专题08 平面向量、概率、统计、计数原理(已下线)【一题多变】 分类变量 独立检验河北省保定市高碑店市崇德实验中学2024届高三下学期3月月考数学试题(已下线)专题8.4 统计分析大题专项训练【六大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)广西壮族自治区南宁市第三中学、柳州高级中学2024届高三下学期一轮复习诊断性联考数学试卷2024届河南省驻马店市经开区高考三模数学试卷
名校
解题方法
9 . 在平面直角坐标系 中,点
中,点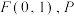 为动点,以
为动点,以 为直径的圆与
为直径的圆与 轴相切,记
轴相切,记 的轨迹为
的轨迹为 .
.
(1)求 的方程;
的方程;
(2)设 为直线
为直线 上的动点,过
上的动点,过 的直线与
的直线与 相切于点
相切于点 ,过
,过 作直线
作直线 的垂线交
的垂线交 于点
于点 ,求
,求 面积的最小值.
面积的最小值.
 中,点
中,点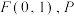 为动点,以
为动点,以 为直径的圆与
为直径的圆与 轴相切,记
轴相切,记 的轨迹为
的轨迹为 .
.(1)求
 的方程;
的方程;(2)设
 为直线
为直线 上的动点,过
上的动点,过 的直线与
的直线与 相切于点
相切于点 ,过
,过 作直线
作直线 的垂线交
的垂线交 于点
于点 ,求
,求 面积的最小值.
面积的最小值.
您最近一年使用:0次
2024-02-24更新
|
2413次组卷
|
7卷引用:专题07 直线与圆、圆锥曲线
(已下线)专题07 直线与圆、圆锥曲线(已下线)信息必刷卷05(已下线)第四套 最新模拟复盘卷(已下线)信息必刷卷04(江苏专用,2024新题型)黑龙江省齐齐哈尔市2024届高三第一次模拟考试数学试题山西省怀仁市第一中学校2023-2024学年高三下学期第三次模拟考试数学试题江苏省盐城市2023-2024学年高二下学期5月月考数学试题
名校
10 . 已知函数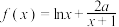 .
.
(1)设函数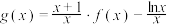 ,讨论
,讨论 的单调性;
的单调性;
(2)设 分别为
分别为 的极大值点和极小值点,证明:
的极大值点和极小值点,证明: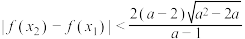 .
.
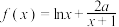 .
.(1)设函数
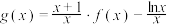 ,讨论
,讨论 的单调性;
的单调性;(2)设
 分别为
分别为 的极大值点和极小值点,证明:
的极大值点和极小值点,证明: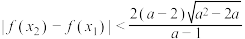 .
.
您最近一年使用:0次
2024-02-24更新
|
1770次组卷
|
6卷引用:专题03 函数的概念与性质(含导数)
(已下线)专题03 函数的概念与性质(含导数)(已下线)模块2专题7 对数均值不等式 巧妙解决双变量练黑龙江省齐齐哈尔市2024届高三第一次模拟考试数学试题吉林省通化市三区九校2023-2024学年高二下学期7月期末考试数学试题陕西省宝鸡市千阳县中学2023-2024学年高二下学期期末考试数学试题山西省朔州市怀仁市第一中学校2025届高三上学期10月月考数学试题





