1 . 若有限集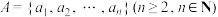 ,且满足
,且满足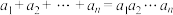 ,则称A为“完美集”.
,则称A为“完美集”.
(1)若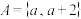 为“完美集”,则实数
为“完美集”,则实数
______ :
(2)若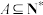 且为“完美集”,则
且为“完美集”,则
______ .
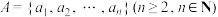 ,且满足
,且满足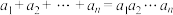 ,则称A为“完美集”.
,则称A为“完美集”.(1)若
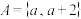 为“完美集”,则实数
为“完美集”,则实数
(2)若
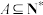 且为“完美集”,则
且为“完美集”,则
您最近一年使用:0次
2 . 给定集合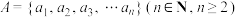 ,定义
,定义 中所有不同值的个数为集合
中所有不同值的个数为集合 两个元素的容量,用
两个元素的容量,用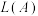 表示.
表示.
①若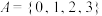 ,则
,则
___________ ;
②定义函数 其中
其中 表示不超过
表示不超过 的最大整数,如
的最大整数,如 ,
,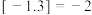 ,当
,当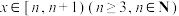 时,函数
时,函数 的值域为
的值域为 ,若
,若 ,则
,则
____________ ;
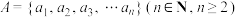 ,定义
,定义 中所有不同值的个数为集合
中所有不同值的个数为集合 两个元素的容量,用
两个元素的容量,用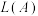 表示.
表示.①若
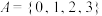 ,则
,则
②定义函数
 其中
其中 表示不超过
表示不超过 的最大整数,如
的最大整数,如 ,
,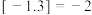 ,当
,当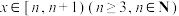 时,函数
时,函数 的值域为
的值域为 ,若
,若 ,则
,则
您最近一年使用:0次
2024-06-12更新
|
640次组卷
|
4卷引用:山西省运城市康杰中学2023-2024学年高三第十九次大型考试数学仿真训练试题
山西省运城市康杰中学2023-2024学年高三第十九次大型考试数学仿真训练试题辽宁省沈阳市第二中学2025届高三上学期期初考试数学试卷(已下线)第1讲 集合中的思想方法--数学思想方法(同步)【练】山东省枣庄市滕州市2024-2025学年高三上学期11月定时训练(期中)数学试题
名校
3 . 记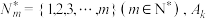 表示k个元素的有限集,
表示k个元素的有限集,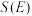 表示非空数集E中所有元素的和,若集合
表示非空数集E中所有元素的和,若集合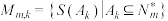 ,则
,则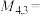
_____ ,若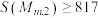 ,则m的最小值为
,则m的最小值为_____ .
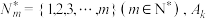 表示k个元素的有限集,
表示k个元素的有限集,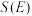 表示非空数集E中所有元素的和,若集合
表示非空数集E中所有元素的和,若集合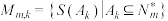 ,则
,则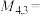
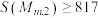 ,则m的最小值为
,则m的最小值为
您最近一年使用:0次
2024-05-04更新
|
1054次组卷
|
6卷引用:福建省三明市2024届普通高中高三毕业班质量检测数学试题
福建省三明市2024届普通高中高三毕业班质量检测数学试题江苏省扬州中学2024届高三下学期全真模拟数学试卷(已下线)考点1 集合 --高考数学100个黄金考点(2025届)【练】(已下线)考点01 集合 --高考数学100个黄金考点(2025届)1【练】江苏省扬州中学2024-2025学年高三上学期暑期检测数学试题江苏省徐州市第七中学2025届高三上学期开学考试(9月)数学试题
4 . 设 是正整数,集合
是正整数,集合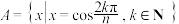 .当
.当 ,集合
,集合 有
有______ 个元素;若集合 有100个元素,则
有100个元素,则
______ .
 是正整数,集合
是正整数,集合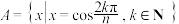 .当
.当 ,集合
,集合 有
有 有100个元素,则
有100个元素,则
您最近一年使用:0次
名校
解题方法
5 . 设集合 为满足
为满足 ,
, ,
, 的空间向量
的空间向量 ,
, ,
, 中可能出现的两两共线的向量组数组成的数集,集合
中可能出现的两两共线的向量组数组成的数集,集合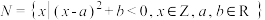 ,若
,若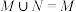 ,则
,则 的取值范围为
的取值范围为______ ,当 最小时,
最小时, 的取值为
的取值为______ .
 为满足
为满足 ,
, ,
, 的空间向量
的空间向量 ,
, ,
, 中可能出现的两两共线的向量组数组成的数集,集合
中可能出现的两两共线的向量组数组成的数集,集合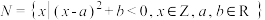 ,若
,若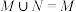 ,则
,则 的取值范围为
的取值范围为 最小时,
最小时, 的取值为
的取值为
您最近一年使用:0次
2024-02-21更新
|
654次组卷
|
2卷引用:广东省广州市华南师范大学附属中学2024届高三上学期数学周测试题(12)
名校
解题方法
6 . 函数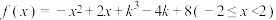 的最大值记为M,最小值记为m,其中
的最大值记为M,最小值记为m,其中 为负常数,若
为负常数,若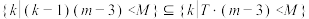 ,则
,则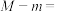
您最近一年使用:0次
2023-10-30更新
|
644次组卷
|
3卷引用:第1题 集合关系与运算,转化化归渡难关
7 . 给定集合 ,定义
,定义 中所有不同值的个数为集合A两个元素的容量,用
中所有不同值的个数为集合A两个元素的容量,用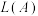 表示.
表示.
①若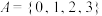 ,则
,则
________ ;
②定义函数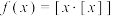 其中
其中 表示不超过x的最大整数,如
表示不超过x的最大整数,如 ,
,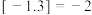 ,当
,当 时,函数
时,函数 的值域为A,若
的值域为A,若 ,则
,则
________ ;
 ,定义
,定义 中所有不同值的个数为集合A两个元素的容量,用
中所有不同值的个数为集合A两个元素的容量,用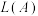 表示.
表示.①若
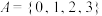 ,则
,则
②定义函数
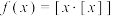 其中
其中 表示不超过x的最大整数,如
表示不超过x的最大整数,如 ,
,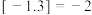 ,当
,当 时,函数
时,函数 的值域为A,若
的值域为A,若 ,则
,则
您最近一年使用:0次
8 . 记函数 (
( )的最小正周期为T,给出下列三个命题:
)的最小正周期为T,给出下列三个命题:
甲: ;
;
乙: 在区间
在区间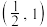 上单调递减;
上单调递减;
丙: 在区间
在区间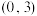 上恰有三个极值点.
上恰有三个极值点.
若这三个命题中有且仅有一个假命题,则假命题是________ (填“甲”、“已”或“丙”); 的取值范围是
的取值范围是________ .
 (
( )的最小正周期为T,给出下列三个命题:
)的最小正周期为T,给出下列三个命题:甲:
 ;
;乙:
 在区间
在区间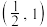 上单调递减;
上单调递减;丙:
 在区间
在区间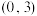 上恰有三个极值点.
上恰有三个极值点.若这三个命题中有且仅有一个假命题,则假命题是
 的取值范围是
的取值范围是
您最近一年使用:0次
名校
9 . 对于平面上的两个点 ,
, ,若满足①
,若满足① ,②
,② ,③前面两个不等式中至少有一个“
,③前面两个不等式中至少有一个“ ”不成立,则称
”不成立,则称 是相对于
是相对于 的一个优先点,记作“
的一个优先点,记作“ ”. 已知点集
”. 已知点集 .
.
(Ⅰ)若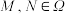 ,
, ,则可以构成
,则可以构成_____ 组优先点;
(Ⅱ)若点集 ,且集合
,且集合 中的任意两个点都不能构成一组优先点,则集合
中的任意两个点都不能构成一组优先点,则集合 中的元素最多可以有
中的元素最多可以有_____ 个.
 ,
, ,若满足①
,若满足① ,②
,② ,③前面两个不等式中至少有一个“
,③前面两个不等式中至少有一个“ ”不成立,则称
”不成立,则称 是相对于
是相对于 的一个优先点,记作“
的一个优先点,记作“ ”. 已知点集
”. 已知点集 .
.(Ⅰ)若
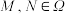 ,
, ,则可以构成
,则可以构成(Ⅱ)若点集
 ,且集合
,且集合 中的任意两个点都不能构成一组优先点,则集合
中的任意两个点都不能构成一组优先点,则集合 中的元素最多可以有
中的元素最多可以有
您最近一年使用:0次
2021-09-25更新
|
472次组卷
|
2卷引用:北京市第十三中学2022届高三上学期开学考数学试题
解题方法
10 . 关于下列两个命题:设 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, 单调,则方程
单调,则方程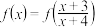 的所有根之和为
的所有根之和为______ ;对于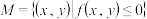 有性质
有性质 :“对
:“对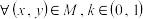 时,必有
时,必有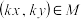 .现给定①
.现给定①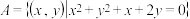 ;②
;②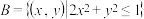 ;现与
;现与 对比,①中
对比,①中 、②中
、②中 同样也有性质
同样也有性质 的序号为
的序号为______ .
 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, 单调,则方程
单调,则方程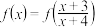 的所有根之和为
的所有根之和为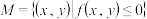 有性质
有性质 :“对
:“对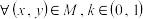 时,必有
时,必有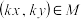 .现给定①
.现给定①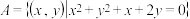 ;②
;②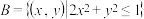 ;现与
;现与 对比,①中
对比,①中 、②中
、②中 同样也有性质
同样也有性质 的序号为
的序号为
您最近一年使用:0次



