解题方法
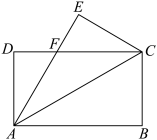
1 . 如图,矩形 的周长为定值
的周长为定值 ,把
,把 沿
沿 翻折,
翻折, 折过去后交
折过去后交 边于点
边于点 ,设
,设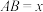 .
.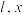 表示
表示 ,并求
,并求 的取值范围;
的取值范围;
(2)设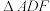 的面积为
的面积为 ,求
,求 关于
关于 的函数表达式及
的函数表达式及 的最大值.
的最大值.
 的周长为定值
的周长为定值 ,把
,把 沿
沿 翻折,
翻折, 折过去后交
折过去后交 边于点
边于点 ,设
,设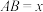 .
.
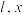 表示
表示 ,并求
,并求 的取值范围;
的取值范围;(2)设
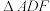 的面积为
的面积为 ,求
,求 关于
关于 的函数表达式及
的函数表达式及 的最大值.
的最大值.
您最近一年使用:0次
名校
2 . 已知函数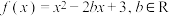 .
.
(1)若函数 的图象经过点
的图象经过点 ,求实数
,求实数 的值;
的值;
(2)在(1)的条件下,求不等式 的解集;
的解集;
(3)解关于 的不等式
的不等式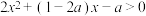 .
.
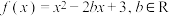 .
.(1)若函数
 的图象经过点
的图象经过点 ,求实数
,求实数 的值;
的值;(2)在(1)的条件下,求不等式
 的解集;
的解集;(3)解关于
 的不等式
的不等式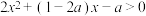 .
.
您最近一年使用:0次
7日内更新
|
493次组卷
|
3卷引用:四川省成都市温江区东辰外国语学校2024-2025学年高一上学期第一学程测试数学试卷mm
解题方法
3 . 经研究,函数 为奇函数的充要条件是函数
为奇函数的充要条件是函数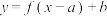 图象的对称中心为点
图象的对称中心为点 ,函数
,函数 的图象关于点
的图象关于点 成中心对称图形的充要条件是函数
成中心对称图形的充要条件是函数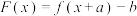 为奇函数,由
为奇函数,由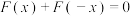 得函数
得函数 关于点
关于点 成中心对称图形的充要条件是
成中心对称图形的充要条件是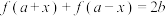 .
.
(1)已知函数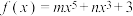 ,且
,且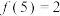 ,求
,求 的值;
的值;
(2)证明函数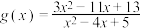 图象的对称中心为
图象的对称中心为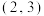 ;
;
(3)已知函数 ,求
,求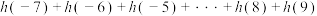 的值.
的值.
 为奇函数的充要条件是函数
为奇函数的充要条件是函数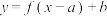 图象的对称中心为点
图象的对称中心为点 ,函数
,函数 的图象关于点
的图象关于点 成中心对称图形的充要条件是函数
成中心对称图形的充要条件是函数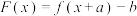 为奇函数,由
为奇函数,由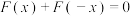 得函数
得函数 关于点
关于点 成中心对称图形的充要条件是
成中心对称图形的充要条件是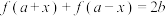 .
.(1)已知函数
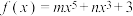 ,且
,且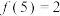 ,求
,求 的值;
的值;(2)证明函数
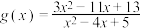 图象的对称中心为
图象的对称中心为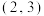 ;
;(3)已知函数
 ,求
,求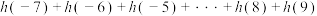 的值.
的值.
您最近一年使用:0次
7日内更新
|
167次组卷
|
2卷引用:四川省成都市九县区2024-2025学年高一上学期期中考试数学试题
名校
解题方法
4 . 定义在 上的函数
上的函数 满足:①对
满足:①对 ,有
,有 成立; ②
成立; ②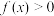 ;③当
;③当 时,有
时,有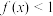 ;④
;④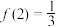 .
.
(1)计算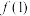 ,
,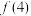 ,
,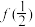 ,
,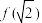 ,
,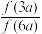 的值;
的值;
(2)证明:(i)当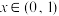 时,
时,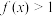 ,
,
(ii) 是减函数;
是减函数;
(3)设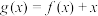 ,记
,记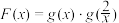 ,求
,求 的最小值.
的最小值.
 上的函数
上的函数 满足:①对
满足:①对 ,有
,有 成立; ②
成立; ②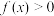 ;③当
;③当 时,有
时,有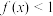 ;④
;④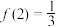 .
.(1)计算
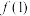 ,
,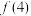 ,
,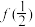 ,
,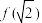 ,
,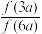 的值;
的值;(2)证明:(i)当
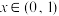 时,
时,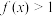 ,
,(ii)
 是减函数;
是减函数;(3)设
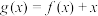 ,记
,记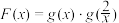 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
名校
解题方法
5 . 已知函数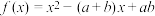 .
.
(1)若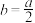 , 讨论关于
, 讨论关于 的不等式
的不等式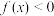 的解集(用
的解集(用 表示);
表示);
(2)若 , 当
, 当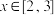 时,
时, 图象恒在
图象恒在 图象的上方,求
图象的上方,求 的取值范围.
的取值范围.
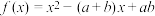 .
.(1)若
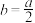 , 讨论关于
, 讨论关于 的不等式
的不等式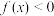 的解集(用
的解集(用 表示);
表示);(2)若
 , 当
, 当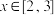 时,
时, 图象恒在
图象恒在 图象的上方,求
图象的上方,求 的取值范围.
的取值范围.
您最近一年使用:0次
名校
6 . 已知函数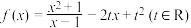 .
.
(1)设集合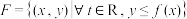 ,判断
,判断 是否是
是否是 中的元素,并说明理由;
中的元素,并说明理由;
(2)证明:当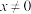 时,
时,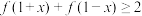 ;
;
(3)当 时,若有方程
时,若有方程 的两相异实根均在
的两相异实根均在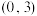 内,求
内,求 的取值范围.
的取值范围.
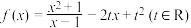 .
.(1)设集合
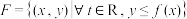 ,判断
,判断 是否是
是否是 中的元素,并说明理由;
中的元素,并说明理由;(2)证明:当
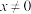 时,
时,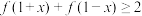 ;
;(3)当
 时,若有方程
时,若有方程 的两相异实根均在
的两相异实根均在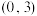 内,求
内,求 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
7 . 奇函数 定义域为
定义域为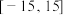 ,当
,当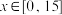 时,
时,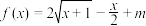 .
.
(1)求 的值,并给出当
的值,并给出当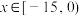 时
时 的解析式;
的解析式;
(2)求函数 的值域.
的值域.
 定义域为
定义域为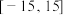 ,当
,当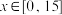 时,
时,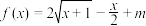 .
.(1)求
 的值,并给出当
的值,并给出当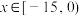 时
时 的解析式;
的解析式;(2)求函数
 的值域.
的值域.
您最近一年使用:0次
解题方法
8 . 定义在 上的函数
上的函数 满足:对任意
满足:对任意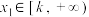 ,都存在唯一
,都存在唯一 ,使得
,使得 ,则称函数
,则称函数 是“
是“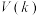 型函数”(其中
型函数”(其中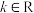 ).
).
(1)判断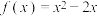 是否为“
是否为“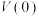 型函数”?并说明理由;
型函数”?并说明理由;
(2)是否存在实数 ,使得函数
,使得函数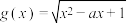 是“
是“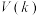 型函数”,若存在,求出
型函数”,若存在,求出 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(3)若函数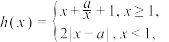 是“
是“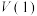 型函数”,求实数
型函数”,求实数 的取值范围.
的取值范围.
 上的函数
上的函数 满足:对任意
满足:对任意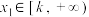 ,都存在唯一
,都存在唯一 ,使得
,使得 ,则称函数
,则称函数 是“
是“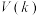 型函数”(其中
型函数”(其中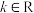 ).
).(1)判断
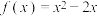 是否为“
是否为“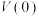 型函数”?并说明理由;
型函数”?并说明理由;(2)是否存在实数
 ,使得函数
,使得函数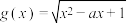 是“
是“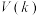 型函数”,若存在,求出
型函数”,若存在,求出 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;(3)若函数
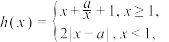 是“
是“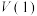 型函数”,求实数
型函数”,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
9 . 在①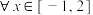 ,②
,②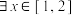 这两个条件中任选一个,补充到下面问题的横线中,并求解该问题.已知函数
这两个条件中任选一个,补充到下面问题的横线中,并求解该问题.已知函数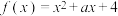 .
.
(1)当 时,求函数
时,求函数 在区间
在区间 上的最大值与最小值;
上的最大值与最小值;
(2)若__________, ,求实数
,求实数 的取值范围.
的取值范围.
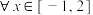 ,②
,②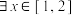 这两个条件中任选一个,补充到下面问题的横线中,并求解该问题.已知函数
这两个条件中任选一个,补充到下面问题的横线中,并求解该问题.已知函数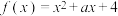 .
.(1)当
 时,求函数
时,求函数 在区间
在区间 上的最大值与最小值;
上的最大值与最小值;(2)若__________,
 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
10 . 已知函数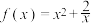 的定义域为
的定义域为 .
.
(1)根据单调性的定义,证明 在
在 上是增函数;
上是增函数;
(2)若函数 对
对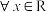 都满足
都满足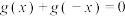 且是
且是 上的减函数,不等式
上的减函数,不等式 在
在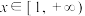 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
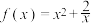 的定义域为
的定义域为 .
.(1)根据单调性的定义,证明
 在
在 上是增函数;
上是增函数;(2)若函数
 对
对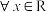 都满足
都满足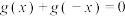 且是
且是 上的减函数,不等式
上的减函数,不等式 在
在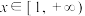 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次



