2024·全国·模拟预测
1 . 在参数估计的各种方法中极大似然估计法是应用最为广泛的一种估计方式,它广泛运用在金融、工程、生物制药等领域.把使样本事件发生概率最大的参数值,作为总体参数的估计值,就是极大似然估计.求极大似然估计的一般步骤:(1)由总体分布导出样本的联合概率函数(或联合密度);(2)把样本联合概率函数(或联合密度)中自变量看成已知常数,而把参数 看作自变量,得到似然函数
看作自变量,得到似然函数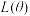 ;(3)求似然函数
;(3)求似然函数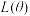 的最大值点(常转化为求对数似然函数
的最大值点(常转化为求对数似然函数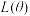 的最大值点);(4)在最大值点的表达式中,用样本值代入就得参数的极大似然估计值.已知服从正态分布
的最大值点);(4)在最大值点的表达式中,用样本值代入就得参数的极大似然估计值.已知服从正态分布 的样本中参数
的样本中参数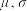 的似然函数为
的似然函数为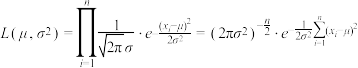 ;服从二项分布的似然函数为
;服从二项分布的似然函数为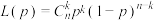 (其中
(其中 表示成功的概率,
表示成功的概率, 为样本总数,
为样本总数, 为成功次数),则下列说法正确的有( )
为成功次数),则下列说法正确的有( )
 看作自变量,得到似然函数
看作自变量,得到似然函数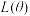 ;(3)求似然函数
;(3)求似然函数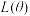 的最大值点(常转化为求对数似然函数
的最大值点(常转化为求对数似然函数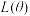 的最大值点);(4)在最大值点的表达式中,用样本值代入就得参数的极大似然估计值.已知服从正态分布
的最大值点);(4)在最大值点的表达式中,用样本值代入就得参数的极大似然估计值.已知服从正态分布 的样本中参数
的样本中参数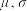 的似然函数为
的似然函数为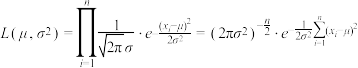 ;服从二项分布的似然函数为
;服从二项分布的似然函数为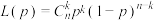 (其中
(其中 表示成功的概率,
表示成功的概率, 为样本总数,
为样本总数, 为成功次数),则下列说法正确的有( )
为成功次数),则下列说法正确的有( )A. 的极大似然估计值为 的极大似然估计值为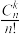 |
B.参数 的极大似然估计值为 的极大似然估计值为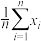 |
C.参数 的极大似然估计值为 的极大似然估计值为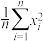 |
D.二项分布中成功的次数与不成功的次数之比的极大似然估计值为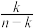 |
您最近半年使用:0次
23-24高二下·广东茂名·阶段练习
名校
2 . 已知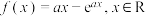 ,则( )
,则( )
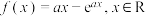 ,则( )
,则( )A. 的值域为 的值域为 |
B. 时, 时, 恒有极值点 恒有极值点 |
C.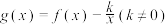 恒有零点 恒有零点 |
D.对于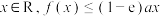 恒成立 恒成立 |
您最近半年使用:0次
2024-04-12更新
|
414次组卷
|
3卷引用:模块2 专题4 泰勒公式 巧解压轴 练
名校
3 . 关于函数 ,下列判断正确的是( ).
,下列判断正确的是( ).
 ,下列判断正确的是( ).
,下列判断正确的是( ).A. 是 是 的极大值点 的极大值点 |
B.函数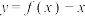 有且只有1个零点 有且只有1个零点 |
C.存在正实数 ,使得 ,使得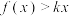 成立 成立 |
D.对任意两个正实数 ,且 ,且 ,若 ,若 ,则 ,则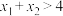 . . |
您最近半年使用:0次
名校
4 . 已知 ,函数
,函数 有两个极值点
有两个极值点 ,则( )
,则( )
 ,函数
,函数 有两个极值点
有两个极值点 ,则( )
,则( )A. |
B. 时,函数 时,函数 的图象在 的图象在 处的切线方程为 处的切线方程为 |
C. 为定值 为定值 |
D.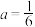 时,函数 时,函数 在 在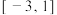 上的值域是 上的值域是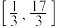 |
您最近半年使用:0次
2024-04-10更新
|
439次组卷
|
2卷引用:贵州省毕节市织金县部分学校2024届高三下学期一模考试数学试题(一)
5 . 已知 ,且
,且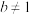 ,函数
,函数 ,其中
,其中 为自然对数的底数,则( )
为自然对数的底数,则( )
A.若该函数为偶函数,则其最小值为 |
B.函数 的图像经过唯一的定点 的图像经过唯一的定点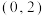 |
C.若关于 的方程 的方程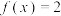 有且只有一个解,则 有且只有一个解,则 或 或 |
D.令 为 为 上的连续函数,则当 上的连续函数,则当 时 时 至多存在一个零点 至多存在一个零点 |
您最近半年使用:0次
名校
6 . 已知函数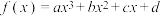 存在两个极值点
存在两个极值点 ,且
,且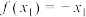 ,
, .设
.设 的零点个数为
的零点个数为 ,方程
,方程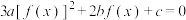 的实根个数为
的实根个数为 ,则( )
,则( )
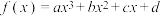 存在两个极值点
存在两个极值点 ,且
,且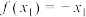 ,
, .设
.设 的零点个数为
的零点个数为 ,方程
,方程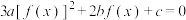 的实根个数为
的实根个数为 ,则( )
,则( )A.当 时, 时, | B.当 时, 时, |
C. 一定能被3整除 一定能被3整除 | D.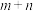 的取值集合为 的取值集合为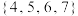 |
您最近半年使用:0次
2024-03-14更新
|
1319次组卷
|
4卷引用:湖北省八市2024届高三下学期3月联考数学试卷
湖北省八市2024届高三下学期3月联考数学试卷(已下线)第2套 全真模拟篇复盘卷 【模块三】海南省海南中学2024届高三第一次模拟数学试题江苏省连云港市东海高级中学2023-2024学年高二下学期强化班第一次月考数学试题
名校
7 . 已知函数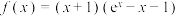 ,则下列说法正确的有
,则下列说法正确的有
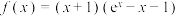 ,则下列说法正确的有
,则下列说法正确的有A. 有唯一零点 有唯一零点 |
B. 无最大值 无最大值 |
C. 在区间 在区间 上单调递增 上单调递增 |
D. 为 为 的一个极小值点 的一个极小值点 |
您最近半年使用:0次
2024-03-13更新
|
1037次组卷
|
2卷引用:湖南省长沙市雅礼中学2024届高三下学期月考(七)数学试题
名校
8 . 已知函数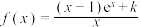 ,其导函数为
,其导函数为 ,且
,且 ,记
,记 ,则下列说法正确的是( )
,则下列说法正确的是( )
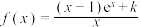 ,其导函数为
,其导函数为 ,且
,且 ,记
,记 ,则下列说法正确的是( )
,则下列说法正确的是( )A.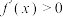 恒成立 恒成立 |
B.函数 的极小值为0 的极小值为0 |
C.若函数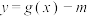 在其定义域内有两个不同的零点,则实数 在其定义域内有两个不同的零点,则实数 的取值范围是 的取值范围是 |
D.对任意的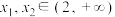 ,都有 ,都有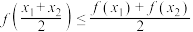 |
您最近半年使用:0次
2024-03-06更新
|
826次组卷
|
4卷引用:山西省晋城市第一中学校2024届高三下学期第十四次调研考试数学试题
9 . 若过点 可作曲线
可作曲线 的n条切线
的n条切线 ,则( )
,则( )
 可作曲线
可作曲线 的n条切线
的n条切线 ,则( )
,则( )A.若 ,则 ,则 |
B.若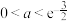 ,且 ,且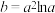 ,则 ,则 |
C.若 ,则 ,则 |
D.过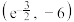 ,仅可作 ,仅可作 的一条切线 的一条切线 |
您最近半年使用:0次
10 . 已知函数 在
在 上可导且
上可导且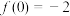 ,其导函数
,其导函数 满足:
满足: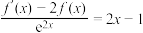 ,则下列结论正确的是( )
,则下列结论正确的是( )
 在
在 上可导且
上可导且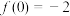 ,其导函数
,其导函数 满足:
满足: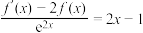 ,则下列结论正确的是( )
,则下列结论正确的是( )A.函数 有且仅有两个零点 有且仅有两个零点 |
B.函数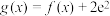 有且仅有三个零点 有且仅有三个零点 |
C.当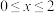 时,不等式 时,不等式 恒成立 恒成立 |
D. 在 在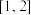 上的值域为 上的值域为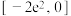 |
您最近半年使用:0次



