名校
1 . 已知 是边长为4的等边三角形,将它沿中线
是边长为4的等边三角形,将它沿中线 折起得四面体
折起得四面体 ,使得此时
,使得此时 ,则四面体
,则四面体 的外接球表面积为
的外接球表面积为_______ .
 是边长为4的等边三角形,将它沿中线
是边长为4的等边三角形,将它沿中线 折起得四面体
折起得四面体 ,使得此时
,使得此时 ,则四面体
,则四面体 的外接球表面积为
的外接球表面积为
您最近一年使用:0次
2024-07-13更新
|
221次组卷
|
2卷引用:宁夏回族自治区石嘴山市第三中学2023-2024学年高一下学期7月期末数学试题
名校
解题方法
2 . 已知 的面积为9,
的面积为9, ,过D分别作
,过D分别作 于E,
于E, 于F,且
于F,且 ,则
,则
______ .
 的面积为9,
的面积为9, ,过D分别作
,过D分别作 于E,
于E, 于F,且
于F,且 ,则
,则
您最近一年使用:0次
2024-06-13更新
|
253次组卷
|
2卷引用:宁夏石嘴山市平罗县平罗中学2023-2024学年高一下学期期末考试数学试卷
名校
解题方法
3 . 著名的费马问题是法国数学家皮埃尔·德·费马(1601-1665)于1643年提出的平面几何极值问题:“已知一个三角形,求作一点,使其与此三角形的三个顶点的距离之和最小”费马问题中的所求点称为费马点,已知对于每个给定的三角形,都存在唯一的费马点,当△ABC的三个内角均小于120°时,则使得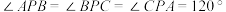 的点P即为费马点.在△ABC中,角A,B,C的对边分别为
的点P即为费马点.在△ABC中,角A,B,C的对边分别为 ,且
,且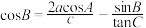 .若
.若 是
是 的“费马点”,
的“费马点”, .
.
(1)求角 ;
;
(2)若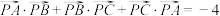 ,求
,求 的周长;
的周长;
(3)在(2)的条件下,设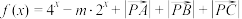 ,若当
,若当 时,不等式
时,不等式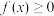 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
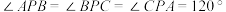 的点P即为费马点.在△ABC中,角A,B,C的对边分别为
的点P即为费马点.在△ABC中,角A,B,C的对边分别为 ,且
,且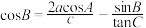 .若
.若 是
是 的“费马点”,
的“费马点”, .
.(1)求角
 ;
;(2)若
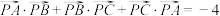 ,求
,求 的周长;
的周长;(3)在(2)的条件下,设
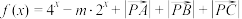 ,若当
,若当 时,不等式
时,不等式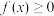 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-05-06更新
|
1038次组卷
|
10卷引用:宁夏回族自治区石嘴山市第三中学2023-2024学年高一下学期7月期末数学试题
宁夏回族自治区石嘴山市第三中学2023-2024学年高一下学期7月期末数学试题安徽省安庆市桐城中学2023-2024学年高一下学期4月月考数学试题(已下线)专题04 高一下期末考前必刷卷02(提高卷)-期末考点大串讲(人教A版2019必修第二册)(已下线)专题05 解三角形大题常考题型归类-期期末考点大串讲(人教B版2019必修第四册)青海省西宁市第十四中学2023-2024学年高一下学期6月月考数学试卷河南省信阳高级中学新校(贤岭校区)2023-2024学年高一下期6月检测(一)数学试题河北省石家庄市2023-2024学年高一下学期期末教学质量检测数学试卷河北省保定市唐县第一中学2023-2024学年高一下学期7月期末考试数学试题湖南省汨罗市第一中学2023-2024学年高一下学期7月期末数学试题安徽省皖北县中联盟(省重点高中)2023-2024学年高一下学期期中联考数学A卷
名校
解题方法
4 . 已知 的内角A、B、C对的边分别为a,b,c,
的内角A、B、C对的边分别为a,b,c,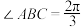 ,D为边AC上一点,满足
,D为边AC上一点,满足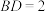 且
且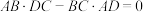 ,则
,则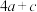 的最小值为
的最小值为_________ .
 的内角A、B、C对的边分别为a,b,c,
的内角A、B、C对的边分别为a,b,c,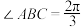 ,D为边AC上一点,满足
,D为边AC上一点,满足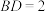 且
且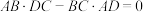 ,则
,则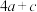 的最小值为
的最小值为
您最近一年使用:0次
名校
解题方法
5 . 已知向量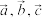 满足
满足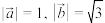 ,
,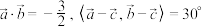 ,则
,则 的最大值等于( )
的最大值等于( )
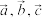 满足
满足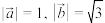 ,
,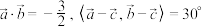 ,则
,则 的最大值等于( )
的最大值等于( )A. | B.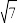 | C.2 | D. |
您最近一年使用:0次
2024-04-01更新
|
1624次组卷
|
12卷引用:宁夏回族自治区石嘴山市第一中学2023-2024学年高一下学期5月期中数学试题
宁夏回族自治区石嘴山市第一中学2023-2024学年高一下学期5月期中数学试题北京市第八十中学2023-2024学年高一下学期3月阶段测试数学试题(已下线)模块五 专题六 全真拔高模拟2(已下线)模块五 专题6 全真拔高模拟2(北师版高一期中)辽宁省东北育才学校科学高中部2023-2024学年高一下学期期中考试数学试题(已下线)专题05解三角形压轴小题归类(2) -期末考点大串讲(苏教版(2019))西安市交大附中2023—2024学年高一下学期第二次月考数学试题江苏省盐城市亭湖高级中学2023-2024学年高一下学期期中考试数学试题2019年广西柳州高中、南宁二中两校联考高三上学期第一次考试数学(理)试题河北省正定中学(实验中学)2019-2020学年高三下学期第三次阶段质量检测数学(理)试题湖南省衡阳市衡阳县第一中学2024届高三下学期4月月考数学试题(已下线)第7题 平面向量基本量的计算(2024高考真题) (一题多解)
名校
解题方法
6 . 在 中,角A,B,C的对边分别为a,b,c,且
中,角A,B,C的对边分别为a,b,c,且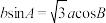 ,若点M是
,若点M是 的中点,且
的中点,且 ,则
,则
______ .
 中,角A,B,C的对边分别为a,b,c,且
中,角A,B,C的对边分别为a,b,c,且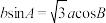 ,若点M是
,若点M是 的中点,且
的中点,且 ,则
,则
您最近一年使用:0次
2024-03-27更新
|
385次组卷
|
2卷引用:宁夏回族自治区石嘴山市第一中学2023-2024学年高一下学期5月期中数学试题
7 . 如图,在正三棱柱 中,
中, 为
为 的中点,点
的中点,点 在
在 上,
上, ,点
,点 在直线
在直线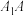 上,对于线段
上,对于线段 上异于两端点的任一点
上异于两端点的任一点 ,恒有
,恒有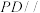 平面
平面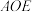 .
.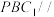 平面
平面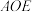 ;
;
(2)当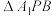 的面积取得最大值时,求二面角
的面积取得最大值时,求二面角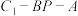 的余弦值.
的余弦值.
 中,
中, 为
为 的中点,点
的中点,点 在
在 上,
上, ,点
,点 在直线
在直线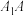 上,对于线段
上,对于线段 上异于两端点的任一点
上异于两端点的任一点 ,恒有
,恒有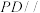 平面
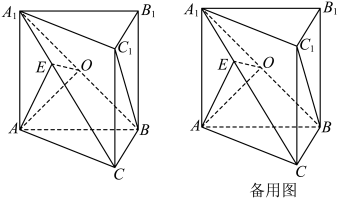
平面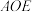 .
.
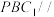 平面
平面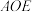 ;
;(2)当
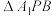 的面积取得最大值时,求二面角
的面积取得最大值时,求二面角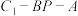 的余弦值.
的余弦值.
您最近一年使用:0次
2023-08-01更新
|
1542次组卷
|
7卷引用:宁夏吴忠市2022-2023学年高一下学期期末联合调研考试数学试题
宁夏吴忠市2022-2023学年高一下学期期末联合调研考试数学试题(已下线)第八章 立体几何初步(单元重点综合测试)-单元速记·巧练(人教A版2019必修第二册)(已下线)13.2.4 平面与平面的位置关系(2)-【帮课堂】(苏教版2019必修第二册)(已下线)专题02 高一下期末真题精选(2)-期末考点大串讲(人教A版2019必修第二册)(已下线)专题08立体几何期末14种常考题型归类(2) -期末真题分类汇编(人教B版2019必修第四册)(已下线)【一题多解】立体几何 新旧呼应(已下线)第二章 立体几何中的计算 专题一 空间角 微点10 二面角大小的计算综合训练【培优版】
8 . 某数学建模活动小组在开展主题为“空中不可到达两点的测距问题的探究活动中,抽象并构建了如图所示的几何模型,该模型中MA,NB均与水平面ABC垂直.在已测得可直接到达的两点间距离AC,BC的情况下,四名同学用测角仪各自测得下列四组角中的一组角的度数,其中一定能唯一确定M,N之间的距离的有( )
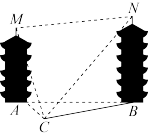
| A.∠MCA,∠NCB,∠ABC | B.∠ACB,∠NCB,∠MCN |
| C.∠MCA,∠NCB,∠MCN | D.∠MCA,∠NCB,∠ACB |
您最近一年使用:0次
2023-08-01更新
|
914次组卷
|
5卷引用:宁夏吴忠市2022-2023学年高一下学期期末联合调研考试数学试题
9 . 请从① ;②
;② ;③
;③ 这三个条件中任选一个,补充在下列问题中,并加以解答.(如未作出选择,则按照选择①评分)
这三个条件中任选一个,补充在下列问题中,并加以解答.(如未作出选择,则按照选择①评分)
在 中,a,b,c分别是角A,B,C的对边,若__________.
中,a,b,c分别是角A,B,C的对边,若__________.
(1)求角B的大小;
(2)若 为锐角三角形,
为锐角三角形, ,求
,求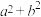 的取值范围.
的取值范围.
 ;②
;② ;③
;③ 这三个条件中任选一个,补充在下列问题中,并加以解答.(如未作出选择,则按照选择①评分)
这三个条件中任选一个,补充在下列问题中,并加以解答.(如未作出选择,则按照选择①评分)在
 中,a,b,c分别是角A,B,C的对边,若__________.
中,a,b,c分别是角A,B,C的对边,若__________.(1)求角B的大小;
(2)若
 为锐角三角形,
为锐角三角形, ,求
,求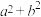 的取值范围.
的取值范围.
您最近一年使用:0次
2023-08-01更新
|
1146次组卷
|
5卷引用:宁夏银川市第二中学2022-2023学年高一下学期期末考试数学试题
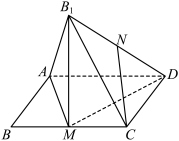
10 . 如图,在菱形ABCD中, ,
, ,M为BC的中点,将
,M为BC的中点,将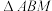 沿直线AM翻折成
沿直线AM翻折成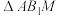 ,连接
,连接 和
和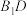 ,N为
,N为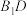 的中点,则( )
的中点,则( )
 ,
, ,M为BC的中点,将
,M为BC的中点,将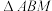 沿直线AM翻折成
沿直线AM翻折成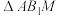 ,连接
,连接 和
和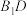 ,N为
,N为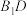 的中点,则( )
的中点,则( )
A.平面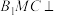 平面AMCD 平面AMCD |
| B.线段CN的长为定值 |
C.当三棱锥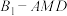 的体积最大时,三棱锥 的体积最大时,三棱锥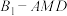 的外接球表面积为 的外接球表面积为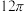 |
D.直线AM和CN所成的角始终为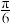 |
您最近一年使用:0次
2023-08-01更新
|
768次组卷
|
3卷引用:宁夏银川市第二中学2022-2023学年高一下学期期末考试数学试题



