名校
1 . 设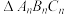 的三边长分别为
的三边长分别为 ,
, ,
,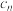 ,
, ,2,3,
,2,3, ,若
,若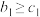 ,
,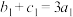 ,
, ,
, ,
,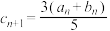 ,则当
,则当 最大时,
最大时,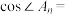
________ .
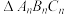 的三边长分别为
的三边长分别为 ,
, ,
,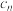 ,
, ,2,3,
,2,3, ,若
,若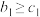 ,
,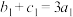 ,
, ,
, ,
,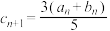 ,则当
,则当 最大时,
最大时,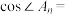
您最近一年使用:0次
2 . 已知 的前
的前 项和是
项和是 ,且
,且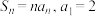 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设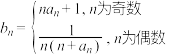 求数列
求数列 的前
的前 项和
项和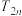 .
.
 的前
的前 项和是
项和是 ,且
,且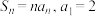 .
.(1)求数列
 的通项公式;
的通项公式;(2)设
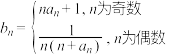 求数列
求数列 的前
的前 项和
项和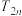 .
.
您最近一年使用:0次
2024-07-22更新
|
400次组卷
|
2卷引用:云南省保山市2023-2024学年高二下学期期末质量检测数学试题
3 . 已知数列 满足
满足 ,
,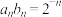 ,数列
,数列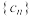 满足
满足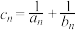 .
.
(1)判断数列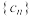 的单调性;
的单调性;
(2)求数列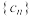 的前n项和
的前n项和 .
.
 满足
满足 ,
,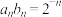 ,数列
,数列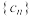 满足
满足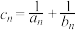 .
.(1)判断数列
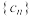 的单调性;
的单调性;(2)求数列
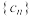 的前n项和
的前n项和 .
.
您最近一年使用:0次
2024-06-21更新
|
216次组卷
|
3卷引用:云南省普洱市2023-2024学年高二下学期7月期末统测数学试题
4 . 已知数列 满足
满足 ,
,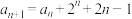 .
.
(1)求 ,
, ;
;
(2)求 ,并判断
,并判断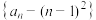 是否为等比数列.
是否为等比数列.
 满足
满足 ,
,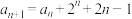 .
.(1)求
 ,
, ;
;(2)求
 ,并判断
,并判断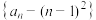 是否为等比数列.
是否为等比数列.
您最近一年使用:0次
2024-03-29更新
|
500次组卷
|
2卷引用:云南省楚雄彝族自治州2024届高三上学期期末数学试题
名校
解题方法
5 . 如图的形状出现在南宋数学家杨辉所著的《详解九章算法•商功》中,后人称为“三角垛”.“三角垛”最上层有1个球,第二层有3个球,第三层有6个球,……第 层有
层有 个球,则数列
个球,则数列 的前30项和为( )
的前30项和为( )
 层有
层有 个球,则数列
个球,则数列 的前30项和为( )
的前30项和为( )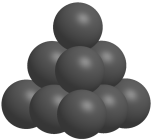
A.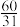 | B.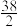 | C.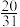 | D.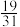 |
您最近一年使用:0次
2024-03-26更新
|
624次组卷
|
4卷引用:云南省曲靖市师宗县平高中学(第四中学)2023-2024学年高二下学期期末考试数学试题
解题方法
6 . 下列说法正确的是( )
A.若等比数列 的公比为 的公比为 ,则其前 ,则其前 项和为 项和为 |
B.已知数列 为等差数列,若 为等差数列,若 (其中 (其中 、 、 、 、 、 、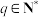 ),则 ),则 |
C.若数列 的通项公式为 的通项公式为 ,其前 ,其前 项和为 项和为 ,则 ,则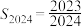 |
D.若数列 的首项为 的首项为 ,其前 ,其前 项和为 项和为 ,且 ,且 ,则 ,则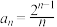 |
您最近一年使用:0次
7 . 任取一个正整数,若是奇数,就将该数乘3再加上1;若是偶数,就将该数除以2,反复进行上述两种计算,经过有限步后,必进入循环 .这就是数学史上著名的“冰雹猜想”.事实上“冰雹猜想”的递推关系如下:已知数列
.这就是数学史上著名的“冰雹猜想”.事实上“冰雹猜想”的递推关系如下:已知数列 满足:
满足: (
( 为正整数),
为正整数),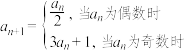 ,若
,若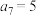 ,则
,则 的值可以是( )
的值可以是( )
 .这就是数学史上著名的“冰雹猜想”.事实上“冰雹猜想”的递推关系如下:已知数列
.这就是数学史上著名的“冰雹猜想”.事实上“冰雹猜想”的递推关系如下:已知数列 满足:
满足: (
( 为正整数),
为正整数),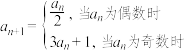 ,若
,若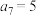 ,则
,则 的值可以是( )
的值可以是( )| A.12 | B.13 | C.40 | D.80 |
您最近一年使用:0次
解题方法
8 . 已知数列 满足
满足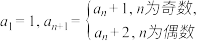 .
.
(1)求 ;
;
(2)求数列 的通项公式
的通项公式 .
.
 满足
满足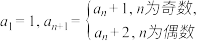 .
.(1)求
 ;
;(2)求数列
 的通项公式
的通项公式 .
.
您最近一年使用:0次
2024-01-13更新
|
825次组卷
|
5卷引用:云南省玉溪市2023-2024学年高二上学期期末教学质量检测数学试卷
云南省玉溪市2023-2024学年高二上学期期末教学质量检测数学试卷(已下线)专题01求数列通项公式9种常考题型归类【好题汇编】-备战2023-2024学年高二数学下学期期末真题分类汇编(北师大版2019选择性必修第二册)(已下线)5.2.1 等差数列(4知识点+8题型+强化训练)-【帮课堂】2023-2024学年高二数学同步学与练(人教B版2019选择性必修第三册)(已下线)1.2.1 等差数列的概念及其通项公式8种常见考法归类(3)(已下线)专题1 数列奇偶项、子数列求和压轴题【练】(高二期末压轴专项)
9 . 斐波那契数列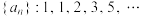 ,又称黄金分割数列或兔子数列.此数列从第3项开始,每一项都等于前两项之和,记
,又称黄金分割数列或兔子数列.此数列从第3项开始,每一项都等于前两项之和,记 为数列
为数列 的前
的前 项和,下列结论正确的是( )
项和,下列结论正确的是( )
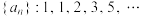 ,又称黄金分割数列或兔子数列.此数列从第3项开始,每一项都等于前两项之和,记
,又称黄金分割数列或兔子数列.此数列从第3项开始,每一项都等于前两项之和,记 为数列
为数列 的前
的前 项和,下列结论正确的是( )
项和,下列结论正确的是( )A.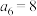 | B.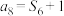 |
C.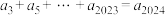 | D.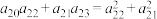 |
您最近一年使用:0次
解题方法
10 . 已知数列 满足
满足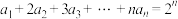 .
.
(1)求数列 的通项公式;
的通项公式;
(2)数列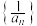 的前
的前 项和为
项和为 ,求证:
,求证: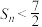 .
.
 满足
满足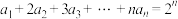 .
.(1)求数列
 的通项公式;
的通项公式;(2)数列
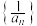 的前
的前 项和为
项和为 ,求证:
,求证: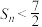 .
.
您最近一年使用:0次



