真题
解题方法
1 . 设函数 .
.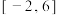 上画出函数
上画出函数 的图象;
的图象;
(2)设集合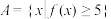 ,
,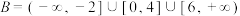 .试判断集合
.试判断集合 和
和 之间的关系,并给出证明;
之间的关系,并给出证明;
(3)当 时,求证:在区间
时,求证:在区间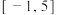 上,
上, 的图象位于函数
的图象位于函数 图象的上方.
图象的上方.
 .
.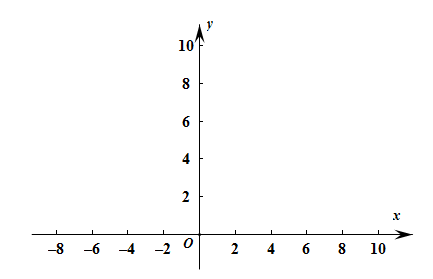
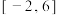 上画出函数
上画出函数 的图象;
的图象;(2)设集合
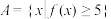 ,
,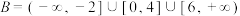 .试判断集合
.试判断集合 和
和 之间的关系,并给出证明;
之间的关系,并给出证明;(3)当
 时,求证:在区间
时,求证:在区间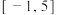 上,
上, 的图象位于函数
的图象位于函数 图象的上方.
图象的上方.
您最近一年使用:0次
2016-12-04更新
|
566次组卷
|
5卷引用:2017届江西南昌新课标高三一轮复习训练三数学试卷
2017届江西南昌新课标高三一轮复习训练三数学试卷2006年普通高等学校春季招生考试数学试题(上海卷)北京名校2023届高三一轮总复习 第2章 函数与导数 2.8 函数的图象(已下线)专题11 不等式中的恒成立问题的求解策略(一题多变)(已下线)专题02+二次函数-2020-2021学年新教材高一数学寒假辅导讲义(沪教版2020)
名校
解题方法
2 . 已知函数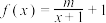 ,
,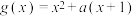 .
.
(1)当 ,
, 时,解关于
时,解关于 的不等式
的不等式 ;
;
(2)当 时,对任意
时,对任意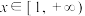 ,关于
,关于 的不等式
的不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当 ,
, 时,若点
时,若点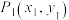 ,
,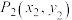 均为函数
均为函数 与函数
与函数 图象的公共点,且
图象的公共点,且 ,求证:
,求证: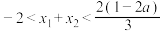 .
.
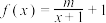 ,
,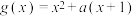 .
.(1)当
 ,
, 时,解关于
时,解关于 的不等式
的不等式 ;
;(2)当
 时,对任意
时,对任意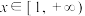 ,关于
,关于 的不等式
的不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)当
 ,
, 时,若点
时,若点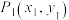 ,
,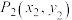 均为函数
均为函数 与函数
与函数 图象的公共点,且
图象的公共点,且 ,求证:
,求证: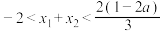 .
.
您最近一年使用:0次
2024-08-14更新
|
549次组卷
|
3卷引用:四川德阳市博雅明德高级中学2023-2024学年高三高考适应性考试数学试题
名校
解题方法
3 . 已知直线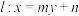 交抛物线
交抛物线 于
于 两点,
两点, 为
为 的焦点,且
的焦点,且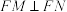 .
.
(1)证明: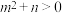 ;
;
(2)求 的取值范围.
的取值范围.
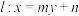 交抛物线
交抛物线 于
于 两点,
两点, 为
为 的焦点,且
的焦点,且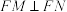 .
.(1)证明:
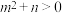 ;
;(2)求
 的取值范围.
的取值范围.
您最近一年使用:0次
2024-07-22更新
|
249次组卷
|
2卷引用:江西省抚州市多所学校2025届高三下学期第一次大联考数学试题
解题方法
4 . 数值线性代数又称矩阵计算,是计算数学的一个重要分支,其主要研究对象包括向量和矩阵.对于平面向量 ,其模定义为
,其模定义为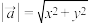 .类似地,对于
.类似地,对于 行
行 列的矩阵
列的矩阵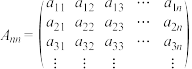 ,其模可由向量模拓展为
,其模可由向量模拓展为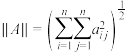 (其中
(其中 为矩阵中第
为矩阵中第 行第
行第 列的数,
列的数, 为求和符号),记作
为求和符号),记作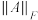 ,我们称这样的矩阵模为弗罗贝尼乌斯范数,例如对于矩阵
,我们称这样的矩阵模为弗罗贝尼乌斯范数,例如对于矩阵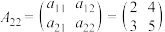 ,其矩阵模
,其矩阵模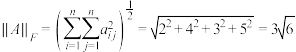 .弗罗贝尼乌斯范数在机器学习等前沿领域有重要的应用.
.弗罗贝尼乌斯范数在机器学习等前沿领域有重要的应用.
(1)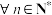 ,
, ,矩阵
,矩阵 ,求使
,求使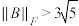 的
的 的最小值.
的最小值.
(2)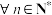 ,
, ,,矩阵
,,矩阵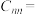
 求
求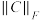 .
.
(3)矩阵 ,证明:
,证明: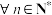 ,
, ,
,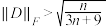 .
.
 ,其模定义为
,其模定义为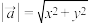 .类似地,对于
.类似地,对于 行
行 列的矩阵
列的矩阵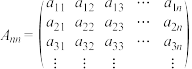 ,其模可由向量模拓展为
,其模可由向量模拓展为 (其中
(其中 为矩阵中第
为矩阵中第 行第
行第 列的数,
列的数, 为求和符号),记作
为求和符号),记作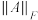 ,我们称这样的矩阵模为弗罗贝尼乌斯范数,例如对于矩阵
,我们称这样的矩阵模为弗罗贝尼乌斯范数,例如对于矩阵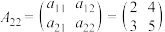 ,其矩阵模
,其矩阵模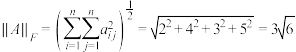 .弗罗贝尼乌斯范数在机器学习等前沿领域有重要的应用.
.弗罗贝尼乌斯范数在机器学习等前沿领域有重要的应用.(1)
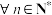 ,
, ,矩阵
,矩阵 ,求使
,求使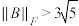 的
的 的最小值.
的最小值.(2)
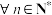 ,
, ,,矩阵
,,矩阵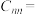
 求
求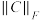 .
.(3)矩阵
 ,证明:
,证明: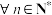 ,
, ,
,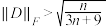 .
.
您最近一年使用:0次
名校
解题方法
5 . 已知函数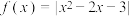 .
.
(1)求不等式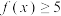 的解集;
的解集;
(2)设函数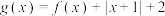 的最小值为
的最小值为 ,若
,若 且
且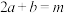 ,求证:
,求证: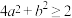 .
.
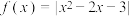 .
.(1)求不等式
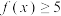 的解集;
的解集;(2)设函数
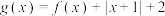 的最小值为
的最小值为 ,若
,若 且
且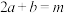 ,求证:
,求证: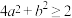 .
.
您最近一年使用:0次
2024-02-05更新
|
936次组卷
|
8卷引用:陕西省安康中学等校2023-2024学年高三上学期1月大联考文科数学试题(全国乙卷)
名校
解题方法
6 . 已知函数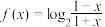 .
.
(1)判断并证明 的奇偶性;
的奇偶性;
(2)若对任意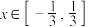 ,
, ,不等式
,不等式 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
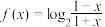 .
.(1)判断并证明
 的奇偶性;
的奇偶性;(2)若对任意
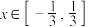 ,
, ,不等式
,不等式 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
您最近一年使用:0次
2024-09-12更新
|
2504次组卷
|
5卷引用:江苏省南通市2025届高三九月份调研考试数学试题
江苏省南通市2025届高三九月份调研考试数学试题安徽省六安第二中学2024-2025学年高三上学期第二次月考(10月)数学试题重庆市乌江新高考协作体2025届高三上学期高考质量调研(二)(10月)数学试题山东省聊城第一中学2025届高三上学期第一次月考数学试题(已下线)4.2.3 对数函数的性质与图象+4.3 指数函数与对数函数的关系——课后作业(提升版)
解题方法
7 . 已知函数 对任意实数
对任意实数 恒有
恒有 成立,且当
成立,且当 时,
时,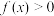 .
.
(1)求
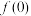 的值;
的值;(2)判断
 的单调性,并证明;
的单调性,并证明;(3)解关于
 的不等式:
的不等式: .
.
您最近一年使用:0次
名校
解题方法
8 . 已知函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 .
.
(1)求 ,
, 的值;
的值;
(2)用定义法证明函数 在
在 上单调递增;
上单调递增;
(3)若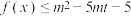 对于任意的
对于任意的 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 .
.(1)求
 ,
, 的值;
的值;(2)用定义法证明函数
 在
在 上单调递增;
上单调递增;(3)若
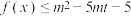 对于任意的
对于任意的 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-08-17更新
|
2698次组卷
|
20卷引用:黑龙江省鸡西实验中学2023-2024学年高三上学期第一次考试数学试题
黑龙江省鸡西实验中学2023-2024学年高三上学期第一次考试数学试题四川省南充市第一中学2022-2023学年高一上学期11月月考数学试题(已下线)高一上学期期中考试解答题压轴题50题专练-举一反三系列吉林省长春汽车经济技术开发区第三中学2023-2024学年高一上学期10月月考数学试题云南省下关第一中学2023-2024学年高一上学期10月月考数学试题湖北省荆州市沙市中学2023-2024学年高一上学期10月月考数学试题(已下线)专题02 高一上期中真题精选-期中考点大串讲(人教A版2019必修第一册)广东省中山市龙山中学2023-2024学年高一上学期10月月考数学试题广东省广州市第六十五中学2023-2024学年高一上学期期中数学试题四川省内江市第二中学2023-2024学年高一上学期期中考试数学试题(已下线)高一数学上学期期中考试模拟卷山东省淄博第七中学2023-2024学年高一上学期期中考试数学试题四川省成都市第二十中学校2023-2024学年高一上学期期中数学试题广东省江门市第一中学2023-2024学年高一上学期第二次段考数学试题(已下线)必修第一册综合检测(基础)-【优化数学】单元测试基础卷(人教A版2019)广东省江门市第一中学2023-2024学年高一下学期启超班期中数学试题(已下线)专题3 函数性质的综合应用【讲】(高一期中压轴专项)解答题新疆维吾尔自治区喀什地区巴楚县2024-2025学年高一上学期10月期中考试数学试题江苏省扬州市扬州大学附属中学东部分校2023-2024学年高一上学期期中考试数学试卷广州市白云区广州空港实验中学2024-2025学年高一上学期期中考试数学试题
名校
解题方法
9 . 已知函数 满足
满足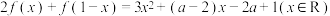 .
.
(1)讨论 的奇偶性;
的奇偶性;
(2)设函数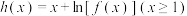 ,求证:
,求证: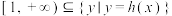 .
.
 满足
满足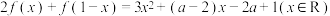 .
.(1)讨论
 的奇偶性;
的奇偶性;(2)设函数
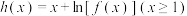 ,求证:
,求证: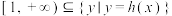 .
.
您最近一年使用:0次
10 . 已知函数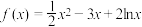 .
.
(1)求曲线 在点
在点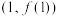 处的切线方程;
处的切线方程;
(2)(ⅰ)若对于任意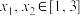 ,都有
,都有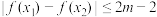 ,求实数
,求实数 的取值范围;
的取值范围;
(ⅱ)设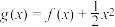 ,且
,且 ,求证:
,求证: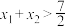 .
.
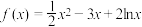 .
.(1)求曲线
 在点
在点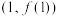 处的切线方程;
处的切线方程;(2)(ⅰ)若对于任意
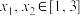 ,都有
,都有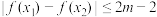 ,求实数
,求实数 的取值范围;
的取值范围;(ⅱ)设
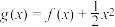 ,且
,且 ,求证:
,求证: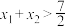 .
.
您最近一年使用:0次



