1 . 陀螺是中国民间最早的娱乐工具之一.图1是一种木陀螺,可近似地看作是一个圆锥和一个圆柱的组合体,其直观图如图2所示,其中 分别是上、下底面圆的圆心,且
分别是上、下底面圆的圆心,且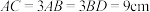 ,现有一箱这种的陀螺共重
,现有一箱这种的陀螺共重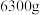 (不包含箱子的质量),陀螺的密度为
(不包含箱子的质量),陀螺的密度为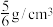 (
( 取3)
取3)
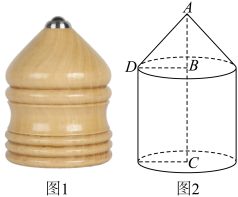
(1)试问该箱中有多少个这样的陀螺?
(2)如果要给这箱陀螺的每个表面涂上一种特殊的颜料,试问共需涂多少 的颜料?
的颜料?
 分别是上、下底面圆的圆心,且
分别是上、下底面圆的圆心,且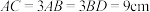 ,现有一箱这种的陀螺共重
,现有一箱这种的陀螺共重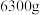 (不包含箱子的质量),陀螺的密度为
(不包含箱子的质量),陀螺的密度为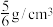 (
( 取3)
取3)
(1)试问该箱中有多少个这样的陀螺?
(2)如果要给这箱陀螺的每个表面涂上一种特殊的颜料,试问共需涂多少
 的颜料?
的颜料?
您最近一年使用:0次
2024-05-29更新
|
414次组卷
|
4卷引用:河北省衡水市故城县河北郑口中学2023-2024学年高一下学期7月期末数学试题
河北省衡水市故城县河北郑口中学2023-2024学年高一下学期7月期末数学试题广东实验中学2023-2024学年高一下学期第二次段考数学试题浙江省杭州地区(含周边)重点中学2023-2024学年高一下学期4月期中考试数学试题(已下线)专题07 空间几何体-【暑假自学课】(人教B版2019必修第四册)
解题方法
2 . 如图,已知三棱锥 的三条侧棱
的三条侧棱 ,
, ,
, 两两垂直,且
两两垂直,且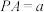 ,
,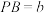 ,
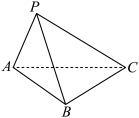
,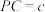 ,三棱锥
,三棱锥 的外接球半径
的外接球半径 .
. 的侧面积
的侧面积 的最大值;
的最大值;
(2)若在底面 上,有一个小球由顶点
上,有一个小球由顶点 处开始随机沿底边自由滚动,每次滚动一条底边,滚向顶点
处开始随机沿底边自由滚动,每次滚动一条底边,滚向顶点 的概率为
的概率为 ,滚向顶点
,滚向顶点 的概率为
的概率为 ;当球在顶点
;当球在顶点 处时,滚向顶点
处时,滚向顶点 的概率为
的概率为 ,滚向顶点
,滚向顶点 的概率为
的概率为 ;当球在顶点
;当球在顶点 处时,滚向顶点
处时,滚向顶点 的概率为
的概率为 ,滚向顶点
,滚向顶点 的概率为
的概率为 .若小球滚动3次,记球滚到顶点
.若小球滚动3次,记球滚到顶点 处的次数为
处的次数为 ,求数学期望
,求数学期望 的值.
的值.
 的三条侧棱
的三条侧棱 ,
, ,
, 两两垂直,且
两两垂直,且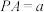 ,
,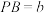 ,
,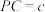 ,三棱锥
,三棱锥 的外接球半径
的外接球半径 .
.
 的侧面积
的侧面积 的最大值;
的最大值;(2)若在底面
 上,有一个小球由顶点
上,有一个小球由顶点 处开始随机沿底边自由滚动,每次滚动一条底边,滚向顶点
处开始随机沿底边自由滚动,每次滚动一条底边,滚向顶点 的概率为
的概率为 ,滚向顶点
,滚向顶点 的概率为
的概率为 ;当球在顶点
;当球在顶点 处时,滚向顶点
处时,滚向顶点 的概率为
的概率为 ,滚向顶点
,滚向顶点 的概率为
的概率为 ;当球在顶点
;当球在顶点 处时,滚向顶点
处时,滚向顶点 的概率为
的概率为 ,滚向顶点
,滚向顶点 的概率为
的概率为 .若小球滚动3次,记球滚到顶点
.若小球滚动3次,记球滚到顶点 处的次数为
处的次数为 ,求数学期望
,求数学期望 的值.
的值.
您最近一年使用:0次
解题方法
3 . 已知四棱锥 的体积为1,底面
的体积为1,底面 为平行四边形,
为平行四边形, ,
, 分别是
分别是 ,
, 上的点,
上的点, ,
,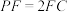 ,平面
,平面 交
交 于点
于点 .
.
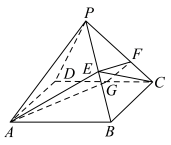
(1)求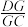 ;
;
(2)求多面体 的体积.
的体积.
 的体积为1,底面
的体积为1,底面 为平行四边形,
为平行四边形, ,
, 分别是
分别是 ,
, 上的点,
上的点, ,
,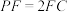 ,平面
,平面 交
交 于点
于点 .
.
(1)求
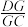 ;
;(2)求多面体
 的体积.
的体积.
您最近一年使用:0次
解题方法
4 . 在正三棱锥 中,
中,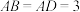 ,点
,点 在线段
在线段 上.过点
上.过点 作平行于
作平行于 和
和 的平面
的平面 ,分别交棱
,分别交棱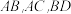 于点M,N,O.
于点M,N,O.

(1)证明:四边形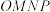 为矩形;
为矩形;
(2)若 ,求多面体MNPOBC的体积.
,求多面体MNPOBC的体积.
 中,
中,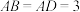 ,点
,点 在线段
在线段 上.过点
上.过点 作平行于
作平行于 和
和 的平面
的平面 ,分别交棱
,分别交棱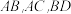 于点M,N,O.
于点M,N,O.
(1)证明:四边形
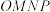 为矩形;
为矩形;(2)若
 ,求多面体MNPOBC的体积.
,求多面体MNPOBC的体积.
您最近一年使用:0次
名校
5 . 如图,长方体 中,AB=AD=2,A
中,AB=AD=2,A =4,P为棱
=4,P为棱 的中点.
的中点.
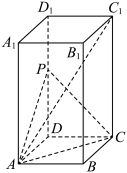
(1)求直线 与平面
与平面 所成角的余弦值;
所成角的余弦值;
(2)求直线AP被长方体 的外接球截得的线段长度.
的外接球截得的线段长度.
 中,AB=AD=2,A
中,AB=AD=2,A =4,P为棱
=4,P为棱 的中点.
的中点.
(1)求直线
 与平面
与平面 所成角的余弦值;
所成角的余弦值;(2)求直线AP被长方体
 的外接球截得的线段长度.
的外接球截得的线段长度.
您最近一年使用:0次
名校
6 . 如图,四棱锥 中,四边形
中,四边形 为矩形,
为矩形, ,
,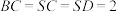 ,
, .
.
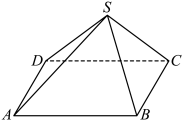
(1)求证: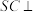 平面
平面 ;
;
(2)求四棱锥 外接球的体积.
外接球的体积.
 中,四边形
中,四边形 为矩形,
为矩形, ,
,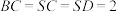 ,
, .
.
(1)求证:
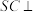 平面
平面 ;
;(2)求四棱锥
 外接球的体积.
外接球的体积.
您最近一年使用:0次
2020-07-23更新
|
392次组卷
|
2卷引用:河北省保定市2019-2020学年高一下学期期末数学试题
名校
解题方法
7 . 已知四棱台 中,
中,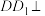 平面ABCD,四边形ABCD为平行四边形,
平面ABCD,四边形ABCD为平行四边形,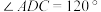 ,
,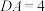 ,
,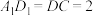 ,
,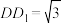 ,E为DC中点.
,E为DC中点.

(1)求证: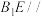 平面
平面 ;
;
(2)求证: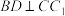 ;
;
(3)求三棱锥 的高.
的高.
(注:棱台的两底面相似)
 中,
中,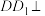 平面ABCD,四边形ABCD为平行四边形,
平面ABCD,四边形ABCD为平行四边形,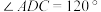 ,
,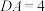 ,
,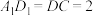 ,
,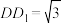 ,E为DC中点.
,E为DC中点.
(1)求证:
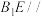 平面
平面 ;
;(2)求证:
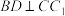 ;
;(3)求三棱锥
 的高.
的高.(注:棱台的两底面相似)
您最近一年使用:0次
名校
8 . 如图所示,如果一个几何体的正视图与侧视图是全等的长方形,且边长分别是4与2,俯视图是一个边长为4的正方形

(Ⅰ)求该几何体的表面积;
(Ⅱ)求该几何体的外接球的体积

(Ⅰ)求该几何体的表面积;
(Ⅱ)求该几何体的外接球的体积
您最近一年使用:0次
2018-08-03更新
|
441次组卷
|
2卷引用:【全国市级联考】河北省张家口市2017-2018学年高一下学期期末考试数学试题



