1 . 如图,在四棱锥 中,
中, 底面ABCD,
底面ABCD,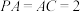 ,
, ,
,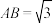 .
. ,求:向量
,求:向量 在向量
在向量 上的投影向量的模;
上的投影向量的模;
(2)当 ,且
,且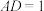 时,四棱锥
时,四棱锥 是否有外接球?若有,请求出四棱锥
是否有外接球?若有,请求出四棱锥 的外接球的表面积.
的外接球的表面积.
(3)若 ,且
,且 ,求二面角
,求二面角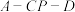 的正切值.
的正切值.
 中,
中, 底面ABCD,
底面ABCD,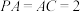 ,
, ,
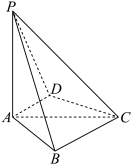
,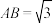 .
.
 ,求:向量
,求:向量 在向量
在向量 上的投影向量的模;
上的投影向量的模;(2)当
 ,且
,且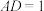 时,四棱锥
时,四棱锥 是否有外接球?若有,请求出四棱锥
是否有外接球?若有,请求出四棱锥 的外接球的表面积.
的外接球的表面积.(3)若
 ,且
,且 ,求二面角
,求二面角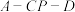 的正切值.
的正切值.
您最近一年使用:0次
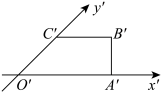
2 . 如图所示,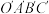 为四边形OABC的斜二测直观图,其中
为四边形OABC的斜二测直观图,其中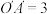 ,
,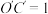 ,
, .
. 的平面图并标出边长,并求平面四边形
的平面图并标出边长,并求平面四边形 的面积;
的面积;
(2)若该四边形 以OA为旋转轴,旋转一周,求旋转形成的几何体的体积及表面积.
以OA为旋转轴,旋转一周,求旋转形成的几何体的体积及表面积.
 为四边形OABC的斜二测直观图,其中
为四边形OABC的斜二测直观图,其中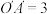 ,
,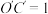 ,
, .
.
 的平面图并标出边长,并求平面四边形
的平面图并标出边长,并求平面四边形 的面积;
的面积;(2)若该四边形
 以OA为旋转轴,旋转一周,求旋转形成的几何体的体积及表面积.
以OA为旋转轴,旋转一周,求旋转形成的几何体的体积及表面积.
您最近一年使用:0次
2024-03-20更新
|
881次组卷
|
11卷引用:安徽省太和中学2023-2024学年高一下学期6月期末考试数学试题
安徽省太和中学2023-2024学年高一下学期6月期末考试数学试题福建省宁德市同心顺联盟2021-2022学年高一下学期期中联合考试数学试题(已下线)8.2直观图(已下线)8.2 立体图形的直观图(2)-2022-2023学年高一数学《考点·题型·技巧》精讲与精练高分突破系列(人教A版2019必修第二册)(已下线)专题8.4 立体图形的直观图(重难点题型检测)-2022-2023学年高一数学举一反三系列(人教A版2019必修第二册)(已下线)高一数学下学期期中模拟试卷(第6章-第8章8.3)-【题型分类归纳】2022-2023学年高一数学同步讲与练(人教A版2019必修第二册)江西省寻乌中学2022-2023学年高一下学期第二次阶段性测试(6月)数学试题(已下线)专题09 立体几何(5大易错点分析+解题模板+举一反三+易错题通关)-1(已下线)专题8.13 立体几何初步全章综合测试卷(提高篇)-举一反三系列福建省三明市尤溪县第七中学2023-2024学年高一下学期期中考试数学试题河北省保定市六校联盟2023-2024学年高一下学期期中联考数学试题
解题方法
3 . 如图,在正四棱柱 中,
中,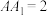 ,
, ∥平面MAC.
∥平面MAC.
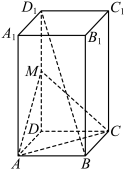
(1)证明:M是 的中点;
的中点;
(2)若正四棱柱的外接球的体积是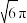 ,求该正四棱柱的表面积.
,求该正四棱柱的表面积.
 中,
中,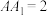 ,
, ∥平面MAC.
∥平面MAC.
(1)证明:M是
 的中点;
的中点;(2)若正四棱柱的外接球的体积是
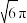 ,求该正四棱柱的表面积.
,求该正四棱柱的表面积.
您最近一年使用:0次
2023-07-28更新
|
630次组卷
|
2卷引用:安徽省宣城市2022-2023学年高一下学期期末调研测试数学试卷
名校
解题方法
4 . 如图,在多面体 中,平面
中,平面 平面
平面 ,四边形
,四边形 为菱形,
为菱形,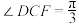 ,底面
,底面 为直角梯形,
为直角梯形, ,
, ,
,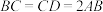 .
.
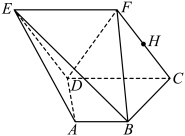
(1)证明: ;
;
(2)若 ,求多面体
,求多面体 的体积.
的体积.
 中,平面
中,平面 平面
平面 ,四边形
,四边形 为菱形,
为菱形,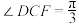 ,底面
,底面 为直角梯形,
为直角梯形, ,
, ,
,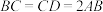 .
.
(1)证明:
 ;
;(2)若
 ,求多面体
,求多面体 的体积.
的体积.
您最近一年使用:0次
名校
解题方法
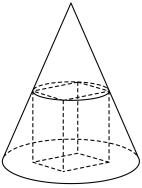
5 . 如图所示是在圆锥内部挖去一正四棱柱所形成的几何体,该正四棱柱上底面的四顶点在圆锥侧面上,下底面落在圆锥底面内,已知圆锥侧面积为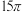 ,底面半径为
,底面半径为 .
. ,求该几何体的体积;
,求该几何体的体积;
(Ⅱ)求该几何体内正四棱柱侧面积的最大值.
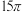 ,底面半径为
,底面半径为 .
.
 ,求该几何体的体积;
,求该几何体的体积;(Ⅱ)求该几何体内正四棱柱侧面积的最大值.
您最近一年使用:0次
2021-08-13更新
|
1281次组卷
|
8卷引用:安徽省合肥一六八中学2023-2024学年高一下学期期末素养测试数学试卷
安徽省合肥一六八中学2023-2024学年高一下学期期末素养测试数学试卷福建省宁德市高中同心顺联盟校2020-2021学年高一下学期期中考试数学试题(已下线)8.3 简单几何体的表面积与体积(精练)-2021-2022学年高一数学一隅三反系列(人教A版2019必修第二册)广东省广州市八校联考2021-2022学年高一下学期期中数学(B卷)试题湖南省邵阳市武冈市2021-2022学年高一下学期期中数学试题(已下线)8.3简单几何体的表面积和体积(第2课时)(练案)-2021-2022学年高一数学同步备课 (人教A版2019 必修第二册)云南省昆明市第一中学2021-2022学年高一下学期期中考试数学试题四川省广安市第二中学校2022-2023学年高一下学期期中考试数学试题
解题方法
6 . 如图,四边形 是边长为4的菱形,
是边长为4的菱形, ,
, 平面
平面 ,将菱形
,将菱形 沿对角线
沿对角线 折起,使得点
折起,使得点 到达点
到达点 的位置,且平面
的位置,且平面 平面
平面 .
.
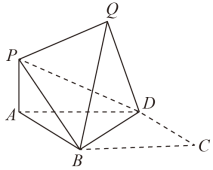
(1)求证: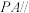 平面
平面 ;
;
(2)若点 在同一个球面上,求三棱锥
在同一个球面上,求三棱锥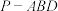 与三棱锥
与三棱锥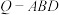 的公共部分的体积.
的公共部分的体积.
 是边长为4的菱形,
是边长为4的菱形,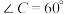 ,
, 平面
平面 ,将菱形
,将菱形 沿对角线
沿对角线 折起,使得点
折起,使得点 到达点
到达点 的位置,且平面
的位置,且平面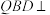 平面
平面 .
.
(1)求证:
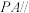 平面
平面 ;
;(2)若点
 在同一个球面上,求三棱锥
在同一个球面上,求三棱锥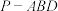 与三棱锥
与三棱锥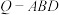 的公共部分的体积.
的公共部分的体积.
您最近一年使用:0次
7 . 某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面相同,圆柱有上底面,制作时接头忽略不计.已知圆柱的底面周长为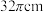 ,高为
,高为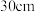 ,圆锥的母线长为
,圆锥的母线长为 .
.
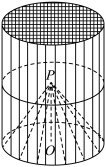
(1)求这种“笼具”的体积;
(2)现要使用一种纱网材料制作100个“笼具”,该材料的造价为每平方米4元,共需多少元?
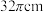 ,高为
,高为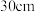 ,圆锥的母线长为
,圆锥的母线长为 .
.
(1)求这种“笼具”的体积;
(2)现要使用一种纱网材料制作100个“笼具”,该材料的造价为每平方米4元,共需多少元?
您最近一年使用:0次
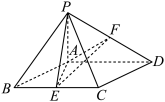
8 . 如图所示,四棱锥 中,
中, 菱形
菱形 所在的平面,
所在的平面, ,点
,点 、
、 分别是
分别是 、
、 的中点.
的中点.
(1)求证:平面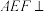 平面
平面 ;
;
(2)当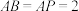 时,求多面体
时,求多面体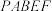 的体积.
的体积.
 中,
中, 菱形
菱形 所在的平面,
所在的平面, ,点
,点 、
、 分别是
分别是 、
、 的中点.
的中点.
(1)求证:平面
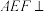 平面
平面 ;
;(2)当
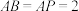 时,求多面体
时,求多面体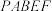 的体积.
的体积.
您最近一年使用:0次
2021-07-03更新
|
562次组卷
|
4卷引用:安徽省亳州市涡阳县第九中学2021-2022学年高一下学期期末数学试题
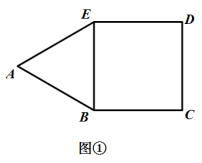
9 . 如图①,是由正三角形 和正方形
和正方形 组成的平面图形,其中
组成的平面图形,其中 ;将其沿
;将其沿 折起,使得
折起,使得 ,如图②所示.
,如图②所示.

(1)证明:图②中平面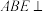 平面
平面 ;
;
(2)在线段 上取一点
上取一点 ,使
,使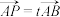 ,当三棱锥
,当三棱锥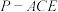 的体积为
的体积为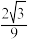 时,求
时,求 的值.
的值.
 和正方形
和正方形 组成的平面图形,其中
组成的平面图形,其中 ;将其沿
;将其沿 折起,使得
折起,使得 ,如图②所示.
,如图②所示.

(1)证明:图②中平面
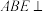 平面
平面 ;
;(2)在线段
 上取一点
上取一点 ,使
,使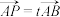 ,当三棱锥
,当三棱锥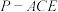 的体积为
的体积为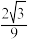 时,求
时,求 的值.
的值.
您最近一年使用:0次
2021-01-29更新
|
1931次组卷
|
7卷引用:安徽省宣城市2020-2021学年高三上学期期末数学(文)试题
安徽省宣城市2020-2021学年高三上学期期末数学(文)试题(已下线) 专题18 几何体的表面积与体积的求解 (测)-2021年高三数学二轮复习讲练测(新高考版)(已下线) 专题22 几何体的表面积与体积的求解 (测)-2021年高三数学二轮复习讲练测(文理通用)江西省赣州市南康区唐江中学2021届高三3月综合性考试数学(文)试题苏教版(2019) 必修第二册 过关斩将 章节测试 第13章 立体几何初步(已下线)专题5 综合闯关(提升版)(已下线)第31讲 空间几何体体积及点到面的距离问题4种题型
名校
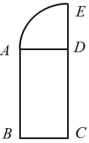
10 . 图形 由矩形
由矩形 和扇形
和扇形 组合而成(如图所示),
组合而成(如图所示),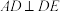 ,
, .求将该图形沿
.求将该图形沿 旋转一周后所形成的几何体的表面积和体积.
旋转一周后所形成的几何体的表面积和体积.
 由矩形
由矩形 和扇形
和扇形 组合而成(如图所示),
组合而成(如图所示),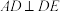 ,
, .求将该图形沿
.求将该图形沿 旋转一周后所形成的几何体的表面积和体积.
旋转一周后所形成的几何体的表面积和体积.
您最近一年使用:0次
2020-08-14更新
|
929次组卷
|
8卷引用:安徽省合肥世界外国语学校高中部2021-2022学年高一下学期期末数学试题
安徽省合肥世界外国语学校高中部2021-2022学年高一下学期期末数学试题四川省成都市2019-2020学年高一下学期期末(文科)数学试题四川省成都市2019~2020学年度下学期期末高一年级调研考试文科数学试题四川省成都市2019~2020学年度下学期期末高一年级调研考试理科数学试题四川省成都彭州市2019-2020学年高一下学期期末调研考试数学(文)试题安徽省合肥市第十中学2021-2022学年高一下学期期中数学试题(已下线)第一章+空间几何体(基础过关)-2020-2021学年高一数学单元测试定心卷(人教版必修2)新疆生产建设兵团第二师八一中学2023-2024学年高二上学期期中考试数学(理科)试题



