1 . 上海中心大厦是上海市的地标建筑,现为中国第一高楼.为有效减少建筑所受的风荷载,通常对建筑体型进行一定的扭转.上海中心大厦的主楼可近似看成将正三棱柱的一个底面扭转所得的几何体;将正三棱柱 的底面
的底面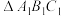 在其所在平面内绕
在其所在平面内绕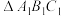 的中心逆时针旋转
的中心逆时针旋转 得到
得到 ,再分别连接
,再分别连接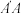 、
、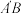 、
、 、
、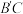 、
、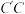 、
、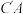 所得的几何体.已知大厦的主楼高度约为
所得的几何体.已知大厦的主楼高度约为 米,底层面积(即
米,底层面积(即 的面积)约为
的面积)约为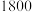 平方米.
平方米.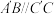 ;
;
(2)试分别以正三棱柱 和几何体
和几何体 为模型估算大厦主楼的体积.
为模型估算大厦主楼的体积.
 的底面
的底面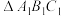 在其所在平面内绕
在其所在平面内绕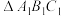 的中心逆时针旋转
的中心逆时针旋转 得到
得到 ,再分别连接
,再分别连接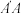 、
、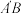 、
、 、
、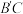 、
、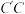 、
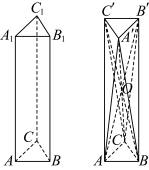
、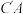 所得的几何体.已知大厦的主楼高度约为
所得的几何体.已知大厦的主楼高度约为 米,底层面积(即
米,底层面积(即 的面积)约为
的面积)约为 平方米.
平方米.
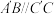 ;
;(2)试分别以正三棱柱
 和几何体
和几何体 为模型估算大厦主楼的体积.
为模型估算大厦主楼的体积.
您最近一年使用:0次
解题方法
2 . 对于一个三维空间,如果一个平面与一个球只有一个交点,则称这个平面是这个球的切平面.已知在空间直角坐标系 中,球
中,球 的半径为
的半径为 ,记平面
,记平面 、平面
、平面 、平面
、平面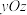 分别为
分别为 、
、 、
、 .
.
(1)若棱长为 的正方体、棱长为
的正方体、棱长为 的正四面体的内切球均为球
的正四面体的内切球均为球 ,求
,求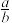 的值;
的值;
(2)若球 在
在 处有一切平面为
处有一切平面为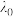 ,求
,求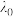 与
与 的交线方程,并写出它的一个法向量;
的交线方程,并写出它的一个法向量;
(3)如果在球面上任意一点作切平面 ,记
,记 与
与 、
、 、
、 的交线分别为
的交线分别为 、
、 、
、 ,求
,求 到
到 、
、 、
、 距离乘积的最小值.
距离乘积的最小值.
 中,球
中,球 的半径为
的半径为 ,记平面
,记平面 、平面
、平面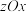 、平面
、平面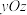 分别为
分别为 、
、 、
、 .
.(1)若棱长为
 的正方体、棱长为
的正方体、棱长为 的正四面体的内切球均为球
的正四面体的内切球均为球 ,求
,求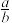 的值;
的值;(2)若球
 在
在 处有一切平面为
处有一切平面为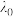 ,求
,求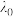 与
与 的交线方程,并写出它的一个法向量;
的交线方程,并写出它的一个法向量;(3)如果在球面上任意一点作切平面
 ,记
,记 与
与 、
、 、
、 的交线分别为
的交线分别为 、
、 、
、 ,求
,求 到
到 、
、 、
、 距离乘积的最小值.
距离乘积的最小值.
您最近一年使用:0次
2024-01-14更新
|
883次组卷
|
6卷引用:上海市普陀区桃浦中学2024届高三上学期期末数学试题
上海市普陀区桃浦中学2024届高三上学期期末数学试题(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大核心考点)(讲义)(已下线)第二章 立体几何中的计算 专题六 几何体的外接球、棱切球、内切球 微点15 几何体的内切球与棱切球(一)【基础版】(已下线)第七章 应用空间向量解立体几何问题拓展 专题二 平面法向量求法及其应用 微点2 平面法向量求法及其应用(二)【培优版】(已下线)专题4 立体几何中的新定义压轴大题(二)【讲】(已下线)专题5 解析几何中的新定义压轴大题(二)【讲】
3 . 我国古代数学名著《九章算术》,将底面为矩形且有一条侧棱垂直于底面的四棱锥称为“阳马”.如图所示,在长方体 中,已知
中,已知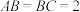 ,
, .
.
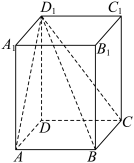
(1)求证:四棱锥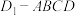 是一个“阳马”,并求该“阳马”的体积;
是一个“阳马”,并求该“阳马”的体积;
(2)求该“阳马”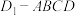 的外接球的表面积.
的外接球的表面积.
 中,已知
中,已知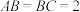 ,
, .
.
(1)求证:四棱锥
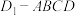 是一个“阳马”,并求该“阳马”的体积;
是一个“阳马”,并求该“阳马”的体积;(2)求该“阳马”
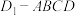 的外接球的表面积.
的外接球的表面积.
您最近一年使用:0次
4 . 某广场内设置了一些石凳供大家休息,这些石凳是由正方体截去八个一样的四面体得到的,如图所示,若被截正方体的棱长是60cm.
(2)为了美观工人准备将石凳的表面进行粉刷,已知每平方米造价50元,请问粉刷一个石凳需要多少钱?(精确到0.1元)

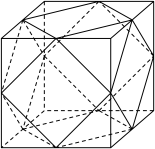
(2)为了美观工人准备将石凳的表面进行粉刷,已知每平方米造价50元,请问粉刷一个石凳需要多少钱?(精确到0.1元)
您最近一年使用:0次
2023-10-22更新
|
718次组卷
|
9卷引用:上海市青浦区朱家角中学2023-2024学年高二上学期期末考试数学试题
上海市青浦区朱家角中学2023-2024学年高二上学期期末考试数学试题上海市七宝中学2023-2024学年高二上学期10月月考数学试题上海市七宝中学2023-2024学年高二上学期9月月考数学试题(已下线)专题09 多面体与旋转体- 【暑假自学课】(沪教版2020)黑龙江省实验中学2022-2023学年高一下学期期中数学试题内蒙古自治区乌兰察布市衡水卓远中学2022-2023学年高一下学期6月月考数学试题辽宁省沈阳市翔宇中学2022-2023学年高一下学期第二次月考测试数学试题(已下线)模块三 专题5 大题分类练(空间几何体表面积和体积)(人教A版)(已下线)专题03 简单几何体的表面积和体积-《知识解读·题型专练》(人教A版2019必修第二册)
5 . 如果一个正多面体的所有面都是全等的正三角形或正多边形,每个顶点聚集的棱的条数都相等,这个多面体叫做正多面体.有趣的是只有正四面体、正方体、正八面体、正十二面体和正二十面体五种正多面体,现将它们的体积依次记为, .
.

(1)利用金属板分别制作正多面体模型各一个,假设制作每个模型的外壳用料(即表面积)均等于 ,分别求出
,分别求出 和
和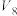 的值;并猜想
的值;并猜想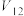 与
与 的大小关系(猜想不需证明)
的大小关系(猜想不需证明)
(2)多面体的欧拉定理:简单多面体的面数 、棱数
、棱数 与顶点数
与顶点数 满足:
满足: .已知正多面体都是简单多面体,设某个正多面体每个顶点聚集的棱的条数为
.已知正多面体都是简单多面体,设某个正多面体每个顶点聚集的棱的条数为 ,每个面的边数为
,每个面的边数为 ,求
,求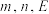 满足的关系式;并尝试据此说明正多面体仅有五种.
满足的关系式;并尝试据此说明正多面体仅有五种.
 .
.
(1)利用金属板分别制作正多面体模型各一个,假设制作每个模型的外壳用料(即表面积)均等于
 ,分别求出
,分别求出 和
和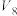 的值;并猜想
的值;并猜想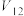 与
与 的大小关系(猜想不需证明)
的大小关系(猜想不需证明)(2)多面体的欧拉定理:简单多面体的面数
 、棱数
、棱数 与顶点数
与顶点数 满足:
满足: .已知正多面体都是简单多面体,设某个正多面体每个顶点聚集的棱的条数为
.已知正多面体都是简单多面体,设某个正多面体每个顶点聚集的棱的条数为 ,每个面的边数为
,每个面的边数为 ,求
,求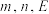 满足的关系式;并尝试据此说明正多面体仅有五种.
满足的关系式;并尝试据此说明正多面体仅有五种.
您最近一年使用:0次
名校
6 . 佩香囊是端午节传统习俗之一,香囊内通常填充一些中草药,有清香、驱虫等功效.因地方习俗的差异,香囊常用丝布做成各种不同的形状,形形色色,玲珑夺目,如图1所示的平行四边形ABCD由六个正三角形构成,将它沿虚线折起来,可得到图2所示的六面体形状的香囊.若 .
.
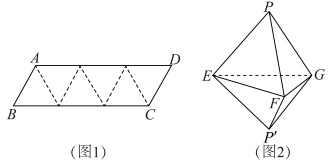
(1)求图2中六面体的表面积;
(2)求二面角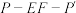 的大小.
的大小.
 .
.
(1)求图2中六面体的表面积;
(2)求二面角
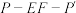 的大小.
的大小.
您最近一年使用:0次
名校
解题方法
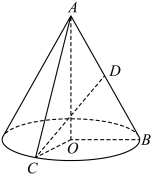
7 . 如图,在直角 中,
中,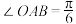 ,斜边
,斜边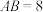 ,
, 是
是 中点,现将直角
中点,现将直角 以直角边
以直角边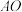 为轴旋转一周得到一个圆锥.点
为轴旋转一周得到一个圆锥.点 为圆锥底面圆周上一点,且
为圆锥底面圆周上一点,且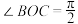 .
.
(2)求直线 与平面
与平面 所成的角的正切值.
所成的角的正切值.
 中,
中,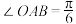 ,斜边
,斜边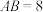 ,
, 是
是 中点,现将直角
中点,现将直角 以直角边
以直角边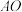 为轴旋转一周得到一个圆锥.点
为轴旋转一周得到一个圆锥.点 为圆锥底面圆周上一点,且
为圆锥底面圆周上一点,且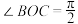 .
.
(2)求直线
 与平面
与平面 所成的角的正切值.
所成的角的正切值.
您最近一年使用:0次
2023-01-11更新
|
626次组卷
|
6卷引用:上海市浦东新区2022-2023学年高二上学期期末数学试题
上海市浦东新区2022-2023学年高二上学期期末数学试题(已下线)8.6.2直线与平面垂直的判定定理(第1课时)(精讲)(2)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)(已下线)13.2.3 直线和平面的位置关系(1)(已下线)专题10 空间角与空间距离的综合(1)-期中期末考点大串讲(已下线)上海市四校(复兴高级中学、松江二中、奉贤中学、金山中学)2024届高三下学期3月联考数学试题变式题17-21四川省内江市第一中学2023-2024学年高二上学期10月月考数学试题
名校
解题方法
8 . 已知正三棱锥 ,顶点为
,顶点为 ,底面是三角形
,底面是三角形 .
.

(1)若该三棱锥的侧棱长为1,且两两成角为 ,设质点
,设质点 自
自 出发依次沿着三个侧面移动环绕一周直至回到出发点
出发依次沿着三个侧面移动环绕一周直至回到出发点 ,求质点移动路程的最小值;
,求质点移动路程的最小值;
(2)若该三棱锥的所有棱长均为1,试求以 为顶点,以三角形
为顶点,以三角形 内切圆为底面的圆锥的体积;
内切圆为底面的圆锥的体积;
(3)若该三棱锥的底面边长为1,四个顶点在同一个球面上, 、
、 分别是
分别是 ,
, 的中点,且
的中点,且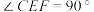 ,求此球的体积.
,求此球的体积.
 ,顶点为
,顶点为 ,底面是三角形
,底面是三角形 .
.
(1)若该三棱锥的侧棱长为1,且两两成角为
 ,设质点
,设质点 自
自 出发依次沿着三个侧面移动环绕一周直至回到出发点
出发依次沿着三个侧面移动环绕一周直至回到出发点 ,求质点移动路程的最小值;
,求质点移动路程的最小值;(2)若该三棱锥的所有棱长均为1,试求以
 为顶点,以三角形
为顶点,以三角形 内切圆为底面的圆锥的体积;
内切圆为底面的圆锥的体积;(3)若该三棱锥的底面边长为1,四个顶点在同一个球面上,
 、
、 分别是
分别是 ,
, 的中点,且
的中点,且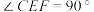 ,求此球的体积.
,求此球的体积.
您最近一年使用:0次
解题方法
9 . 由曲线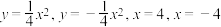 围成的封闭图形绕
围成的封闭图形绕 轴旋转一周所得的旋转体的体积为
轴旋转一周所得的旋转体的体积为 ;满足
;满足 的点
的点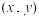 所组成的封闭图形绕
所组成的封闭图形绕 轴旋转一周所得的旋转体的体积为
轴旋转一周所得的旋转体的体积为
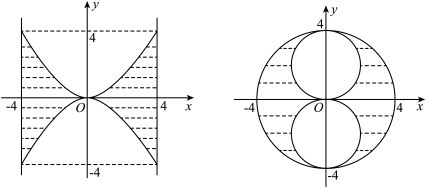
(1)当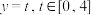 时,分别求出两旋转体的水平截面的面积
时,分别求出两旋转体的水平截面的面积 ;
;
(2)求 与
与 的关系,并说明理由.
的关系,并说明理由.
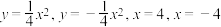 围成的封闭图形绕
围成的封闭图形绕 轴旋转一周所得的旋转体的体积为
轴旋转一周所得的旋转体的体积为 ;满足
;满足 的点
的点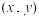 所组成的封闭图形绕
所组成的封闭图形绕 轴旋转一周所得的旋转体的体积为
轴旋转一周所得的旋转体的体积为

(1)当
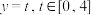 时,分别求出两旋转体的水平截面的面积
时,分别求出两旋转体的水平截面的面积 ;
;(2)求
 与
与 的关系,并说明理由.
的关系,并说明理由.
您最近一年使用:0次
10 . 如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成.已知球的直径为8cm,圆柱筒高为3cm.

(1)求这种“浮球”的体积;
(2)要在这样的3000个“浮球”的表面涂一层胶质,如果每平方厘米需要涂胶0.1克,共需胶多少克?

(1)求这种“浮球”的体积;
(2)要在这样的3000个“浮球”的表面涂一层胶质,如果每平方厘米需要涂胶0.1克,共需胶多少克?
您最近一年使用:0次
2023-01-05更新
|
942次组卷
|
10卷引用:上海市上海财经大学附属中学2022-2023学年高二上学期期末数学试题
上海市上海财经大学附属中学2022-2023学年高二上学期期末数学试题(已下线)8.3 简单几何体的表面积与体积(精练)-2022-2023学年高一数学一隅三反系列(人教A版2019必修第二册)(已下线)8.3.2圆柱、圆锥、圆台、球的表面积和体积(精练)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)河北省武强中学2022-2023学年高一下学期期中数学试题山东省青岛市青岛二中分校2022-2023学年高一下学期期中考试数学试题(已下线)6.6.3球的表面积和体积(课件+练习)(已下线)8.3.2 圆柱、圆锥、圆台、球的表面积和体积(1)-2022-2023学年高一数学《考点·题型·技巧》精讲与精练高分突破系列(人教A版2019必修第二册)(已下线)专题8.6 简单几何体的表面积与体积(重难点题型检测)-2022-2023学年高一数学举一反三系列(人教A版2019必修第二册)云南省曲靖市会泽县实验高级中学校2022-2023学年高一下学期月考数学试题(四)云南省红河州蒙自市红河哈尼族彝族自治州第一中学2022-2023学年高一下学期4月月考数学试题



