名校
1 . 如图1,在平行四边形 中,
中,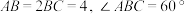 ,E为
,E为 的中点.将
的中点.将 沿
沿 折起,连接
折起,连接 与
与 ,如图2.
,如图2. 为何值时,平面
为何值时,平面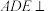 平面
平面 ?
?
(2)设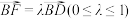 ,当
,当 时,是否存在实数
时,是否存在实数 ,使得直线
,使得直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)当三棱锥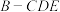 的体积最大时,求三棱锥
的体积最大时,求三棱锥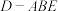 的内切球的半径.
的内切球的半径.
 中,
中,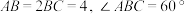 ,E为
,E为 的中点.将
的中点.将 沿
沿 折起,连接
折起,连接 与
与 ,如图2.
,如图2.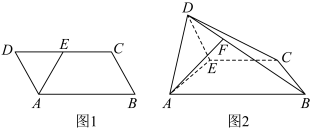
 为何值时,平面
为何值时,平面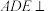 平面
平面 ?
?(2)设
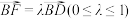 ,当
,当 时,是否存在实数
时,是否存在实数 ,使得直线
,使得直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(3)当三棱锥
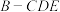 的体积最大时,求三棱锥
的体积最大时,求三棱锥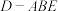 的内切球的半径.
的内切球的半径.
您最近一年使用:0次
2024-08-05更新
|
1335次组卷
|
4卷引用:广东省广州市越秀区2023-2024学年高一下学期期末数学试题
名校
2 . 如下左图,矩形 中,
中, ,
, ,
, .过顶点
.过顶点 作对角线
作对角线 的垂线,交对角线
的垂线,交对角线 于点
于点 ,交边
,交边 于点
于点 ,现将
,现将 沿
沿 翻折,形成四面体
翻折,形成四面体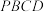 ,如下右图.
,如下右图.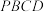 外接球的体积;
外接球的体积;
(2)求证:平面 平面
平面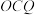 ;
;
(3)若点 为棱
为棱 的中点,请判断在将
的中点,请判断在将 沿
沿 翻折过程中,直线
翻折过程中,直线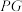 能否平行于面
能否平行于面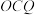 .若能请求出此时的二面角
.若能请求出此时的二面角 的大小;若不能,请说明理由.
的大小;若不能,请说明理由.
 中,
中, ,
, ,
, .过顶点
.过顶点 作对角线
作对角线 的垂线,交对角线
的垂线,交对角线 于点
于点 ,交边
,交边 于点
于点 ,现将
,现将 沿
沿 翻折,形成四面体
翻折,形成四面体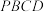 ,如下右图.
,如下右图.
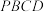 外接球的体积;
外接球的体积;(2)求证:平面
 平面
平面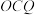 ;
;(3)若点
 为棱
为棱 的中点,请判断在将
的中点,请判断在将 沿
沿 翻折过程中,直线
翻折过程中,直线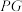 能否平行于面
能否平行于面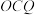 .若能请求出此时的二面角
.若能请求出此时的二面角 的大小;若不能,请说明理由.
的大小;若不能,请说明理由.
您最近一年使用:0次
2024-05-26更新
|
601次组卷
|
4卷引用:广东省湛江市2023-2024学年高一下学期期末调研测试数学试卷
广东省湛江市2023-2024学年高一下学期期末调研测试数学试卷安徽省级示范高中培优联盟2023-2024学年高一下学期春季联赛数学试题安徽省亳州市第二完全中学2023-2024学年高一下学期第二次月考(5月)数学试题(已下线)11.4.2 平面与平面垂直-【帮课堂】(人教B版2019必修第四册)
解题方法
3 . 如图I为某同学搭建的立体几何模型,相关性质如图描述,其侧面展开图如图II所示.图I中,圆锥 的半径为3,体积为12π. 在等腰
的半径为3,体积为12π. 在等腰 (可近似看作与扇形KUN重合)中,
(可近似看作与扇形KUN重合)中,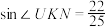 .中间圆柱展开图可看作正方形.圆柱J-G中,半径为3,体积为45π.侧面非阴影部分的圆边共占20%.设圆O所在平面为
.中间圆柱展开图可看作正方形.圆柱J-G中,半径为3,体积为45π.侧面非阴影部分的圆边共占20%.设圆O所在平面为 ,圆G所在平面为
,圆G所在平面为 ,各立方体平稳放置,回答以下问题:
,各立方体平稳放置,回答以下问题: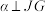 .
.
(2)试求K到G的距离及阴影部分面积.
 的半径为3,体积为12π. 在等腰
的半径为3,体积为12π. 在等腰 (可近似看作与扇形KUN重合)中,
(可近似看作与扇形KUN重合)中,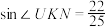 .中间圆柱展开图可看作正方形.圆柱J-G中,半径为3,体积为45π.侧面非阴影部分的圆边共占20%.设圆O所在平面为
.中间圆柱展开图可看作正方形.圆柱J-G中,半径为3,体积为45π.侧面非阴影部分的圆边共占20%.设圆O所在平面为 ,圆G所在平面为
,圆G所在平面为 ,各立方体平稳放置,回答以下问题:
,各立方体平稳放置,回答以下问题: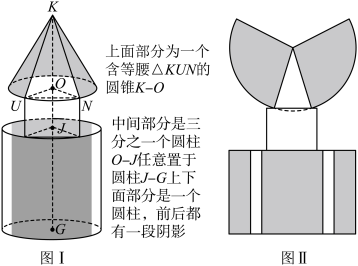
 .
.(2)试求K到G的距离及阴影部分面积.
您最近一年使用:0次
4 . 如图,在三棱柱 中,底面
中,底面 是边长为2的等边三角形,平面
是边长为2的等边三角形,平面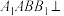 平面
平面 ,
,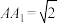 ,
, .
.
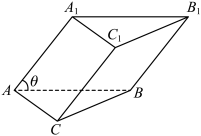
(1)当 时,求异面直线
时,求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(2)若存在球与三棱柱 各个面都相切,求
各个面都相切,求 的正弦值.
的正弦值.
 中,底面
中,底面 是边长为2的等边三角形,平面
是边长为2的等边三角形,平面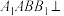 平面
平面 ,
,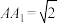 ,
, .
.
(1)当
 时,求异面直线
时,求异面直线 与
与 所成角的余弦值;
所成角的余弦值;(2)若存在球与三棱柱
 各个面都相切,求
各个面都相切,求 的正弦值.
的正弦值.
您最近一年使用:0次
名校
解题方法
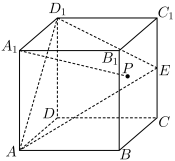
5 . 如图,在棱长为4的正方体 中,
中, 为
为 的中点,经过
的中点,经过 ,
, ,
, 三点的平面记为平面
三点的平面记为平面 ,点
,点 是侧面
是侧面 内的动点,且
内的动点,且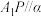 .
.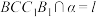 ,求证:
,求证: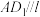 ;
;
(2)平面 将正方体
将正方体 分成两部分,求这两部分的体积之比
分成两部分,求这两部分的体积之比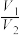 (其中
(其中 );
);
(3)当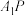 最小时,求三棱锥
最小时,求三棱锥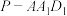 的外接球的表面积.
的外接球的表面积.
 中,
中, 为
为 的中点,经过
的中点,经过 ,
, ,
, 三点的平面记为平面
三点的平面记为平面 ,点
,点 是侧面
是侧面 内的动点,且
内的动点,且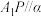 .
.
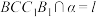 ,求证:
,求证: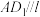 ;
;(2)平面
 将正方体
将正方体 分成两部分,求这两部分的体积之比
分成两部分,求这两部分的体积之比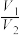 (其中
(其中 );
);(3)当
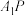 最小时,求三棱锥
最小时,求三棱锥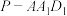 的外接球的表面积.
的外接球的表面积.
您最近一年使用:0次
2023-07-08更新
|
1584次组卷
|
5卷引用:广东省广州市越秀区2022-2023学年高一下学期期末数学试题
广东省广州市越秀区2022-2023学年高一下学期期末数学试题(已下线)第11章 简单几何体(压轴题专练)-2023-2024学年高二数学单元速记·巧练(沪教版2020必修第三册)(已下线)11.3.3平面与平面平行-同步精品课堂(人教B版2019必修第四册)(已下线)高一下学期期末复习解答题压轴题二十四大题型专练(2)-举一反三系列(人教A版2019必修第二册)安徽省安庆市怀宁县新安中学2023-2024学年高一下学期6月月考数学试卷
6 . 《九章算术》是中国古代的一部数学专著,是《算经十书》中最重要的一部,是当时世界上最简练有效的应用数学,它的出现标志着中国古代数学形成了完整的体系.《九章算术》中将由四个直角三角形组成的四面体称为“鳖臑”,已知四面体 是“鳖臑”,
是“鳖臑”,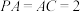 ,
, ,
, ,
, 分别为
分别为 ,
, 的中点,
的中点, 在线段
在线段 上,且
上,且 .
.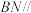 平面
平面 ;
;
(2)求四面体 内切球的表面积.
内切球的表面积.
 是“鳖臑”,
是“鳖臑”,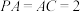 ,
, ,
, ,
, 分别为
分别为 ,
, 的中点,
的中点, 在线段
在线段 上,且
上,且 .
.
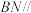 平面
平面 ;
;(2)求四面体
 内切球的表面积.
内切球的表面积.
您最近一年使用:0次
2023-06-27更新
|
855次组卷
|
6卷引用:广东省珠海东方外语实验学校2022-2023学年高一下学期期末数学试题
广东省珠海东方外语实验学校2022-2023学年高一下学期期末数学试题江苏省盐城市2022-2023学年高一下学期期末数学试题(已下线)压轴题立体几何新定义题(九省联考第19题模式)讲(已下线)第二章 立体几何中的计算 专题三 空间面积的计算 微点1 空间面积的计算【基础版】(已下线)高一下学期期中复习解答题压轴题十八大题型专练(2)-举一反三系列(人教A版2019必修第二册)【江苏专用】专题11立体几何与空间向量(第二部分)-高一下学期名校期末好题汇编
名校
解题方法
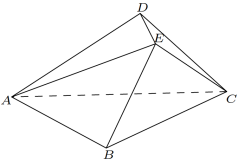
7 . 如图,在几何体 中,底面
中,底面 为以
为以 为斜边的等腰直角三角形.已知平面
为斜边的等腰直角三角形.已知平面 平面
平面 ,平面
,平面 平面
平面
 平面
平面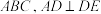 .
. 平面
平面 ;
;
(2)若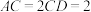 ,设
,设 为棱
为棱 的中点,求当几何体
的中点,求当几何体 的体积取最大值时
的体积取最大值时 与
与 所成角的正切值.
所成角的正切值.
 中,底面
中,底面 为以
为以 为斜边的等腰直角三角形.已知平面
为斜边的等腰直角三角形.已知平面 平面
平面 ,平面
,平面 平面
平面
 平面
平面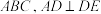 .
.
 平面
平面 ;
;(2)若
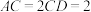 ,设
,设 为棱
为棱 的中点,求当几何体
的中点,求当几何体 的体积取最大值时
的体积取最大值时 与
与 所成角的正切值.
所成角的正切值.
您最近一年使用:0次
2022-10-03更新
|
3537次组卷
|
10卷引用:广东省深圳市高级中学2023-2024学年高三上学期第三次诊断测试数学试题
广东省深圳市高级中学2023-2024学年高三上学期第三次诊断测试数学试题湖北省二十一所重点中学2023届高三上学期第三次联考数学试题(已下线)考向30 立体几何中的最值、翻折、探索性问题(重点)(已下线)第07讲 向量法求距离、探索性及折叠问题 (高频考点—精讲)湖南省长沙市长郡中学2023届高三上学期第三次月考数学试题湖南省怀化市湖天中学2022-2023学年高三上学期11月月考数学试题(已下线)专题6 第3讲 立体几何中的向量方法2024届高三新高考改革数学适应性练习(九省联考题型)(已下线)专题15 立体几何解答题全归类(练习)(已下线)高考一轮单元复习验收卷·数学(十一)空间向量与立体几何
名校
8 . 如图,在正三棱锥 中,有一半径为1的半球,其底面圆O与正三棱锥的底面贴合,正三棱锥的三个侧面都和半球相切.设点D为BC的中点,
中,有一半径为1的半球,其底面圆O与正三棱锥的底面贴合,正三棱锥的三个侧面都和半球相切.设点D为BC的中点, .
. 分别表示线段BC和PD长度;
分别表示线段BC和PD长度;
(2)当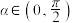 时,求三棱锥的侧面积S的最小值.
时,求三棱锥的侧面积S的最小值.
 中,有一半径为1的半球,其底面圆O与正三棱锥的底面贴合,正三棱锥的三个侧面都和半球相切.设点D为BC的中点,
中,有一半径为1的半球,其底面圆O与正三棱锥的底面贴合,正三棱锥的三个侧面都和半球相切.设点D为BC的中点, .
.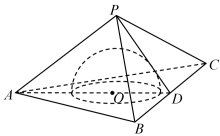
 分别表示线段BC和PD长度;
分别表示线段BC和PD长度;(2)当
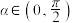 时,求三棱锥的侧面积S的最小值.
时,求三棱锥的侧面积S的最小值.
您最近一年使用:0次
2022-01-18更新
|
1970次组卷
|
6卷引用:广东省中山市2021-2022学年高二下学期期末数学试题
广东省中山市2021-2022学年高二下学期期末数学试题山东省烟台市2021-2022学年高三上学期期末数学试题江西省吉安市第一中学2024届高三“九省联考”考后适应性测试数学试题(一)(已下线)新题型01 新高考新结构二十一大考点汇总-3(已下线)专题04 立体几何山东省烟台第一中学2023届高三上学期1月考试数学试题
20-21高一下·广东广州·期末
名校
解题方法
9 . 如图,多面体 中,
中, 是菱形,
是菱形, ,
,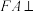 平面
平面 ,
, ,且
,且 .
.
(1)求证: 平面
平面 ;
;
(2)求多面体 的体积.
的体积.
 中,
中, 是菱形,
是菱形, ,
, 平面
平面 ,
, ,且
,且 .
.
(1)求证:
 平面
平面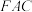 ;
;(2)求多面体
 的体积.
的体积.
您最近一年使用:0次
10 . 如图,梯形 中,
中, ,
, ,且
,且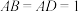 ,
,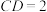 .现选择梯形的某一边为轴旋转一周,请说明所得到的几何体的构成并计算该几何体的体积.
.现选择梯形的某一边为轴旋转一周,请说明所得到的几何体的构成并计算该几何体的体积.
注:若有多种选择分别解答,按第一种选择的解答给分.
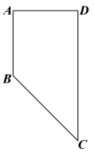
 中,
中, ,
, ,且
,且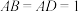 ,
,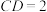 .现选择梯形的某一边为轴旋转一周,请说明所得到的几何体的构成并计算该几何体的体积.
.现选择梯形的某一边为轴旋转一周,请说明所得到的几何体的构成并计算该几何体的体积.注:若有多种选择分别解答,按第一种选择的解答给分.

您最近一年使用:0次



