解题方法
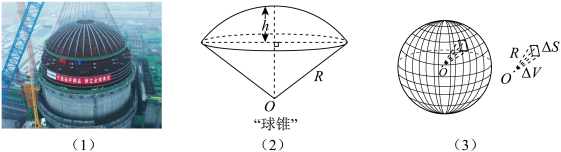
1 . 据报道,2024年4月15日,正值全民国家安全教育日,田湾核电8号机组穹顶球冠吊装成功(如图(1)),标志着国内最重核电机组薄壳钢衬里穹顶吊装工作安全完成,有力推动了我国产业结构和能源结构的调整,助力“双碳”目标顺利实现.报道中提到的球冠是一个空间几何概念,它是指球面被一个平面所截得的一部分(不包含截面),垂直于截面的直径被截得的部分是球冠的高.球冠面积等于截得它的球面上大圆(过球心的截面圆)周长与球冠的高的乘积.和球冠相对应的几何体叫球缺,它是指球体被一个平面所截得的一部分,截面是球缺的底.当球缺的高小于球半径时,我们把球缺与以球缺的底为底、以球心为顶点的圆锥所构成的体,称作“球锥”(如图(2))当一个四面体各顶点都在“球锥”表面上时,称这个四面体内接此“球锥”.如图(2),设一个“球锥”所在球的半径为 ,其中球冠高为
,其中球冠高为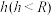 .
.
(2)在该“球锥”中,当球缺的体积与圆锥的体积相等时,求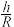 的值;
的值;
(3)已知一个棱长为 的正四面体内接此“球锥”,并且有一个顶点与球心重合,若满足条件的
的正四面体内接此“球锥”,并且有一个顶点与球心重合,若满足条件的 有且只有一个,求
有且只有一个,求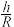 的取值范围.
的取值范围.
 ,其中球冠高为
,其中球冠高为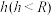 .
.
(2)在该“球锥”中,当球缺的体积与圆锥的体积相等时,求
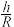 的值;
的值;(3)已知一个棱长为
 的正四面体内接此“球锥”,并且有一个顶点与球心重合,若满足条件的
的正四面体内接此“球锥”,并且有一个顶点与球心重合,若满足条件的 有且只有一个,求
有且只有一个,求 的取值范围.
的取值范围.
您最近一年使用:0次
2024-06-27更新
|
373次组卷
|
3卷引用:河南省部分学校2023-2024学年高一下学期联合教学质量检测数学试卷
23-24高一下·四川成都·阶段练习
名校
解题方法
2 . 在四面体 中,
中, ,记四面体
,记四面体 的内切球半径为
的内切球半径为 .分别过点
.分别过点 向其对面作垂线,垂足分别为
向其对面作垂线,垂足分别为 .
.
(1)是否存在四个面都是直角三角形的四面体 ?(不用说明理由)
?(不用说明理由)
(2)若垂足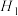 恰为正三角形
恰为正三角形 的中心,证明:
的中心,证明: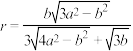 ;
;
(3)已知 ,证明:
,证明: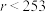 .
.
 中,
中,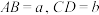 ,记四面体
,记四面体 的内切球半径为
的内切球半径为 .分别过点
.分别过点 向其对面作垂线,垂足分别为
向其对面作垂线,垂足分别为 .
.(1)是否存在四个面都是直角三角形的四面体
 ?(不用说明理由)
?(不用说明理由)(2)若垂足
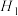 恰为正三角形
恰为正三角形 的中心,证明:
的中心,证明: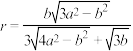 ;
;(3)已知
 ,证明:
,证明: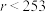 .
.
您最近一年使用:0次
2024-06-14更新
|
438次组卷
|
3卷引用:河南省三门峡市卢氏县第一高级中学2023-2024学年高一下期期末考试数学试题
河南省三门峡市卢氏县第一高级中学2023-2024学年高一下期期末考试数学试题四川省成都市石室中学2023-2024学年高一竞赛班下学期期末考试数学试题(已下线)四川省成都市第七中学2023-2024学高一下学期6月月考数学试题
22-23高一下·河南南阳·期末
解题方法
3 . 如图是一个以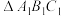 为底面的正三棱柱被一平面所截得的几何体,截面为
为底面的正三棱柱被一平面所截得的几何体,截面为 .已知
.已知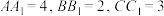 .
.

(1)在边 上是否存在一点
上是否存在一点 ,使得
,使得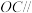 平面
平面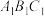 ?若存在,求出
?若存在,求出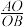 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(2)若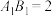 ,求几何体
,求几何体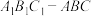 的体积.
的体积.
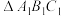 为底面的正三棱柱被一平面所截得的几何体,截面为
为底面的正三棱柱被一平面所截得的几何体,截面为 .已知
.已知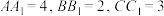 .
.
(1)在边
 上是否存在一点
上是否存在一点 ,使得
,使得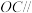 平面
平面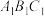 ?若存在,求出
?若存在,求出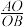 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;(2)若
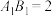 ,求几何体
,求几何体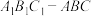 的体积.
的体积.
您最近一年使用:0次
名校
解题方法
4 . 如图,在直三棱柱 中,
中, ,侧面
,侧面 为正方形,点D,E,F,G分别为棱
为正方形,点D,E,F,G分别为棱 ,
, ,
, ,
, 的中点.
的中点.
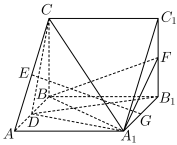
(1)求证:GE 平面
平面 ;
;
(2)若二面角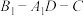 的余弦值为
的余弦值为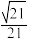 ,且
,且 ,求多面体
,求多面体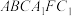 的体积.
的体积.
 中,
中, ,侧面
,侧面 为正方形,点D,E,F,G分别为棱
为正方形,点D,E,F,G分别为棱 ,
, ,
, ,
, 的中点.
的中点.
(1)求证:GE
 平面
平面 ;
;(2)若二面角
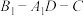 的余弦值为
的余弦值为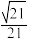 ,且
,且 ,求多面体
,求多面体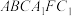 的体积.
的体积.
您最近一年使用:0次
名校
解题方法
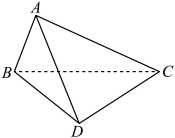
5 . 如图,四面体ABCD中,O,E分别是BD,BC的中点,CA=CB=CD=BD=2,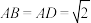 .
.
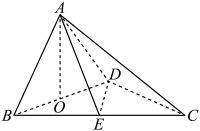
(1)求证: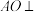 平面BCD;
平面BCD;
(2)求点E到平面ACD的距离.
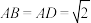 .
.
(1)求证:
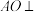 平面BCD;
平面BCD;(2)求点E到平面ACD的距离.
您最近一年使用:0次
2022-12-17更新
|
984次组卷
|
7卷引用:河南省郑州市励德双语学校2022-2023学年高三上学期期末考试文科数学试题
河南省郑州市励德双语学校2022-2023学年高三上学期期末考试文科数学试题吉林省四平市第一高级中学2021-2022学年高三上学期期末考试数学(文)试题山西省大同市博盛中学2022-2023学年高二下学期期末数学试题(已下线)8.6.2直线与平面垂直的判定定理(第1课时)(精练)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)(已下线)8.6.2直线与平面垂直的判定定理(第1课时)(精讲)(1)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)(已下线)微专题17 空间中的五种距离问题(1)(已下线)8.6.2 直线与平面垂直(1) -2022-2023学年高一数学《考点·题型·技巧》精讲与精练高分突破系列(人教A版2019必修第二册)
名校
解题方法
6 . 我市论语广场准备设置一些多面体形或球形的石凳供市民休息,如图(1)的多面体石凳是由图(2)的正方体石块截去八个相同的四面体得到,且该石凳的体积是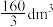 .
.
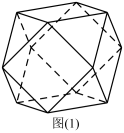
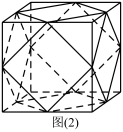
(Ⅰ)求正方体石块的棱长;
(Ⅱ)若将图(2)的正方体石块打磨成一个球形的石凳,求此球形石凳的最大体积.
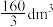 .
.

(Ⅰ)求正方体石块的棱长;
(Ⅱ)若将图(2)的正方体石块打磨成一个球形的石凳,求此球形石凳的最大体积.
您最近一年使用:0次
2021-02-02更新
|
862次组卷
|
3卷引用:河南省濮阳市2020-2021学年高一上学期期末数学试题
河南省濮阳市2020-2021学年高一上学期期末数学试题(已下线)专题8.2 简单几何体的表面积与体积(B卷提升篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教A版,浙江专用)广东省揭阳市揭西县河婆中学2020-2021学年高一下学期期中数学试题
7 . 已知,在三棱锥 中,
中,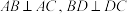 ,且
,且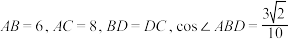
(1)求证:平面 平面
平面
(2)若 是三棱锥
是三棱锥 外接球上任一点,求三棱锥
外接球上任一点,求三棱锥 体积的最大值.
体积的最大值.
 中,
中,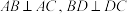 ,且
,且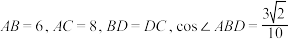

(1)求证:平面
 平面
平面
(2)若
 是三棱锥
是三棱锥 外接球上任一点,求三棱锥
外接球上任一点,求三棱锥 体积的最大值.
体积的最大值.
您最近一年使用:0次
11-12高二上·广东·期中
名校
解题方法
8 . 一个几何体由圆锥和圆柱组成,其尺寸如图所示.
(2)如果点 在直观图中所示位置,
在直观图中所示位置, 为所在母线中点,
为所在母线中点, 为母线与底面圆的交点,求在几何体表面上,从
为母线与底面圆的交点,求在几何体表面上,从 点到
点到 点的最短路径长.
点的最短路径长.
(2)如果点
 在直观图中所示位置,
在直观图中所示位置, 为所在母线中点,
为所在母线中点, 为母线与底面圆的交点,求在几何体表面上,从
为母线与底面圆的交点,求在几何体表面上,从 点到
点到 点的最短路径长.
点的最短路径长.
您最近一年使用:0次
2021-05-17更新
|
1653次组卷
|
34卷引用:河南省郑州市二中2015-2016学年高一上学期期末数学试题
河南省郑州市二中2015-2016学年高一上学期期末数学试题(已下线)2013-2014学年福建省晋江市季延中学高一下学期期末考试数学试卷【市级联考】吉林省公主岭市2018-2019学年高二上学期期末考试数学(文)试题四川省成都市温江区2019-2020学年度高一下学期期末考试数学试题吉林省长春市实验中学2019-2020学年高一下学期期末考试数学(文科)试卷吉林省长春市实验中学2019-2020学年高一下学期期末考试数学(理)试卷河南省信阳市光山县第二高级中学2023-2024学年高一下学期4月期中考试数学试题(已下线)2011-2012学年度广东省东山中学高二第一学期期中理科数学试卷2015-2016学年福建省龙海市程溪中学高一下期中数学试卷2016-2017学年山西怀仁县一中高二理上学期期中数学试卷2016-2017学年山西怀仁县一中高二文上学期期中数学试卷北京市东城区171中学2016-2017高二上学期期中考试数学(文)试题【全国百强校】河北省邢台市第一中学2017-2018学年高一下学期第三次月考数学(文)试题【全国百强校】四川省成都市外国语学校2018-2019学年高一5月月考数学试题四川省乐山市十校2019-2020学年高二上学期期中数学(文)试题四川省乐山十校2019-2020学年高二上学期期中联考数学(理)试题甘肃省天水市甘谷一中2019-2020学年高一上学期第二次月考数学试题云南省昆明市东川区明月中学2018-2019学年高一下学期期中考试数学试题(已下线)专题8.1 空间几何体的结构及其表面积、体积-2021年高考数学(理)一轮复习-题型全归纳与高效训练突破(已下线)专题8.1 空间几何体的结构及其表面积、体积-2021年高考数学(文)一轮复习-题型全归纳与高效训练突破(已下线)专题8.2 空间几何体的表面积和体积(精练)-2021年高考数学(理)一轮复习讲练测(已下线)专题8.2 空间几何体的表面积和体积 (精练)-2021年高考数学(理)一轮复习学与练山东省泰安肥城市2020-2021学年高一下学期期中考试数学试题上海市复旦大学附属中学2021-2022学年高二上学期期中数学试题山西省运城市景胜中学2021-2022学年高二下学期4月月考数学(文)试题山西省运城市景胜中学2021-2022学年高二下学期4月月考数学(理)试题(已下线)期中模拟预测卷02(测试范围:空间向量与立体几何)-2022-2023学年高二数学上学期期中期末考点大串讲(沪教版2020必修第三册+选修一)(已下线)第09讲 空间几何体的结构与直观图(核心考点讲与练)(2)四川省乐山市草堂高级中学2022-2023学年高二上学期期中数学试题(已下线)8.1基本立体图形(第2课时圆柱、圆锥、圆台、球的结构特征简单组合体的结构特征)(精讲)(1)精讲)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)湖北省武汉市第一中学2022-2023学年高一下学期5月月考数学试题(已下线)高一数学下学期期中精选50题(基础版)-2021-2022学年高一数学考试满分全攻略(人教A版2019必修第二册)(原卷版)上海市民办新虹桥中学2023-2024学年高二上学期期中考试数学试卷(已下线)11.1.5 旋转体-【帮课堂】(人教B版2019必修第四册)
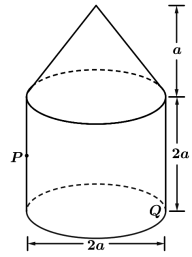
9 . 如图,在长方体ABCD-A1B1C1D1中,AB=BC= ,AA1=
,AA1= .
.
(1)求证:直线A1B∥平面ACD1
(2)已知三棱锥D1一BCD的所有顶点在同一个球面上,求这个球的体积
 ,AA1=
,AA1= .
.
(1)求证:直线A1B∥平面ACD1
(2)已知三棱锥D1一BCD的所有顶点在同一个球面上,求这个球的体积
您最近一年使用:0次
10 . 《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形的直棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵 与刍童
与刍童 的组合体中
的组合体中 ,
, . 台体体积公式:
. 台体体积公式: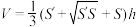 , 其中
, 其中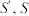 分别为台体上、下底面面积,
分别为台体上、下底面面积, 为台体高.
为台体高.
(1)证明:直线
 平面
平面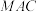 ;
;
(2)若 ,
, ,
,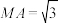 ,三棱锥
,三棱锥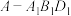 的体积
的体积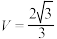 ,求 该组合体的体积.
,求 该组合体的体积. 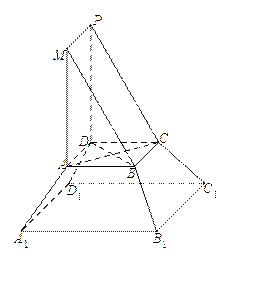
 与刍童
与刍童 的组合体中
的组合体中 ,
, . 台体体积公式:
. 台体体积公式: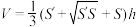 , 其中
, 其中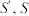 分别为台体上、下底面面积,
分别为台体上、下底面面积, 为台体高.
为台体高. (1)证明:直线

 平面
平面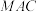 ;
; (2)若
 ,
, ,
,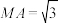 ,三棱锥
,三棱锥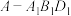 的体积
的体积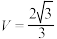 ,求 该组合体的体积.
,求 该组合体的体积. 
您最近一年使用:0次
2018-02-06更新
|
423次组卷
|
4卷引用:河南省信阳市2018-2019学年高一上学期期末数学试题



