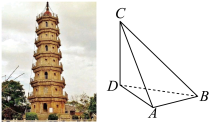
1 . 罗星塔,位于福州马尾,某校开展数学建模活动,有学生选择测量罗星塔的高度,为此,他们设计了测量方案,如图, 罗星塔垂直于水平面,他们选择了与罗星塔底部D在同一水平面上的A,B两点,测得∠ADB=45°, AB=30米,且在A,B两点观察塔顶C点,仰角分别为45°和  ,其中
,其中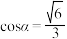 .
.
(2)在(1)的条件下求多面体A-BCD的表面积;
(3)在(1)的条件下求多面体A-BCD的内切球的半径.
 ,其中
,其中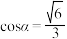 .
.
(2)在(1)的条件下求多面体A-BCD的表面积;
(3)在(1)的条件下求多面体A-BCD的内切球的半径.
您最近一年使用:0次
名校
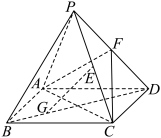
2 . 如图,在四棱锥 中,底面
中,底面 是平行四边形,
是平行四边形, 分别为
分别为 的中点,
的中点, 为线段
为线段 上一点,且
上一点,且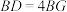 .
. 平面
平面 ;
;
(2)若四棱锥 为正四棱锥,且
为正四棱锥,且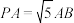 ,求四棱锥
,求四棱锥 的外接球与正四棱锥
的外接球与正四棱锥 的体积之比.
的体积之比.
 中,底面
中,底面 是平行四边形,
是平行四边形, 分别为
分别为 的中点,
的中点, 为线段
为线段 上一点,且
上一点,且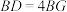 .
.
 平面
平面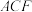 ;
;(2)若四棱锥
 为正四棱锥,且
为正四棱锥,且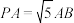 ,求四棱锥
,求四棱锥 的外接球与正四棱锥
的外接球与正四棱锥 的体积之比.
的体积之比.
您最近一年使用:0次
2024-06-17更新
|
996次组卷
|
2卷引用:福建省福州市部分学校教学联盟2023-2024学年高一下学期期末模拟考试数学试题
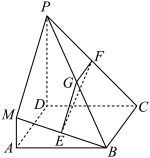
3 . 在如图所示的几何体中,底面 是正方形,四边形
是正方形,四边形 是直角梯形,
是直角梯形, ,
, ,平面
,平面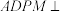 平面
平面 ,
,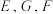 分别为
分别为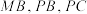 的中点,
的中点, ,
,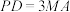 .
.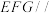 平面
平面 ;
;
(2)求多面体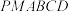 的体积.
的体积.
 是正方形,四边形
是正方形,四边形 是直角梯形,
是直角梯形, ,
, ,平面
,平面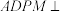 平面
平面 ,
,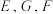 分别为
分别为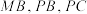 的中点,
的中点, ,
,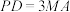 .
.
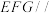 平面
平面 ;
;(2)求多面体
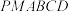 的体积.
的体积.
您最近一年使用:0次
2023-07-27更新
|
294次组卷
|
2卷引用:福建省三明市2022-2023学年高一下学期期末质量检测数学试题
名校
解题方法
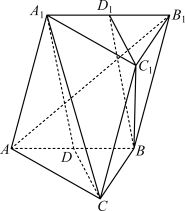
4 . 如图,斜三棱柱 中,
中, ,
, 为
为 的中点,
的中点, 为
为 的中点,平面
的中点,平面 ⊥平面
⊥平面 .
.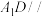 平面
平面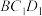 ;
;
(2)设直线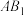 与直线
与直线 的交点为点
的交点为点 ,若三角形
,若三角形 是等边三角形且边长为2,侧棱
是等边三角形且边长为2,侧棱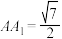 ,且异面直线
,且异面直线 与
与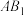 互相垂直,求异面直线
互相垂直,求异面直线 与
与 所成角;
所成角;
(3)若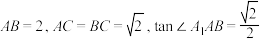 ,在三棱柱
,在三棱柱 内放置两个半径相等的球,使这两个球相切,且每个球都与三棱柱的三个侧面及一个底面相切.求三棱柱
内放置两个半径相等的球,使这两个球相切,且每个球都与三棱柱的三个侧面及一个底面相切.求三棱柱 的高.
的高.
 中,
中, ,
, 为
为 的中点,
的中点, 为
为 的中点,平面
的中点,平面 ⊥平面
⊥平面 .
.
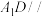 平面
平面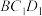 ;
;(2)设直线
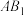 与直线
与直线 的交点为点
的交点为点 ,若三角形
,若三角形 是等边三角形且边长为2,侧棱
是等边三角形且边长为2,侧棱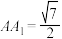 ,且异面直线
,且异面直线 与
与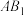 互相垂直,求异面直线
互相垂直,求异面直线 与
与 所成角;
所成角;(3)若
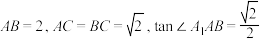 ,在三棱柱
,在三棱柱 内放置两个半径相等的球,使这两个球相切,且每个球都与三棱柱的三个侧面及一个底面相切.求三棱柱
内放置两个半径相等的球,使这两个球相切,且每个球都与三棱柱的三个侧面及一个底面相切.求三棱柱 的高.
的高.
您最近一年使用:0次
2022-11-29更新
|
4162次组卷
|
8卷引用:福建省福州市部分学校教学联盟2023-2024学年高一下学期期末模拟考试数学试题
5 . 如图,长方体 的底面
的底面 是正方形,且
是正方形,且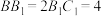 .
.
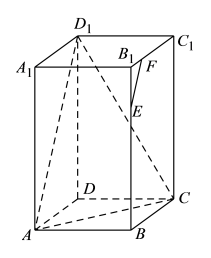
(1)求长方体 外接球的表面积;
外接球的表面积;
(2)若 、
、 分别为棱
分别为棱 、
、 上的点,且
上的点,且 ,求证:
,求证: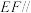 平面
平面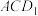 .
.
 的底面
的底面 是正方形,且
是正方形,且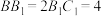 .
.
(1)求长方体
 外接球的表面积;
外接球的表面积;(2)若
 、
、 分别为棱
分别为棱 、
、 上的点,且
上的点,且 ,求证:
,求证: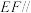 平面
平面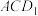 .
.
您最近一年使用:0次
解题方法
6 . 如图,在三棱柱 中,
中, ⊥
⊥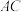 ,AB=AC=1,D是BC的中点.
,AB=AC=1,D是BC的中点. //平面
//平面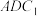 ;
;
(2)若面 ⊥面ABC,
⊥面ABC,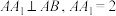 ,求几何体
,求几何体 的体积.
的体积.
 中,
中, ⊥
⊥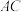 ,AB=AC=1,D是BC的中点.
,AB=AC=1,D是BC的中点.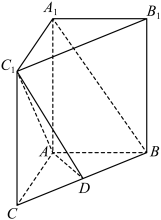
 //平面
//平面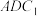 ;
;(2)若面
 ⊥面ABC,
⊥面ABC,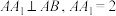 ,求几何体
,求几何体 的体积.
的体积.
您最近一年使用:0次
2021-08-04更新
|
357次组卷
|
3卷引用:福建省宁德市2020-2021学年高一下学期期末数学试题
福建省宁德市2020-2021学年高一下学期期末数学试题(已下线)高一数学下学期期末全真模拟卷(3)(必修二全部内容)-2021-2022学年高一数学考试满分全攻略(人教A版2019必修第二册)广西百色市平果市铝城中学2024-2025学年高二上学期开学收心考试数学试卷
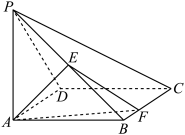
7 . 如图,在四棱锥 中,底面
中,底面 为正方形,
为正方形, 底面
底面 ,
, ,
, 为线段
为线段 的中点,
的中点, 为线段
为线段 上的动点.
上的动点.
(1)平面 与平面
与平面 是否互相垂直?如果垂直,请证明;如果不垂直,请说明理由.
是否互相垂直?如果垂直,请证明;如果不垂直,请说明理由.
(2)若 ,
, 为线段
为线段 的三等分点,求多面体
的三等分点,求多面体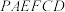 的体积.
的体积.
 中,底面
中,底面 为正方形,
为正方形, 底面
底面 ,
, ,
, 为线段
为线段 的中点,
的中点, 为线段
为线段 上的动点.
上的动点.
(1)平面
 与平面
与平面 是否互相垂直?如果垂直,请证明;如果不垂直,请说明理由.
是否互相垂直?如果垂直,请证明;如果不垂直,请说明理由.(2)若
 ,
, 为线段
为线段 的三等分点,求多面体
的三等分点,求多面体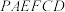 的体积.
的体积.
您最近一年使用:0次
2020-01-17更新
|
398次组卷
|
2卷引用:福建省福州市2019-2020学年高三上学期期末质量检测数学(文)试题
名校
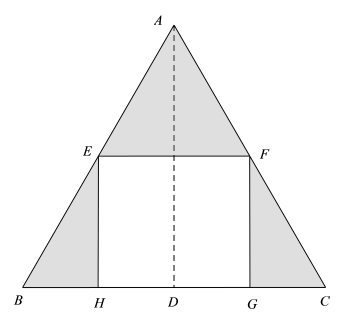
8 . 如图所示,在边长为8的正三角形ABC中,E,F依次是AB,AC的中点, ,D,H,G为垂足,若将
,D,H,G为垂足,若将 绕AD旋转
绕AD旋转 ,求阴影部分形成的几何体的表面积与体积.
,求阴影部分形成的几何体的表面积与体积.
 ,D,H,G为垂足,若将
,D,H,G为垂足,若将 绕AD旋转
绕AD旋转 ,求阴影部分形成的几何体的表面积与体积.
,求阴影部分形成的几何体的表面积与体积.
您最近一年使用:0次
2020-05-21更新
|
1940次组卷
|
15卷引用:福建省莆田市第二十五中学2019-2020学年高一上学期期末数学试题
福建省莆田市第二十五中学2019-2020学年高一上学期期末数学试题海南省海南枫叶国际学校2018-2019学年高一下学期期末数学试题【全国百强校】广东省东莞市东华中学2018-2019学年高一上学期期中考试数学试题【校级联考】湖北省部分重点中学2018-2019学年高一下学期期中考试数学试题人教B版 必修2 必杀技 第一章 1.1.6 棱柱、棱锥、棱台和球的表面积甘肃省兰州市第五十五中学2019-2020学年高一上学期12月月考数学试题人教A版(2019) 必修第二册 过关斩将 第八章 立体几何初步 本章复习提升甘肃省兰州市五十一中2018-2019学年高一下学期第一次月考数学试题人教B版(2019) 必修第四册 过关斩将 第十一章 立体几何初步 本章复习提升河北省邯郸市第一中学2019-2020学年高一下学期4月月考数学试题河北省衡水市第十三中学2019-2020学年高一下学期调研数学试题(已下线)【新教材精创】11.1.7综合复习习题课(第1课时)练习(1)辽宁省六校协作体2020-2021学年高一下学期第三次联考数学试题(已下线)13.1 基本立体图形-2020-2021学年高一数学同步课堂帮帮帮(苏教版2019必修第二册)北京市海淀区教师进修学校2021-2022学年高一6月份数学月考试题
11-12高二上·广东·期中
名校
解题方法
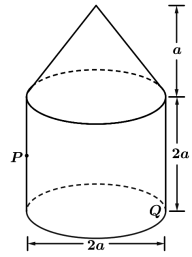
9 . 一个几何体由圆锥和圆柱组成,其尺寸如图所示.
(2)如果点 在直观图中所示位置,
在直观图中所示位置, 为所在母线中点,
为所在母线中点, 为母线与底面圆的交点,求在几何体表面上,从
为母线与底面圆的交点,求在几何体表面上,从 点到
点到 点的最短路径长.
点的最短路径长.
(2)如果点
 在直观图中所示位置,
在直观图中所示位置, 为所在母线中点,
为所在母线中点, 为母线与底面圆的交点,求在几何体表面上,从
为母线与底面圆的交点,求在几何体表面上,从 点到
点到 点的最短路径长.
点的最短路径长.
您最近一年使用:0次
2021-05-17更新
|
1653次组卷
|
34卷引用:2013-2014学年福建省晋江市季延中学高一下学期期末考试数学试卷
(已下线)2013-2014学年福建省晋江市季延中学高一下学期期末考试数学试卷2015-2016学年福建省龙海市程溪中学高一下期中数学试卷【市级联考】吉林省公主岭市2018-2019学年高二上学期期末考试数学(文)试题河南省郑州市二中2015-2016学年高一上学期期末数学试题四川省成都市温江区2019-2020学年度高一下学期期末考试数学试题吉林省长春市实验中学2019-2020学年高一下学期期末考试数学(文科)试卷吉林省长春市实验中学2019-2020学年高一下学期期末考试数学(理)试卷(已下线)2011-2012学年度广东省东山中学高二第一学期期中理科数学试卷2016-2017学年山西怀仁县一中高二理上学期期中数学试卷2016-2017学年山西怀仁县一中高二文上学期期中数学试卷北京市东城区171中学2016-2017高二上学期期中考试数学(文)试题【全国百强校】河北省邢台市第一中学2017-2018学年高一下学期第三次月考数学(文)试题【全国百强校】四川省成都市外国语学校2018-2019学年高一5月月考数学试题四川省乐山市十校2019-2020学年高二上学期期中数学(文)试题四川省乐山十校2019-2020学年高二上学期期中联考数学(理)试题甘肃省天水市甘谷一中2019-2020学年高一上学期第二次月考数学试题云南省昆明市东川区明月中学2018-2019学年高一下学期期中考试数学试题(已下线)专题8.1 空间几何体的结构及其表面积、体积-2021年高考数学(理)一轮复习-题型全归纳与高效训练突破(已下线)专题8.1 空间几何体的结构及其表面积、体积-2021年高考数学(文)一轮复习-题型全归纳与高效训练突破(已下线)专题8.2 空间几何体的表面积和体积(精练)-2021年高考数学(理)一轮复习讲练测(已下线)专题8.2 空间几何体的表面积和体积 (精练)-2021年高考数学(理)一轮复习学与练山东省泰安肥城市2020-2021学年高一下学期期中考试数学试题上海市复旦大学附属中学2021-2022学年高二上学期期中数学试题山西省运城市景胜中学2021-2022学年高二下学期4月月考数学(文)试题山西省运城市景胜中学2021-2022学年高二下学期4月月考数学(理)试题(已下线)期中模拟预测卷02(测试范围:空间向量与立体几何)-2022-2023学年高二数学上学期期中期末考点大串讲(沪教版2020必修第三册+选修一)(已下线)第09讲 空间几何体的结构与直观图(核心考点讲与练)(2)四川省乐山市草堂高级中学2022-2023学年高二上学期期中数学试题(已下线)8.1基本立体图形(第2课时圆柱、圆锥、圆台、球的结构特征简单组合体的结构特征)(精讲)(1)精讲)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)湖北省武汉市第一中学2022-2023学年高一下学期5月月考数学试题(已下线)高一数学下学期期中精选50题(基础版)-2021-2022学年高一数学考试满分全攻略(人教A版2019必修第二册)(原卷版)上海市民办新虹桥中学2023-2024学年高二上学期期中考试数学试卷河南省信阳市光山县第二高级中学2023-2024学年高一下学期4月期中考试数学试题(已下线)11.1.5 旋转体-【帮课堂】(人教B版2019必修第四册)
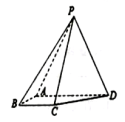
10 . 如图,四棱锥 中,侧面
中,侧面 底面
底面 ,
, ,
, ,
,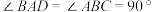 ,
,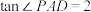 .
.
(1)证明:直线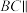 平面
平面 ;
;
(2)若四棱锥 的体积为8,求三棱锥
的体积为8,求三棱锥 的内切球的表面积.
的内切球的表面积.
 中,侧面
中,侧面 底面
底面 ,
, ,
, ,
,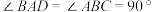 ,
,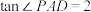 .
.(1)证明:直线
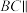 平面
平面 ;
;(2)若四棱锥
 的体积为8,求三棱锥
的体积为8,求三棱锥 的内切球的表面积.
的内切球的表面积.
您最近一年使用:0次



