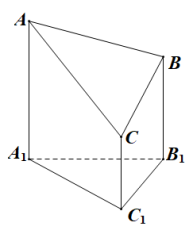
1 . 在 中,已知
中,已知 ,
, ,
, ,
, 为线段BC上一个动点.
为线段BC上一个动点.
(1)若AD为 的角平分线,求线段AD的长;
的角平分线,求线段AD的长;
(2)将 折起到
折起到 的位置,记二面角
的位置,记二面角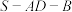 的大小为
的大小为 .
.
(i)若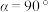 ,且AD为
,且AD为 的角平分线,求三棱锥
的角平分线,求三棱锥 外接球的面积;
外接球的面积;
(ii)若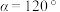 ,求三棱锥
,求三棱锥 外接球的面积最小值.
外接球的面积最小值.
 中,已知
中,已知 ,
, ,
, ,
, 为线段BC上一个动点.
为线段BC上一个动点.(1)若AD为
 的角平分线,求线段AD的长;
的角平分线,求线段AD的长;(2)将
 折起到
折起到 的位置,记二面角
的位置,记二面角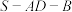 的大小为
的大小为 .
.(i)若
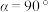 ,且AD为
,且AD为 的角平分线,求三棱锥
的角平分线,求三棱锥 外接球的面积;
外接球的面积;(ii)若
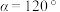 ,求三棱锥
,求三棱锥 外接球的面积最小值.
外接球的面积最小值.
您最近一年使用:0次
解题方法
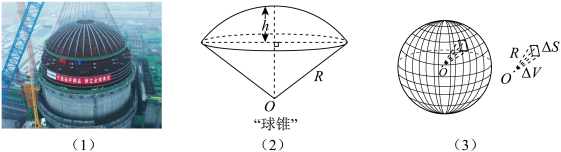
2 . 据报道,2024年4月15日,正值全民国家安全教育日,田湾核电8号机组穹顶球冠吊装成功(如图(1)),标志着国内最重核电机组薄壳钢衬里穹顶吊装工作安全完成,有力推动了我国产业结构和能源结构的调整,助力“双碳”目标顺利实现.报道中提到的球冠是一个空间几何概念,它是指球面被一个平面所截得的一部分(不包含截面),垂直于截面的直径被截得的部分是球冠的高.球冠面积等于截得它的球面上大圆(过球心的截面圆)周长与球冠的高的乘积.和球冠相对应的几何体叫球缺,它是指球体被一个平面所截得的一部分,截面是球缺的底.当球缺的高小于球半径时,我们把球缺与以球缺的底为底、以球心为顶点的圆锥所构成的体,称作“球锥”(如图(2))当一个四面体各顶点都在“球锥”表面上时,称这个四面体内接此“球锥”.如图(2),设一个“球锥”所在球的半径为 ,其中球冠高为
,其中球冠高为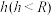 .
.
(2)在该“球锥”中,当球缺的体积与圆锥的体积相等时,求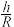 的值;
的值;
(3)已知一个棱长为 的正四面体内接此“球锥”,并且有一个顶点与球心重合,若满足条件的
的正四面体内接此“球锥”,并且有一个顶点与球心重合,若满足条件的 有且只有一个,求
有且只有一个,求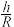 的取值范围.
的取值范围.
 ,其中球冠高为
,其中球冠高为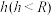 .
.
(2)在该“球锥”中,当球缺的体积与圆锥的体积相等时,求
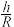 的值;
的值;(3)已知一个棱长为
 的正四面体内接此“球锥”,并且有一个顶点与球心重合,若满足条件的
的正四面体内接此“球锥”,并且有一个顶点与球心重合,若满足条件的 有且只有一个,求
有且只有一个,求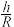 的取值范围.
的取值范围.
您最近一年使用:0次
2024-06-27更新
|
373次组卷
|
3卷引用:浙江省台州市2023-2024学年高一下学期6月期末考试数学试题
名校
3 . 如图1,在梯形 中,
中, ,
, 是线段
是线段 上的一点,
上的一点, ,
, ,将
,将 沿
沿 翻折到
翻折到 的位置.
的位置.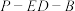 为直二面角,
为直二面角, ,
, 分别是
分别是 ,
, 的中点,若直线
的中点,若直线 与平面
与平面 所成角为
所成角为 ,
,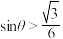 ,求平面
,求平面 与平面
与平面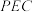 所成锐二面角的余弦值的取值范围;
所成锐二面角的余弦值的取值范围;
(2)我们把和两条异面直线都垂直相交的直线叫做两条异面直线的公垂线,点 为线段
为线段 的中点,
的中点, ,
, 分别在线段
分别在线段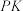 ,
, 上(不包含端点),且
上(不包含端点),且 为
为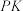 ,
, 的公垂线,如图3所示,记四面体
的公垂线,如图3所示,记四面体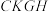 的内切球半径为
的内切球半径为 ,证明:
,证明: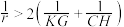 .
.
 中,
中, ,
, 是线段
是线段 上的一点,
上的一点, ,
, ,将
,将 沿
沿 翻折到
翻折到 的位置.
的位置.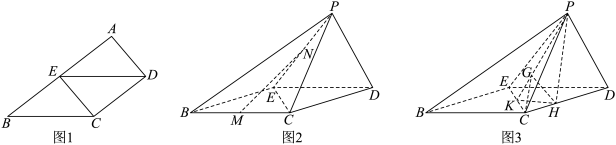
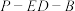 为直二面角,
为直二面角, ,
, 分别是
分别是 ,
, 的中点,若直线
的中点,若直线 与平面
与平面 所成角为
所成角为 ,
,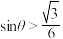 ,求平面
,求平面 与平面
与平面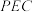 所成锐二面角的余弦值的取值范围;
所成锐二面角的余弦值的取值范围;(2)我们把和两条异面直线都垂直相交的直线叫做两条异面直线的公垂线,点
 为线段
为线段 的中点,
的中点, ,
, 分别在线段
分别在线段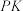 ,
, 上(不包含端点),且
上(不包含端点),且 为
为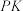 ,
, 的公垂线,如图3所示,记四面体
的公垂线,如图3所示,记四面体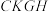 的内切球半径为
的内切球半径为 ,证明:
,证明: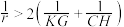 .
.
您最近一年使用:0次
2024-03-03更新
|
1174次组卷
|
3卷引用:浙江省绍兴市柯桥区2023-2024学年高一上学期期末教学质量调测数学试题
浙江省绍兴市柯桥区2023-2024学年高一上学期期末教学质量调测数学试题(已下线)第四章 立体几何解题通法 专题二 体积法 微点3 体积法综合训练【基础版】江苏省南京市第一中学2025届高三暑期阶段性测试数学试卷
20-21高一·全国·课后作业
4 . 如图,圆锥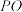 的底面直径和高均是
的底面直径和高均是 ,过
,过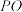 的中点
的中点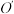 作平行于底面的截面,以该截面为底面挖去一个圆柱,求剩下几何体的表面积和体积.
作平行于底面的截面,以该截面为底面挖去一个圆柱,求剩下几何体的表面积和体积.
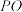 的底面直径和高均是
的底面直径和高均是 ,过
,过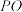 的中点
的中点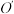 作平行于底面的截面,以该截面为底面挖去一个圆柱,求剩下几何体的表面积和体积.
作平行于底面的截面,以该截面为底面挖去一个圆柱,求剩下几何体的表面积和体积.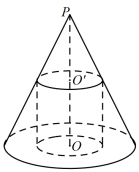
您最近一年使用:0次
2021-12-02更新
|
1302次组卷
|
6卷引用:浙江省温州市平阳县万全综合高级中学2023-2024学年高一下学期期末普高单考数学试题
浙江省温州市平阳县万全综合高级中学2023-2024学年高一下学期期末普高单考数学试题(已下线)8.3 简单几何体的表面积与体积(已下线)专题8 立体几何初步(1)陕西省西安市第六十六中学2022-2023学年高一下学期期中数学试题人教A版(2019)必修第二册课本习题 习题8.3山东省聊城一中2023-2024学年下学期期中考试高一数学试题
解题方法
5 . 已知矩形 中,
中, ,
,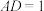 ,
, 为线段
为线段 上一点(不在端点),沿线段
上一点(不在端点),沿线段 将
将 折成
折成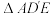 ,使得平面
,使得平面 平面
平面 .
.
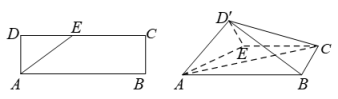
(1)证明:平面 与平面
与平面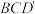 不可能垂直;
不可能垂直;
(2)若二面角 大小为60°,
大小为60°,
(ⅰ)求直线 与
与 所成角的余弦值;
所成角的余弦值;
(ⅱ)求三棱锥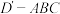 的外接球的体积.
的外接球的体积.
 中,
中, ,
,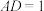 ,
, 为线段
为线段 上一点(不在端点),沿线段
上一点(不在端点),沿线段 将
将 折成
折成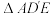 ,使得平面
,使得平面 平面
平面 .
.
(1)证明:平面
 与平面
与平面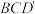 不可能垂直;
不可能垂直;(2)若二面角
 大小为60°,
大小为60°,(ⅰ)求直线
 与
与 所成角的余弦值;
所成角的余弦值;(ⅱ)求三棱锥
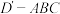 的外接球的体积.
的外接球的体积.
您最近一年使用:0次
6 . 如图①,在正方体ABCD-A1B1C1D1中,E,F,G分别为AB,BC,BB1,的中点.
(2)将该正方体截去八个与四面体B-EFG相同的四面体得到一个多面体(如图②),若该多面体的体积是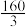 ,求该正方体的棱长.
,求该正方体的棱长.
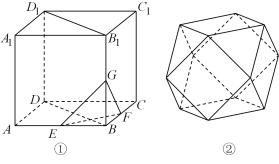
(2)将该正方体截去八个与四面体B-EFG相同的四面体得到一个多面体(如图②),若该多面体的体积是
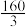 ,求该正方体的棱长.
,求该正方体的棱长.
您最近一年使用:0次
2021-08-07更新
|
484次组卷
|
3卷引用:浙江省宁波市余姚市2022-2023学年高一下学期期末数学试题
7 . 如图在直角梯形 中,
中, ,
,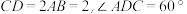 ,该梯形绕着直线
,该梯形绕着直线 旋转一周.
旋转一周.
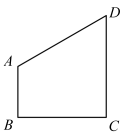
(1)求所形成的封闭几何体的体积;
(2)求所形成的封闭几何体的表面积.
 中,
中, ,
,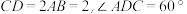 ,该梯形绕着直线
,该梯形绕着直线 旋转一周.
旋转一周.
(1)求所形成的封闭几何体的体积;
(2)求所形成的封闭几何体的表面积.
您最近一年使用:0次
20-21高一下·浙江·期末
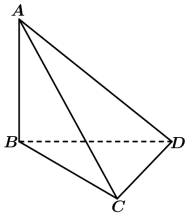
8 . 如图,在三棱锥 中,已知
中,已知 平面
平面 ,
, ,直线
,直线 与平面
与平面 所成的角为
所成的角为 .
.
(1)求证:平面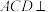 平面
平面 ;
;
(2)若三棱锥 的体积为3,求直线
的体积为3,求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)若 的外接圆面积为
的外接圆面积为 ,求三棱锥
,求三棱锥 的外接球的体积.
的外接球的体积.
 中,已知
中,已知 平面
平面 ,
, ,直线
,直线 与平面
与平面 所成的角为
所成的角为 .
.
(1)求证:平面
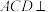 平面
平面 ;
;(2)若三棱锥
 的体积为3,求直线
的体积为3,求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;(3)若
 的外接圆面积为
的外接圆面积为 ,求三棱锥
,求三棱锥 的外接球的体积.
的外接球的体积.
您最近一年使用:0次
20-21高一下·浙江·期末
名校
9 . 如图,在棱长为 的正方体
的正方体 中,
中, 点是
点是 的中点.
的中点.
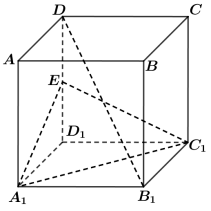
(1)证明: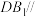 平面
平面 ;
;
(2)求三棱锥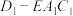 外接球的表面积.
外接球的表面积.
 的正方体
的正方体 中,
中, 点是
点是 的中点.
的中点.
(1)证明:
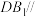 平面
平面 ;
; (2)求三棱锥
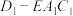 外接球的表面积.
外接球的表面积.
您最近一年使用:0次
2021-06-03更新
|
1407次组卷
|
3卷引用:【新东方】高中数学20210527-021【2021】【高一下】
(已下线)【新东方】高中数学20210527-021【2021】【高一下】新疆维吾尔自治区2022-2023学年高一下学期期末考试数学试题山西省阳泉市第一中学校2023-2024学年高二上学期开学分班数学试题

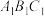 为底面的直三棱柱被一平面所截得到的几何体,截面为
为底面的直三棱柱被一平面所截得到的几何体,截面为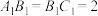 ,
,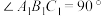 ,
,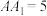 ,
,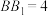 ,
,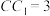 ,求:
,求: