1 . 如图,在四棱锥 中,底面
中,底面 为菱形,
为菱形,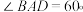 ,
, ,
, 为
为 的中点.
的中点. 平面
平面 ;
;
(2)若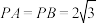 ,
,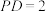 .
.
①求二面角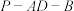 的余弦值;
的余弦值;
②求直线 与平面
与平面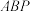 所成角的正弦值.
所成角的正弦值.
 中,底面
中,底面 为菱形,
为菱形,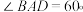 ,
, ,
, 为
为 的中点.
的中点.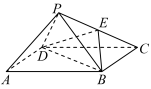
 平面
平面 ;
;(2)若
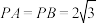 ,
,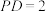 .
.①求二面角
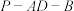 的余弦值;
的余弦值;②求直线
 与平面
与平面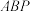 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
名校
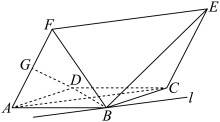
2 . 如图,已知四边形 为菱形,四边形
为菱形,四边形 为平行四边形,且
为平行四边形,且 ,
,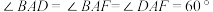 .
. 平面
平面 ;
;
(2)设平面 平面
平面 ,且二面角
,且二面角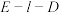 的平面角为
的平面角为 ,
,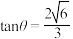 , 设
, 设 为线段
为线段 的中点,求
的中点,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 为菱形,四边形
为菱形,四边形 为平行四边形,且
为平行四边形,且 ,
,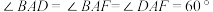 .
.
 平面
平面 ;
;(2)设平面
 平面
平面 ,且二面角
,且二面角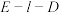 的平面角为
的平面角为 ,
,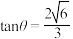 , 设
, 设 为线段
为线段 的中点,求
的中点,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2024-07-22更新
|
778次组卷
|
3卷引用:辽宁省大连市育明高中2023-2024学年高一下学期期末考试数学试卷
名校
3 . 如图在四棱锥 中,底面
中,底面 为矩形,侧棱
为矩形,侧棱 ,且
,且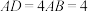 ,
, ,
,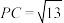 ,点E为AD中点,
,点E为AD中点, 平面
平面 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)点F为对角线AC上的点,且 ,垂足为G,求FG与平面ABCD所成的最大角的正弦值.
,垂足为G,求FG与平面ABCD所成的最大角的正弦值.
 中,底面
中,底面 为矩形,侧棱
为矩形,侧棱 ,且
,且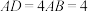 ,
, ,
,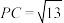 ,点E为AD中点,
,点E为AD中点,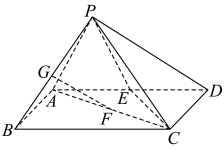
 平面
平面 ;
;(2)求二面角
 的余弦值;
的余弦值;(3)点F为对角线AC上的点,且
 ,垂足为G,求FG与平面ABCD所成的最大角的正弦值.
,垂足为G,求FG与平面ABCD所成的最大角的正弦值.
您最近一年使用:0次
2024-06-23更新
|
860次组卷
|
4卷引用:辽宁省大连市育明高中2023-2024学年高一下学期期末考试数学试卷
辽宁省大连市育明高中2023-2024学年高一下学期期末考试数学试卷浙东北联盟(ZDB)四校2023-2024学年高一下学期期中考试数学试卷(已下线)第3套 全真模拟卷 (中等)【高一期末复习全真模拟】河南省信阳市息县第二高级中学联考2023-2024学年高一下学期7月期末考试数学试题
4 . 已知三棱锥 的棱
的棱 、
、 、
、 两两垂直,
两两垂直,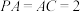 ,
, ,
, 为
为 的中点,
的中点, 在棱
在棱 上,且
上,且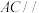 平面
平面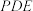 ,则下列说法错误的是( ).
,则下列说法错误的是( ).
 的棱
的棱 、
、 、
、 两两垂直,
两两垂直,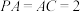 ,
, ,
, 为
为 的中点,
的中点, 在棱
在棱 上,且
上,且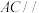 平面
平面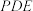 ,则下列说法错误的是( ).
,则下列说法错误的是( ).A.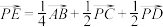 |
B. 与平面 与平面 所成的角为 所成的角为 |
C.三棱锥 外接球的表面积为 外接球的表面积为 |
D.点 到平面 到平面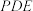 的距离为 的距离为 |
您最近一年使用:0次
解题方法
5 . 在正三棱台 中,
中, ,
,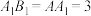 ,
, 为
为 中点,
中点, 在
在 上,
上, .
. 与平面
与平面 的交点
的交点 ,并写出
,并写出 与
与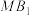 的比值(在图中保留作图痕迹,不必写出画法和理由);
的比值(在图中保留作图痕迹,不必写出画法和理由);
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中, ,
,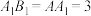 ,
, 为
为 中点,
中点, 在
在 上,
上, .
.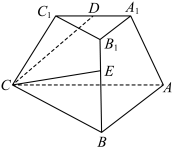
 与平面
与平面 的交点
的交点 ,并写出
,并写出 与
与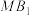 的比值(在图中保留作图痕迹,不必写出画法和理由);
的比值(在图中保留作图痕迹,不必写出画法和理由);(2)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2023-08-02更新
|
1724次组卷
|
6卷引用:辽宁省大连市2022-2023学年高一下学期期末数学试题
辽宁省大连市2022-2023学年高一下学期期末数学试题广东省阳江市2024届高三上学期开学适应性考试数学试题(已下线)重难点突破02 利用传统方法求线线角、线面角、二面角与距离(四大题型)(已下线)第八章 立体几何初步(压轴题专练)-单元速记·巧练(人教A版2019必修第二册)(已下线)重难点专题13 轻松搞定线面角问题-【帮课堂】(苏教版2019必修第二册)(已下线)专题02 高一下期末真题精选(2)-期末考点大串讲(人教A版2019必修第二册)
名校
6 . 正四面体ABCD中异面直线AB与CD所成角为 ,侧棱AB与底面BCD所成角为
,侧棱AB与底面BCD所成角为 ,侧面ABC与底面BCD所成的锐二面角为
,侧面ABC与底面BCD所成的锐二面角为 ,则( )
,则( )
 ,侧棱AB与底面BCD所成角为
,侧棱AB与底面BCD所成角为 ,侧面ABC与底面BCD所成的锐二面角为
,侧面ABC与底面BCD所成的锐二面角为 ,则( )
,则( )A.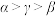 | B. | C.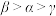 | D.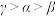 |
您最近一年使用:0次
2023-07-06更新
|
955次组卷
|
4卷引用:辽宁省大连市第八中学2023-2024学年高二上学期期中考试数学试题
辽宁省大连市第八中学2023-2024学年高二上学期期中考试数学试题江苏省常州高级中学2022-2023学年高一下学期期末数学试题(已下线)江苏省高一下学期期末真题必刷 -期末考点大串讲(苏教版(2019))江苏省扬州市扬州大学附属中学东部分校2023-2024学年高一下学期第二次模块学习效果调查数学试题
名校
7 . 如图1,在边长为4的菱形ABCD中,∠DAB=60°,点M,N分别是边BC,CD的中点,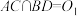 ,
,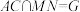 .沿MN将
.沿MN将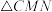 翻折到
翻折到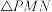 的位置,连接PA,PB,PD,得到如图2所示的五棱锥P-ABMND.
的位置,连接PA,PB,PD,得到如图2所示的五棱锥P-ABMND.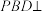 平面PAG?证明你的结论;
平面PAG?证明你的结论;
(2)当四棱锥P-MNDB体积最大时,求直线PB和平面MNDB所成角的正弦值;
(3)在(2)的条件下,在线段PA上是否存在一点Q,使得二面角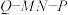 的平面角的余弦值为
的平面角的余弦值为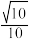 ?若存在,试确定点Q的位置;若不存在,请说明理由.
?若存在,试确定点Q的位置;若不存在,请说明理由.
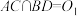 ,
,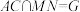 .沿MN将
.沿MN将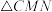 翻折到
翻折到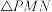 的位置,连接PA,PB,PD,得到如图2所示的五棱锥P-ABMND.
的位置,连接PA,PB,PD,得到如图2所示的五棱锥P-ABMND.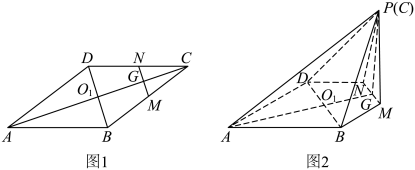
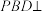 平面PAG?证明你的结论;
平面PAG?证明你的结论;(2)当四棱锥P-MNDB体积最大时,求直线PB和平面MNDB所成角的正弦值;
(3)在(2)的条件下,在线段PA上是否存在一点Q,使得二面角
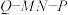 的平面角的余弦值为
的平面角的余弦值为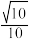 ?若存在,试确定点Q的位置;若不存在,请说明理由.
?若存在,试确定点Q的位置;若不存在,请说明理由.
您最近一年使用:0次
2022-10-21更新
|
2087次组卷
|
16卷引用:辽宁省大连市滨城联盟2022-2023学年高三上学期期中(Ⅰ)考试数学试题
辽宁省大连市滨城联盟2022-2023学年高三上学期期中(Ⅰ)考试数学试题四川省成都市第七中学2023届高三上学期零诊模拟检测理科数学试题四川省成都市第七中学2023届高三上学期零诊模拟检测理科数学试题(已下线)专题24 立体几何解答题最全归纳总结-1(已下线)第06讲 向量法求空间角(含探索性问题) (练)(已下线)1.2.4 二面角上海市七宝中学2022-2023学年高二上学期开学考数学试题四川省遂宁市射洪中学校2022-2023学年高二上学期第一次学月考试数学(理科)试题(已下线)专题03 空间向量及其应用(11个考点)【知识梳理+解题方法+专题过关】-2022-2023学年高二数学上学期期中期末考点大串讲(沪教版2020必修第三册+选修一)(已下线)3.4 空间向量在立体几何中的应用(作业)(夯实基础+能力提升)-【教材配套课件+作业】2022-2023学年高二数学精品教学课件(沪教版2020选修第一册)(已下线)数学(新高考Ⅰ卷B卷)(已下线)专题8-2 立体几何中的角和距离问题(含探索性问题)-2(已下线)上海市华东师范大学第二附属中学2023-2024学年高二上学期数学期末考试试卷上海市华东师范大学第二附属中学2023-2024学年高二上学期期末考试数学试卷(已下线)第三章 折叠、旋转与展开 专题一 平面图形的翻折、旋转 微点5 翻折、旋转问题中的最值(二)(已下线)专题07 空间向量与立体几何(九大题型+优选提升题)-【好题汇编】备战2023-2024学年高二数学下学期期末真题分类汇编(沪教版2020选择性必修,上海专用)
名校
8 . 如图1,在边长为4的菱形 中,
中,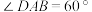 ,点
,点 ,
, 分别是边
分别是边 ,
, 的中点,
的中点, ,
,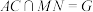 .沿
.沿 将
将 翻折到
翻折到 的位置,连接
的位置,连接 ,
, ,
, ,得到如图2所示的五棱锥
,得到如图2所示的五棱锥 .
.
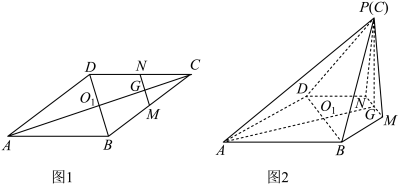
(1)在翻折过程中是否总有平面 平面
平面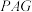 ?证明你的结论;
?证明你的结论;
(2)当四棱锥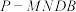 体积最大时,求直线
体积最大时,求直线 和平面
和平面 所成角的正弦值;
所成角的正弦值;
(3)在(2)的条件下,在线段 上是否存在一点
上是否存在一点 ,使得平面
,使得平面 与平面
与平面 所成角的余弦值为
所成角的余弦值为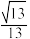 ?若存在,试确定点
?若存在,试确定点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
 中,
中,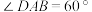 ,点
,点 ,
, 分别是边
分别是边 ,
, 的中点,
的中点, ,
,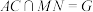 .沿
.沿 将
将 翻折到
翻折到 的位置,连接
的位置,连接 ,
, ,
, ,得到如图2所示的五棱锥
,得到如图2所示的五棱锥 .
.
(1)在翻折过程中是否总有平面
 平面
平面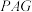 ?证明你的结论;
?证明你的结论;(2)当四棱锥
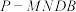 体积最大时,求直线
体积最大时,求直线 和平面
和平面 所成角的正弦值;
所成角的正弦值;(3)在(2)的条件下,在线段
 上是否存在一点
上是否存在一点 ,使得平面
,使得平面 与平面
与平面 所成角的余弦值为
所成角的余弦值为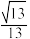 ?若存在,试确定点
?若存在,试确定点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
您最近一年使用:0次
2022-11-20更新
|
597次组卷
|
2卷引用:辽宁省大连市滨城高中联盟2022-2023学年高二上学期期中考试数学试题
名校
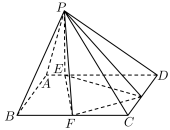
9 . 如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形, ,
,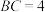 ,已知
,已知 ,且
,且 平面
平面 ,
,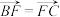 ,
,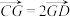 .
.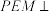 平面PFG,并说明理由;
平面PFG,并说明理由;
(2)若二面角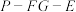 的余弦值为
的余弦值为 ,求PG与平面PEM所成角的正切值.
,求PG与平面PEM所成角的正切值.
 中,底面
中,底面 是矩形,
是矩形, ,
,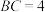 ,已知
,已知 ,且
,且 平面
平面 ,
,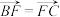 ,
,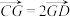 .
.
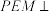 平面PFG,并说明理由;
平面PFG,并说明理由;(2)若二面角
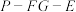 的余弦值为
的余弦值为 ,求PG与平面PEM所成角的正切值.
,求PG与平面PEM所成角的正切值.
您最近一年使用:0次
2022-07-21更新
|
1070次组卷
|
5卷引用:辽宁省大连市第三十六中学2022-2023学年高一下学期6月月考数学试题
辽宁省大连市第三十六中学2022-2023学年高一下学期6月月考数学试题辽宁省葫芦岛市2021-2022学年高一下学期期末数学试题(已下线)专题强化训练四 直线与平面所成的角、二面角的平面角的常见解法(1)-《考点·题型·技巧》(已下线)第03讲 空间中平行、垂直问题10种常见考法归类(2)(已下线)11.4.2 平面与平面垂直-【帮课堂】(人教B版2019必修第四册)
10 . 如图,在四棱锥 中,
中,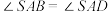
 ,底面
,底面 为正方形.记直线
为正方形.记直线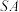 与平面
与平面 所成的角为
所成的角为 .
.
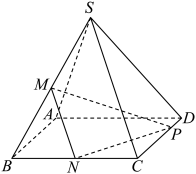
(1)求证:平面 平面
平面 ;
;
(2)若二面角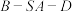 的大小为
的大小为 ,求
,求 的值;
的值;
(3)当 时,
时,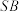 、
、 中点为
中点为 ,
, ,点
,点 为线段
为线段 上的动点(包括端点),
上的动点(包括端点),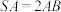 ,二面角
,二面角 的大小记为
的大小记为 ,求
,求 的取值范围.
的取值范围.
 中,
中,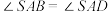
 ,底面
,底面 为正方形.记直线
为正方形.记直线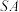 与平面
与平面 所成的角为
所成的角为 .
.
(1)求证:平面
 平面
平面 ;
;(2)若二面角
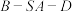 的大小为
的大小为 ,求
,求 的值;
的值;(3)当
 时,
时,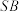 、
、 中点为
中点为 ,
, ,点
,点 为线段
为线段 上的动点(包括端点),
上的动点(包括端点),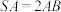 ,二面角
,二面角 的大小记为
的大小记为 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2022-07-20更新
|
1389次组卷
|
2卷引用:辽宁省大连市2021-2022学年高一下学期期末数学试题



