名校
解题方法
1 . 在平面直角坐标系 中,点
中,点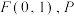 为动点,以
为动点,以 为直径的圆与
为直径的圆与 轴相切,记
轴相切,记 的轨迹为
的轨迹为 .
.
(1)求 的方程;
的方程;
(2)设 为直线
为直线 上的动点,过
上的动点,过 的直线与
的直线与 相切于点
相切于点 ,过
,过 作直线
作直线 的垂线交
的垂线交 于点
于点 ,求
,求 面积的最小值.
面积的最小值.
 中,点
中,点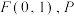 为动点,以
为动点,以 为直径的圆与
为直径的圆与 轴相切,记
轴相切,记 的轨迹为
的轨迹为 .
.(1)求
 的方程;
的方程;(2)设
 为直线
为直线 上的动点,过
上的动点,过 的直线与
的直线与 相切于点
相切于点 ,过
,过 作直线
作直线 的垂线交
的垂线交 于点
于点 ,求
,求 面积的最小值.
面积的最小值.
您最近一年使用:0次
2024-02-24更新
|
2413次组卷
|
7卷引用:黑龙江省齐齐哈尔市2024届高三第一次模拟考试数学试题
黑龙江省齐齐哈尔市2024届高三第一次模拟考试数学试题(已下线)第四套 最新模拟复盘卷(已下线)专题07 直线与圆、圆锥曲线(已下线)信息必刷卷05山西省怀仁市第一中学校2023-2024学年高三下学期第三次模拟考试数学试题(已下线)信息必刷卷04(江苏专用,2024新题型)江苏省盐城市2023-2024学年高二下学期5月月考数学试题
解题方法
2 . 已知四面体 的各个面均为全等的等腰三角形,且
的各个面均为全等的等腰三角形,且 .设
.设 为空间内任一点,且
为空间内任一点,且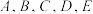 五点在同一个球面上,则( )
五点在同一个球面上,则( )
 的各个面均为全等的等腰三角形,且
的各个面均为全等的等腰三角形,且 .设
.设 为空间内任一点,且
为空间内任一点,且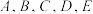 五点在同一个球面上,则( )
五点在同一个球面上,则( )A. |
B.四面体 的体积为 的体积为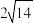 |
C.当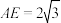 时,点 时,点 的轨迹长度为 的轨迹长度为 |
D.当三棱锥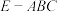 的体积为 的体积为 时,点 时,点 的轨迹长度为 的轨迹长度为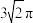 |
您最近一年使用:0次
2024-02-24更新
|
2768次组卷
|
7卷引用:黑龙江省齐齐哈尔市2024届高三第一次模拟考试数学试题
黑龙江省齐齐哈尔市2024届高三第一次模拟考试数学试题(已下线)第1套 复盘提升卷(模块二 2月开学)(已下线)黄金卷06(2024新题型)(已下线)专题04 立体几何(已下线)压轴小题7 探究立体几何中的动态问题(已下线)第20题 立体几何中的轨迹问题(高三二轮每日一题)广西梧州市、忻城县2024届高中毕业班5月仿真考试数学试卷
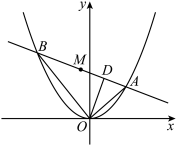
3 . 如图,已知直线与抛物线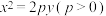 交于A,B两点,且
交于A,B两点,且 ,
, 于点D,点M为弦AB的中点,则下列说法正确的是( )
于点D,点M为弦AB的中点,则下列说法正确的是( )
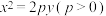 交于A,B两点,且
交于A,B两点,且 ,
, 于点D,点M为弦AB的中点,则下列说法正确的是( )
于点D,点M为弦AB的中点,则下列说法正确的是( )
A.A,B两点的横坐标之积为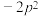 | B.当点D的坐标为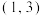 时, 时,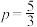 |
C.直线AB过定点 | D.点M的轨迹方程为 |
您最近一年使用:0次
2023-07-28更新
|
476次组卷
|
3卷引用:黑龙江省齐齐哈尔市讷河市第二中学等3校2022-2023学年高二下学期开学考试数学试题
黑龙江省齐齐哈尔市讷河市第二中学等3校2022-2023学年高二下学期开学考试数学试题黑龙江省齐齐哈尔市克东县第一中学等2校2022-2023学年高二下学期开学考试数学试题(已下线)专题08 抛物线的压轴题(5类题型+过关检测)-【常考压轴题】2023-2024学年高二数学上学期压轴题攻略(人教A版2019选择性必修第一册)
4 . 表面积为36π的球M表面上有A,B两点,且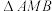 为等边三角形,空间中的动点P满足
为等边三角形,空间中的动点P满足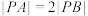 ,当点P在
,当点P在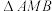 所在的平面内运动时,点P的轨迹是
所在的平面内运动时,点P的轨迹是______ ;当P在该球的球面上运动时,点P的轨迹长度为______ .
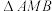 为等边三角形,空间中的动点P满足
为等边三角形,空间中的动点P满足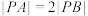 ,当点P在
,当点P在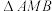 所在的平面内运动时,点P的轨迹是
所在的平面内运动时,点P的轨迹是
您最近一年使用:0次
名校
解题方法
5 . 已知正四棱柱 的体积为16,
的体积为16, 是棱
是棱 的中点,
的中点, 是侧棱
是侧棱 上的动点,直线
上的动点,直线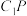 交平面
交平面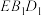 于点
于点 ,则动点
,则动点 的轨迹长度的最小值为
的轨迹长度的最小值为______ .
 的体积为16,
的体积为16, 是棱
是棱 的中点,
的中点, 是侧棱
是侧棱 上的动点,直线
上的动点,直线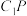 交平面
交平面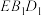 于点
于点 ,则动点
,则动点 的轨迹长度的最小值为
的轨迹长度的最小值为
您最近一年使用:0次
2023-03-24更新
|
2433次组卷
|
11卷引用:黑龙江省齐齐哈尔市龙西北高中名校联盟2023-2024学年高三上学期期末联合考试数学试题
黑龙江省齐齐哈尔市龙西北高中名校联盟2023-2024学年高三上学期期末联合考试数学试题山东省聊城市2023届高三下学期第一次模拟数学试题山东省聊城市2023届高三一模数学试题专题19平面解析几何(填空题)(已下线)重难点突破04 立体几何中的轨迹问题(六大题型)山西省吕梁市孝义市部分学校2024届高三上学期12月月考数学试题山西省晋中市灵石县第一中学校2024届高三上学期12月月考数学试题(已下线)空间几何体专题10空间中点线面的位置关系(已下线)第三章 空间轨迹问题 专题六 立体几何轨迹中的范围、最值问题 微点1 立体几何轨迹中的范围、最值问题【培优版】四川省泸州市泸县第五中学2023-2024学年高一下学期6月月考数学试题
名校
解题方法
6 . 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马 中,侧棱
中,侧棱 底面
底面 ,且
,且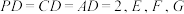 分别为
分别为 的中点,则( )
的中点,则( )
 中,侧棱
中,侧棱 底面
底面 ,且
,且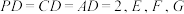 分别为
分别为 的中点,则( )
的中点,则( )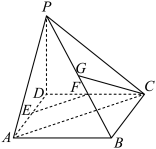
A.若 的中点为M,则四面体 的中点为M,则四面体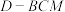 是鳖臑 是鳖臑 |
B.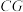 与 与 所成角的余弦值是 所成角的余弦值是 |
C.点S是平面 内的动点,若 内的动点,若 ,则动点S的轨迹是圆 ,则动点S的轨迹是圆 |
D.过点E,F,G的平面与四棱锥 表面交线的周长是 表面交线的周长是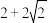 |
您最近一年使用:0次
2022-11-29更新
|
854次组卷
|
4卷引用:黑龙江省齐齐哈尔市2023-2024学年高二上学期10月期中数学试题
7 . 古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点 的距离之比为定值
的距离之比为定值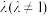 的点的轨迹是圆”. 后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.在平面直角坐标系
的点的轨迹是圆”. 后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.在平面直角坐标系 中,
中,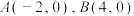 ,点P满足
,点P满足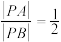 .设点P的轨迹为C,下列结论正确的是( )
.设点P的轨迹为C,下列结论正确的是( )
 的距离之比为定值
的距离之比为定值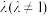 的点的轨迹是圆”. 后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.在平面直角坐标系
的点的轨迹是圆”. 后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.在平面直角坐标系 中,
中,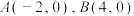 ,点P满足
,点P满足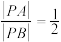 .设点P的轨迹为C,下列结论正确的是( )
.设点P的轨迹为C,下列结论正确的是( )A.C的方程为 |
B.在x轴上存在异于 的两定点 的两定点 ,使得 ,使得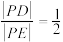 |
C.当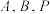 三点不共线时,射线 三点不共线时,射线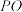 是 是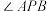 的平分线 的平分线 |
D.在C上存在点M,使得 |
您最近一年使用:0次
2023-11-03更新
|
886次组卷
|
78卷引用:黑龙江省齐齐哈尔市实验中学2021-2022学年高二上学期期中数学试题
黑龙江省齐齐哈尔市实验中学2021-2022学年高二上学期期中数学试题福建省厦门市2018-2019学年度第二学期高一年级期末数学试题(已下线)第05练—2020年新高考数学小题冲刺卷(山东专用)-《2020年新高考政策解读与配套资源》(已下线)专题15 平面解析几何(1)-2020年新高考新题型多项选择题专项训练山东省肥城一中2019-2020学年高三3月月考在线数学试题(已下线)第二十篇直线与圆02—2020年高考数学选填题专项测试(文理通用)甘肃省白银市第一中学2020届高三5月模拟考试数学(文科)试题人教B版(2019) 选择性必修第一册 必杀技 第二章 平面解析几何 素养检测江苏省苏州市高新区第一中学2020-2021学年高二上学期期初数学试题(已下线)强化卷03(4月)-冲刺2020高考数学之拿高分题目强化卷(山东专版)辽宁省六校协作体2020-2021学年高二上学期期中联考数学试题(已下线)专题08 圆的方程-2020-2021学年高中数学新教材人教A版选择性必修配套提升训练(已下线)专题13 直线与圆的方程(客观题)-2021年高考数学二轮复习热点题型精选精练(新高考地区专用)(已下线)专题11 直线与圆 -备战2021年新高考数学纠错笔记 (已下线)THUSSAT2020-2021学年高三上学期1月诊断性测试新高考数学试题(已下线)押第6题 直线与圆的方程-备战2021年高考数学(理)临考题号押题(全国卷2)(已下线)押第8题 直线与圆的方程-备战2021年高考数学(文)临考题号押题(全国卷2)江苏省2021届高三高考数学全真模拟试题(一)(已下线)黄金卷05-【赢在高考·黄金20卷】备战2021年高考数学全真模拟卷(江苏专用)(已下线)黄金卷08-【赢在高考·黄金20卷】备战2021年高考数学全真模拟卷(江苏专用)江苏省南京市第十三中学2020-2021学年高二下学期开学考试数学试题(已下线)2021年秋季高三数学开学摸底考试卷01(江苏专用)苏教版(2019) 选修第一册 突围者 第2章 专项拓展训练2 与圆有关的定点、定值、探索性问题北师大版(2019) 选修第一册 突围者 第一章 全章综合检测(已下线)第二章 圆与方程B卷(综合培优)-【双基双测】2021-2022学年高二数学同步单元AB卷(苏教版2019选择性必修第一册)(已下线)2.4 圆的方程-2021-2022学年高二数学同步速效提升练(人教A版2019选择性必修第一册)【学科网名师堂】(已下线)阶段测试一 直线与圆(基础卷)-2021-2022学年高二数学同步单元测试定心卷(苏教版2019选择性必修第一册)(已下线)2.3 圆与圆的位置关系(课堂培优)-2021-2022学年高二数学课后培优练(苏教版2019选择性必修第一册)苏教版(2019) 选修第一册 一蹴而就 第2章 单元测试江苏省常州二中2021-2022学年高二10月份调研数学试题(已下线)专题五 圆与方程-2021-2022学年高二数学同步单元AB卷(人教A版2019选择性必修第一册)(已下线)2.4 圆的方程-2021-2022学年高二数学尖子生同步培优题典(人教A版2019选择性必修第一册)福建省福州第一中学2021-2022学年高二上学期期中考试数学试题福建省福清西山学校2021-2022学年高二12月月考数学试题(已下线)综合复习与测试培优练习(卷二)-【提升专练】2021-2022学年高二数学新教材同步学案+课时对点练(苏教版2019选择性必修第一册)(已下线)专题24 《圆与方程》中的定值问题-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)重庆市万州第二高级中学2021-2022学年高二下学期入学考试数学试题(已下线)热点09 解析几何-2022年高考数学【热点·重点·难点】专练(新高考专用)(已下线)第二章 圆与方程(提分小卷)-【单元测试】2021-2022学年高二数学尖子生选拔卷(苏教版2019选择性必修第一册)(已下线)专题14 直线与圆-2022年高考数学毕业班二轮热点题型归纳与变式演练(新高考专用)(已下线)第二章 直线和圆的方程单元检测卷(知识达标卷)-【一堂好课】2021-2022学年高二数学上学期同步精品课堂(人教A版2019选择性必修第一册)(已下线)热点10 直线与圆-2022年高考数学【热点·重点·难点】专练(全国通用)(已下线)解密17 圆与方程(分层训练)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(全国通用)(已下线)必刷卷01-2022年高考数学考前信息必刷卷(新高考地区专用)(已下线)专题12 阿波罗尼斯2023版 北师大版(2019) 选修第一册 突围者 第一章 全章综合检测直线与圆的方程中的高考新题型江苏省南通市包场高级中学2022-2023学年高三上学期暑期作业检测数学试题(已下线)2.1 圆的方程(3)(已下线)第2章 圆与方程(A卷·知识通关练)(1)(已下线)专题9-2 圆的综合题型归类-1山东省青岛市青岛第二中学2022-2023学年高三上学期期末数学试题(已下线)山东省青岛第二中学2022-2023学年高三上学期1月期末测试数学试题变式题6-10江苏省连云港市赣马高级中学2022-2023学年高二上学期第二次阶段考试数学试题江苏省镇江市句容碧桂园学校2022-2023学年高三下学期期初模拟数学试题第一章 直线和圆 单元检测卷-2022-2023学年高二上学期数学北师大版(2019)选择性必修第一册(已下线)第09讲 圆的方程(已下线)专题2.12 圆的方程-重难点题型检测-2022-2023学年高二数学举一反三系列(人教A版2019选择性必修第一册)第一章 直线与圆 综合培优卷(已下线)模块三 专题8 圆的方程 B能力卷(已下线)第三节 圆的方程 B素养提升卷(已下线)模块三 专题11 圆的方程 B能力卷(已下线)高二上学期期中【压轴60题考点专练】(选修一全部内容)(已下线)2.1 圆的方程(练习)-高二数学同步精品课堂(苏教版2019选择性必修第一册)江苏省连云港市赣榆智贤中学2023-2024学年高二上学期第一次学情检测数学试题黑龙江省伊春市第一中学2023-2024学年高二上学期10月月考数学试题 陕西省宝鸡市千阳县中学2023-2024学年高二上学期期中数学试题(已下线)第03讲 圆的方程(练习)(已下线)第04讲 直线与圆、圆与圆的位置关系(练习)广东省佛山市S7高质量发展联盟2023-2024学年高二上学期期中数学试题(已下线)2.4.2 圆的一般方程【第三练】“上好三节课,做好三套题“高中数学素养晋级之路江苏省盐城市大丰区新丰中学2023-2024学年高二上学期第二次学情调研数学试卷(已下线)模块三 专题2 小题进阶提升(3) 期末终极研习室(高二人教A版)福建省福州市福清西山学校2023-2024学年高二上学期12月月考数学试题(已下线)专题07 直线与圆(解密讲义)(已下线)专题2.3 圆与圆的位置关系(2个考点六大题型)-2023-2024学年高二数学《重难点题型·高分突破》(苏教版2019选择性必修第一册)(已下线)专题3 阿波罗尼斯圆及其应用【练】(压轴小题大全)(已下线)重组3 高二期中真题重组卷(广东卷)A基础卷
解题方法
8 . 如图,在棱长为3的正方体 中,点P是平面
中,点P是平面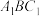 内一个动点,且满足
内一个动点,且满足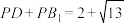 ,则点P的轨迹长度为
,则点P的轨迹长度为_____________ .
 中,点P是平面
中,点P是平面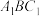 内一个动点,且满足
内一个动点,且满足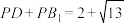 ,则点P的轨迹长度为
,则点P的轨迹长度为
您最近一年使用:0次
2022-07-21更新
|
462次组卷
|
3卷引用:黑龙江省齐齐哈尔市桃李中学2023-2024学年高一下学期期末考试数学试题
黑龙江省齐齐哈尔市桃李中学2023-2024学年高一下学期期末考试数学试题辽宁省铁岭市六校协作体2021-2022学年高一下学期期末联考数学试题(已下线)专题3.7 立体中的轨迹和截面问题-重难点突破及混淆易错规避(人教A版2019必修第二册)
9 . 阿波罗尼斯是古希腊著名的数学家,对圆锥曲线有深刻而系统的研究,阿波罗尼斯圆就是他的研究成果之一,指的是:已知动点M与两定点Q,P的距离之比 ,那么点
,那么点 的轨迹就是阿波罗尼斯圆.已知动点
的轨迹就是阿波罗尼斯圆.已知动点 的轨迹是阿波罗尼斯圆,其方程为
的轨迹是阿波罗尼斯圆,其方程为 ,定点
,定点 为
为 轴上一点,
轴上一点,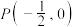 且
且 ,若点
,若点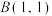 ,则
,则 的最小值为( )
的最小值为( )
 ,那么点
,那么点 的轨迹就是阿波罗尼斯圆.已知动点
的轨迹就是阿波罗尼斯圆.已知动点 的轨迹是阿波罗尼斯圆,其方程为
的轨迹是阿波罗尼斯圆,其方程为 ,定点
,定点 为
为 轴上一点,
轴上一点,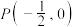 且
且 ,若点
,若点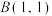 ,则
,则 的最小值为( )
的最小值为( )A. | B.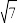 | C.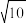 | D. |
您最近一年使用:0次
2022-08-29更新
|
3876次组卷
|
44卷引用:黑龙江省齐齐哈尔市第八中学校2023-2024学年高二上学期期中数学试题
黑龙江省齐齐哈尔市第八中学校2023-2024学年高二上学期期中数学试题湖北省部分重点中学2017-2018学年度上学期期中联考高二数学(文科)试题湖北省部分重点中学2017-2018学年度上学期期中联考高二数学理科试题重庆市三峡名校联盟高2019-2020年上学期联合考试数学试题(已下线)【新东方】新东方高二数学试卷296人教B版(2019) 选择性必修第一册 过关斩将 第二章 平面解析几何 2.1-2.3 综合拔高练江西省新余市第四中学2021届高三上学期第五次段考数学(文)试题四川省内江市第六中学2020-2021学年高二上学期第三次月考数学理科试题(已下线)考点突破12 直线和圆的方程-备战2022年高考数学一轮复习培优提升精炼(新高考地区专用)内蒙古杭锦后旗奋斗中学2020-2021学年高一下学期第二次月考数学试题云南省下关第一中学2020-2021学年高二上学期段考(一)数学(理)试题福建省厦门双十中学2021-2022学年高二上学期期中考试数学试题(已下线)江苏省南通市如皋市2021-2022学年高二上学期期中数学试题(已下线)专题08 直线方程-备战2022年高考数学学霸纠错(全国通用)(已下线)专题15 《圆与方程》中的轨迹问题(1)-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)(已下线)2020年高考浙江数学高考真题变式题6-10题2023版 北师大版(2019) 选修第一册 名师精选卷 第一章 直线与圆江苏省淮安市清江中学2022-2023学年高二上学期第一次阶段测试数学试题广东省广州市八十九中2022-2023学年高二上学期期中数学试题江西省丰城中学2023届高三(尖子班、重点班)上学期数学(文)期中复习试题河南省郑州市第十九高级中学2022-2023学年高二上学期第一次月考数学试题湖北省部分省级示范高中2022-2023学年高二上学期期中联考数学试题(已下线)专题03 圆的取值范围与最值问题题型全归纳 (1)(已下线)专题2.19 直线和圆的方程全章综合测试卷-提高篇-2022-2023学年高二数学举一反三系列(人教A版2019选择性必修第一册)2.5.2 圆的一般方程(同步练习基础版)黑龙江省鸡西实验中学2022-2023学年高二上学期期中数学试题 山东省枣庄市第八中学2023-2024学年高二上学期开学收心考试数学试题江西省宜春市宜丰县宜丰中学2022-2023学年高二下学期开学考试数学试题河南省中原名校联考2023-2024学年高二上学期9月月考数学试题河南省开封市五县联考2023-2024学年高二上学期第一次月考数学试题山东省德州市夏津育中万隆中英文高级中学2023-2024学年高二上学期9月月考数学试题山东省枣庄市第八中学2023-2024学年高二上学期10月月考数学试题(已下线)模块四 期中重组篇 专题3 期中重组卷(湖北)云南省昆明市第二十四中学2023-2024学年高二上学期10月月考数学试题安徽省铜陵市铜官区铜陵市实验高级中学2023-2024学年高二上学期11月月考数学试题江苏省镇江市镇江第一中学2024届高三上学期12月阶段测试数学试题河南省漯河市实验高级中学2024届高三上学期1月阶段模拟测试数学试题(已下线)第五篇 向量与几何 专题1 蒙日圆与阿氏圆 微点9 阿波罗尼斯圆综合训练(已下线)2.3.2 圆的一般方程(分层练习)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第一册)(已下线)大招5阿波罗尼斯圆(解题大招)(已下线)模型11 普通法求解曲线的轨迹方程问题模型 (第8章 解析几何)四川省高县中学校2023-2024学年高二上学期期中考试数学试卷(已下线)重难点突破02 活用隐圆的五种定义妙解压轴题(五大题型)云南省昆明市第三中学2024-2025学年高二上学期10月月考数学试卷



