名校
解题方法
1 . 已知椭圆C: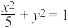 的左、右焦点分别为
的左、右焦点分别为 ,
, ,点
,点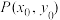 是椭圆C上异于左、右顶点的一点,则下列说法正确的是( )
是椭圆C上异于左、右顶点的一点,则下列说法正确的是( )
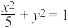 的左、右焦点分别为
的左、右焦点分别为 ,
, ,点
,点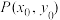 是椭圆C上异于左、右顶点的一点,则下列说法正确的是( )
是椭圆C上异于左、右顶点的一点,则下列说法正确的是( )A. 的周长为 的周长为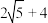 | B. 的面积的最大值为2 的面积的最大值为2 |
C.若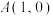 ,则 ,则 的最小值为 的最小值为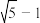 | D. 的最小值为 的最小值为 |
您最近一年使用:0次
2023-11-04更新
|
1367次组卷
|
9卷引用:吉林省四平市2023-2024学年高二上学期期中数学试题
吉林省四平市2023-2024学年高二上学期期中数学试题河北省衡水市桃城区衡水市第二中学2023-2024学年高二上学期11月期中考试数学试题江西省上饶市广信二中2023-2024学年高二上学期期中数学试题吉林省普通高中G6教考联盟2023-2024学年高二上学期1月期末考试数学试题吉林省普通高中G6教考联盟2023-2024学年高二上学期1月期末考试数学试题(B卷)黑龙江省绥化市绥棱县第一中学2023-2024学年高二上学期12月月考数学试题山东省威海市威海大光华学校2023-2024学年高二上学期11月月考数学试题广东省高州市某校2023-2024学年高二上学期期末学情数学练习卷(已下线)通关练15 椭圆11考点精练(2)
解题方法
2 . 已知如图,长为 ,宽为
,宽为 的矩形
的矩形 ,以为
,以为 焦点的椭圆
焦点的椭圆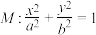 恰好过
恰好过 两点,
两点,
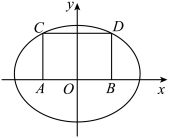
(1)求椭圆 的标准方程;
的标准方程;
(2)根据(1)所得椭圆 的标准方程,若
的标准方程,若 是椭圆
是椭圆 的左右顶点,过点
的左右顶点,过点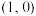 的动直线
的动直线 交椭圆
交椭圆 与
与 两点,试探究直线
两点,试探究直线 与
与 的交点是否在一定直线上,若在,请求出该直线方程,若不在,请说明理由.
的交点是否在一定直线上,若在,请求出该直线方程,若不在,请说明理由.
 ,宽为
,宽为 的矩形
的矩形 ,以为
,以为 焦点的椭圆
焦点的椭圆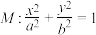 恰好过
恰好过 两点,
两点,
(1)求椭圆
 的标准方程;
的标准方程;(2)根据(1)所得椭圆
 的标准方程,若
的标准方程,若 是椭圆
是椭圆 的左右顶点,过点
的左右顶点,过点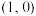 的动直线
的动直线 交椭圆
交椭圆 与
与 两点,试探究直线
两点,试探究直线 与
与 的交点是否在一定直线上,若在,请求出该直线方程,若不在,请说明理由.
的交点是否在一定直线上,若在,请求出该直线方程,若不在,请说明理由.
您最近一年使用:0次
3 . 已知动圆与圆 外切,同时与圆
外切,同时与圆 内切.
内切.
(1)求动圆圆心 的轨迹
的轨迹 的方程,并说明它是什么曲线;
的方程,并说明它是什么曲线;
(2)若直线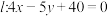 ,求曲线
,求曲线 上的点到直线
上的点到直线 的最大距离.
的最大距离.
 外切,同时与圆
外切,同时与圆 内切.
内切.(1)求动圆圆心
 的轨迹
的轨迹 的方程,并说明它是什么曲线;
的方程,并说明它是什么曲线;(2)若直线
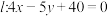 ,求曲线
,求曲线 上的点到直线
上的点到直线 的最大距离.
的最大距离.
您最近一年使用:0次
名校
4 . 已知椭圆 的一个顶点为
的一个顶点为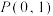 ,且离心率为
,且离心率为 .
.
(1)求椭圆C的方程;
(2)直线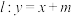 与椭圆C交于A、B两点,且
与椭圆C交于A、B两点,且 ,求m的值.
,求m的值.
 的一个顶点为
的一个顶点为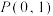 ,且离心率为
,且离心率为 .
.(1)求椭圆C的方程;
(2)直线
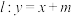 与椭圆C交于A、B两点,且
与椭圆C交于A、B两点,且 ,求m的值.
,求m的值.
您最近一年使用:0次
2022-11-08更新
|
1144次组卷
|
6卷引用:吉林省长春市长春外国语学校2022-2023学年高二下学期期中数学试题
吉林省长春市长春外国语学校2022-2023学年高二下学期期中数学试题北京市朝阳区清华大学附属中学朝阳学校2022-2023学年高二上学期期中考试数学试题(已下线)期中真题必刷椭圆60题(4个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(人教A版2019选择性必修第一册)广东省江门市第一中学中2022-2023学年高二上学期第二次段考数学试题上海外国语大学附属外国语学校2022-2023学年高二下学期3月月考数学试题天津市第五十四中学2023-2024学年高二上学期12月月考数学试题
名校
5 . 已知椭圆 过点
过点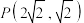 ,A、B为左右顶点,且
,A、B为左右顶点,且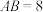 .
.
(1)求椭圆C的方程;
(2)过点A作椭圆内的圆 的两条切线,交椭圆于C、D两点,若直线CD与圆O相切,求圆O的方程;
的两条切线,交椭圆于C、D两点,若直线CD与圆O相切,求圆O的方程;
(3)过点P作(2)中圆O的两条切线,分别交椭圆于两点Q、R,求证:直线QR与圆O相切.
 过点
过点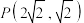 ,A、B为左右顶点,且
,A、B为左右顶点,且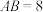 .
.(1)求椭圆C的方程;
(2)过点A作椭圆内的圆
 的两条切线,交椭圆于C、D两点,若直线CD与圆O相切,求圆O的方程;
的两条切线,交椭圆于C、D两点,若直线CD与圆O相切,求圆O的方程;(3)过点P作(2)中圆O的两条切线,分别交椭圆于两点Q、R,求证:直线QR与圆O相切.
您最近一年使用:0次
2022-09-29更新
|
854次组卷
|
3卷引用:吉林省长春市实验中学2022-2023学年高二上学期期中数学试题
6 . 已知椭圆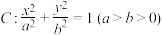 的离心率为
的离心率为 ,点
,点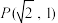 在椭圆上.
在椭圆上.
(1)求椭圆 方程;
方程;
(2)已知 为坐标原点,
为坐标原点,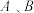 为椭圆
为椭圆 上非顶点的不同两点,且直线
上非顶点的不同两点,且直线 不过原点,不垂直于坐标轴.在下面两个条件中任选一个作为已知:①直线
不过原点,不垂直于坐标轴.在下面两个条件中任选一个作为已知:①直线 与直线
与直线 斜率之积
斜率之积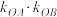 为定值
为定值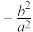 ;②
;② 的面积为定值
的面积为定值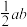 ,证明:存在常数
,证明:存在常数 ,使得
,使得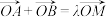 ,且点
,且点 在椭圆
在椭圆 上,并求出
上,并求出 的值.
的值.
注:如果选择两个条件分别解答,按第一个解答计分.
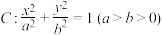 的离心率为
的离心率为 ,点
,点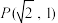 在椭圆上.
在椭圆上.(1)求椭圆
 方程;
方程;(2)已知
 为坐标原点,
为坐标原点,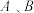 为椭圆
为椭圆 上非顶点的不同两点,且直线
上非顶点的不同两点,且直线 不过原点,不垂直于坐标轴.在下面两个条件中任选一个作为已知:①直线
不过原点,不垂直于坐标轴.在下面两个条件中任选一个作为已知:①直线 与直线
与直线 斜率之积
斜率之积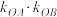 为定值
为定值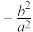 ;②
;② 的面积为定值
的面积为定值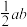 ,证明:存在常数
,证明:存在常数 ,使得
,使得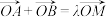 ,且点
,且点 在椭圆
在椭圆 上,并求出
上,并求出 的值.
的值.注:如果选择两个条件分别解答,按第一个解答计分.
您最近一年使用:0次
2021-11-17更新
|
934次组卷
|
4卷引用:吉林省东北师范大学附属中学2021-2022学年高二上学期期中考试数学试题
名校
解题方法
7 . 已知 ,
, 分别为椭圆
分别为椭圆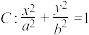
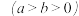 的左、右焦点,椭圆上任意一点
的左、右焦点,椭圆上任意一点 到焦点距离的最小值与最大值之比为
到焦点距离的最小值与最大值之比为 ,过
,过 且垂直于长轴的椭圆
且垂直于长轴的椭圆 的弦长为
的弦长为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)过 的直线与椭圆
的直线与椭圆 相交的交点
相交的交点 、
、 与右焦点
与右焦点 所围成的三角形的内切圆面积是否存在最大值?若存在,试求出最大值;若不存在,说明理由.
所围成的三角形的内切圆面积是否存在最大值?若存在,试求出最大值;若不存在,说明理由.
 ,
, 分别为椭圆
分别为椭圆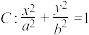
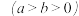 的左、右焦点,椭圆上任意一点
的左、右焦点,椭圆上任意一点 到焦点距离的最小值与最大值之比为
到焦点距离的最小值与最大值之比为 ,过
,过 且垂直于长轴的椭圆
且垂直于长轴的椭圆 的弦长为
的弦长为 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)过
 的直线与椭圆
的直线与椭圆 相交的交点
相交的交点 、
、 与右焦点
与右焦点 所围成的三角形的内切圆面积是否存在最大值?若存在,试求出最大值;若不存在,说明理由.
所围成的三角形的内切圆面积是否存在最大值?若存在,试求出最大值;若不存在,说明理由.
您最近一年使用:0次
2021-09-12更新
|
1567次组卷
|
14卷引用:吉林省白城市第一中学2021-2022学年高二上学期期中数学试题
吉林省白城市第一中学2021-2022学年高二上学期期中数学试题福建省福州屏东中学2021-2022学年高二上学期期中考试数学试题河南省顶级名校2021-2022学年高三上学期9月开学联考数学(理)试题湘豫名校联考2022届高三上学期8月数学文科试题河南省顶级名校2021-2022学年高三上学期9月开学联考数学(文)试题四川省成都市树德中学2021-2022学年高三上学期10月阶段性测试数学(文)试题四川省成都市树德中学2021-2022学年高三上学期10月阶段性测试数学(理)试题(已下线)一轮复习大题专练56—椭圆(面积最值问题1)—2022届高三数学一轮复习山西省稷山中学2021-2022学年高二上学期第二次月考数学试题(已下线)3.1.1椭圆及其标准方程(备作业)-【上好课】2021-2022学年高二数学同步备课系列(人教A版2019选择性必修第一册)河北省廊坊市第一中学2021-2022学年高一上学期12月考试数学试题(已下线)专题31 圆锥曲线存在性问题的五种类型大题100题-【千题百练】2022年新高考数学高频考点+题型专项千题百练(新高考适用)江苏省南通市如东高级中学2022-2023学年高三上学期12月阶段测试数学试题河北省2023届高三模拟数学试题
名校
解题方法
8 . 已知椭圆 过点
过点 ,椭圆的焦距为2.
,椭圆的焦距为2.
(1)求椭圆 的方程;
的方程;
(2)设直线 过点
过点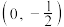 ,且斜率为
,且斜率为 ,若椭圆
,若椭圆 上存在
上存在 两点关于直线
两点关于直线 对称,
对称, 为坐标原点,求
为坐标原点,求 的取值范围及
的取值范围及 面积的最大值.
面积的最大值.
 过点
过点 ,椭圆的焦距为2.
,椭圆的焦距为2.(1)求椭圆
 的方程;
的方程;(2)设直线
 过点
过点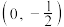 ,且斜率为
,且斜率为 ,若椭圆
,若椭圆 上存在
上存在 两点关于直线
两点关于直线 对称,
对称, 为坐标原点,求
为坐标原点,求 的取值范围及
的取值范围及 面积的最大值.
面积的最大值.
您最近一年使用:0次
2021-09-12更新
|
957次组卷
|
3卷引用:吉林省长春市朝阳区2021-2022学年高二上学期期中数学试题
吉林省长春市朝阳区2021-2022学年高二上学期期中数学试题北京市北京二中2020届高三12月份月考数学试题(已下线)专题28 圆锥曲线求范围及最值六种类型大题100题-【千题百练】2022年新高考数学高频考点+题型专项千题百练(新高考适用)
名校
解题方法
9 . 已知椭圆E: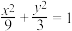 ,P为椭圆E的右顶点,O为坐标原点,过点P的直线l1,l2与椭圆E的另外一个交点分别为A,B,线段PA的中点为M,线段PB的中点为N.
,P为椭圆E的右顶点,O为坐标原点,过点P的直线l1,l2与椭圆E的另外一个交点分别为A,B,线段PA的中点为M,线段PB的中点为N.
(1)若直线OM的斜率为 ,求直线l1的方程;
,求直线l1的方程;
(2)若OM⊥ON,证明:直线AB过定点.
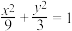 ,P为椭圆E的右顶点,O为坐标原点,过点P的直线l1,l2与椭圆E的另外一个交点分别为A,B,线段PA的中点为M,线段PB的中点为N.
,P为椭圆E的右顶点,O为坐标原点,过点P的直线l1,l2与椭圆E的另外一个交点分别为A,B,线段PA的中点为M,线段PB的中点为N.(1)若直线OM的斜率为
 ,求直线l1的方程;
,求直线l1的方程;(2)若OM⊥ON,证明:直线AB过定点.
您最近一年使用:0次
2021-08-24更新
|
577次组卷
|
3卷引用:吉林省通化市梅河口市第五中学2023-2024学年高二上学期期中数学试题
名校
10 . 若直线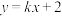 与椭圆
与椭圆 有且只有一个交点,则斜率
有且只有一个交点,则斜率 的值是
的值是_______ .
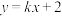 与椭圆
与椭圆 有且只有一个交点,则斜率
有且只有一个交点,则斜率 的值是
的值是
您最近一年使用:0次



