解题方法
1 . 数据传输包括发送与接收两个环节.在某数据传输中,数据是由数字0和1组成的数字串,发送时按顺序每次只发送一个数字.发送数字1时,收到的数字是1的概率为 ,收到的数字是0的概率为
,收到的数字是0的概率为 ;发送数字0时,收到的数字是0的概率为
;发送数字0时,收到的数字是0的概率为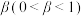 ,收到的数字是1的概率为
,收到的数字是1的概率为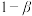 .假设每次数字的传输相互独立,且
.假设每次数字的传输相互独立,且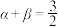 .
.
(1)当 时,若发送的数据为“10”,求收到的所有数字都正确的概率;
时,若发送的数据为“10”,求收到的所有数字都正确的概率;
(2)用 表示收到的数字串,将
表示收到的数字串,将 中数字1的个数记为
中数字1的个数记为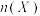 ,如
,如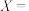 “1011”,则
“1011”,则 .
.
(ⅰ)若发送的数据为:“100”,且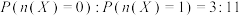 ,求
,求 ;
;
(ⅱ)若发送的数据为“1100”,求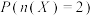 的最大值.
的最大值.
 ,收到的数字是0的概率为
,收到的数字是0的概率为 ;发送数字0时,收到的数字是0的概率为
;发送数字0时,收到的数字是0的概率为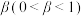 ,收到的数字是1的概率为
,收到的数字是1的概率为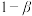 .假设每次数字的传输相互独立,且
.假设每次数字的传输相互独立,且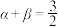 .
.(1)当
 时,若发送的数据为“10”,求收到的所有数字都正确的概率;
时,若发送的数据为“10”,求收到的所有数字都正确的概率;(2)用
 表示收到的数字串,将
表示收到的数字串,将 中数字1的个数记为
中数字1的个数记为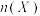 ,如
,如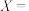 “1011”,则
“1011”,则 .
.(ⅰ)若发送的数据为:“100”,且
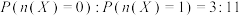 ,求
,求 ;
;(ⅱ)若发送的数据为“1100”,求
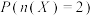 的最大值.
的最大值.
您最近一年使用:0次
名校
解题方法
2 . 将2024表示成7个正整数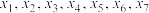 之和,得到方程
之和,得到方程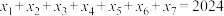 ①,称七元有序数组
①,称七元有序数组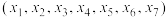 为方程①的解,对于上述的七元有序数组
为方程①的解,对于上述的七元有序数组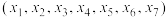 ,当
,当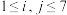 时,若
时,若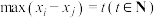 ),则称
),则称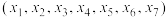 是
是 密集的一组解.
密集的一组解.
(1)方程①是否存在一组解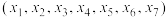 ,使得
,使得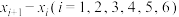 等于同一常数?
等于同一常数?
若存在,请求出该常数,若不存在,请说明理由;
(2)方程①的解中共有多少组是 密集的?
密集的?
(3)记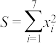 ,问S是否存在最小值?若存在,请求出S的最小值:若不存在,请说明理由.
,问S是否存在最小值?若存在,请求出S的最小值:若不存在,请说明理由.
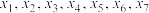 之和,得到方程
之和,得到方程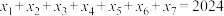 ①,称七元有序数组
①,称七元有序数组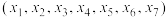 为方程①的解,对于上述的七元有序数组
为方程①的解,对于上述的七元有序数组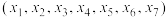 ,当
,当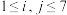 时,若
时,若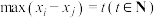 ),则称
),则称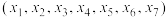 是
是 密集的一组解.
密集的一组解.(1)方程①是否存在一组解
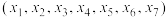 ,使得
,使得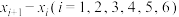 等于同一常数?
等于同一常数?若存在,请求出该常数,若不存在,请说明理由;
(2)方程①的解中共有多少组是
 密集的?
密集的?(3)记
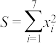 ,问S是否存在最小值?若存在,请求出S的最小值:若不存在,请说明理由.
,问S是否存在最小值?若存在,请求出S的最小值:若不存在,请说明理由.
您最近一年使用:0次
名校
解题方法
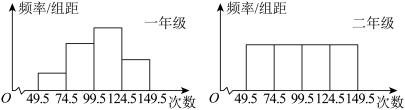
3 . 为了解学生的体能情况,抽取某学校一、二年级部分学生进行跳绳测试,将所得的数据整理后画出频率分布直方图(如图),设一年级跳绳次数为 ,二年级跳绳次数为
,二年级跳绳次数为 ,则
,则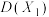
______ 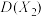 .(填“
.(填“ ”或“
”或“ ”)
”)
 ,二年级跳绳次数为
,二年级跳绳次数为 ,则
,则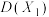
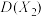 .(填“
.(填“ ”或“
”或“ ”)
”)
您最近一年使用:0次
名校
解题方法
4 . 镇海中学篮球训练营有一项三人间的传球训练.训练规则是确定一人第一次将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人,每次必须将球传出.若刚好抽到甲乙丙三个人相互做传球训练,且第1次由甲将球传出,记 次传球后球在甲手中的概率为
次传球后球在甲手中的概率为 ,
,
(1)写出 ,
, ,
, 的值;
的值;
(2)求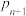 与
与 的关系式
的关系式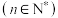 ,并求
,并求 ;
;
(3)第1次仍由甲将球传出,若首次出现连续两次球没在甲手中,则传球结束,记此时的传球次数为 ,求
,求 的期望.
的期望.
 次传球后球在甲手中的概率为
次传球后球在甲手中的概率为 ,
,
(1)写出
 ,
, ,
, 的值;
的值;(2)求
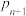 与
与 的关系式
的关系式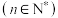 ,并求
,并求 ;
;(3)第1次仍由甲将球传出,若首次出现连续两次球没在甲手中,则传球结束,记此时的传球次数为
 ,求
,求 的期望.
的期望.
您最近一年使用:0次
名校
解题方法
5 . 如图为国家统计局发布的 年
年 月至
月至 年
年 月全国居民消费价格涨跌幅,其中同比
月全国居民消费价格涨跌幅,其中同比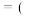 本期数
本期数 去年同期数
去年同期数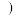
 去年同期数
去年同期数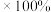 ,环比
,环比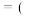 本期数
本期数 上期数
上期数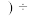 上期数
上期数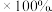 则下列说法中正确的是( )
则下列说法中正确的是( )
 年
年 月至
月至 年
年 月全国居民消费价格涨跌幅,其中同比
月全国居民消费价格涨跌幅,其中同比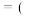 本期数
本期数 去年同期数
去年同期数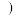
 去年同期数
去年同期数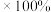 ,环比
,环比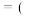 本期数
本期数 上期数
上期数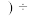 上期数
上期数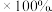 则下列说法中正确的是( )
则下列说法中正确的是( )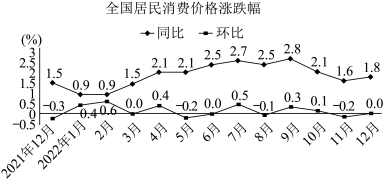
A. 年全年的全国居民消费价格比 年全年的全国居民消费价格比 年全年高 年全年高 |
B. 年 年 月至 月至 年 年 月全国居民消费价格同比的下四分位数为 月全国居民消费价格同比的下四分位数为 |
C. 年 年 月至 月至 年 年 月中, 月中, 年 年 月全国居民消费价格最高 月全国居民消费价格最高 |
D. 年 年 月比 月比 年 年 月的全国居民消费价格高 月的全国居民消费价格高 |
您最近一年使用:0次
解题方法
6 . 在去年某校高二年级“校长杯”足球比赛中,甲乙两班每场比赛平均进球数、失球数及所有场次比赛进球个数、失球个数的标准差如下表:
下列说法正确的是( )
| 进球个数平均数 | 失球个数平均数 | 进球个数标准差 | 失球个数标准差 | |
| 甲班 | 2.3 | 1.5 | 0.5 | 1.1 |
| 乙班 | 1.4 | 2.1 | 1.2 | 0.4 |
| A.甲班在防守中比乙班稳定 |
| B.乙班总体实力优于甲班 |
| C.乙班很少不失球 |
| D.乙班在进攻中有时表现很好有时表现较差 |
您最近一年使用:0次
2024高三·全国·专题练习
解题方法
7 . 将连续正整数1,2, ,
, 从小到大排列构成一个数
从小到大排列构成一个数 ,
,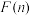 为这个数的位数
为这个数的位数 如当
如当 时,此数为123456789101112,共有15个数字,
时,此数为123456789101112,共有15个数字,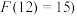 ,现从这个数中随机取一个数字,
,现从这个数中随机取一个数字, 为恰好取到0的概率.
为恰好取到0的概率.
(1)求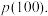
(2)当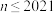 时,求
时,求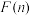 的表达式.
的表达式.
(3)令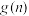 为这个数中数字0的个数,
为这个数中数字0的个数,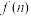 为这个数中数字9的个数,
为这个数中数字9的个数,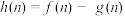 ,
,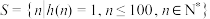 ,求当
,求当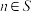 时
时 的最大值.
的最大值.
 ,
, 从小到大排列构成一个数
从小到大排列构成一个数 ,
,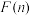 为这个数的位数
为这个数的位数 如当
如当 时,此数为123456789101112,共有15个数字,
时,此数为123456789101112,共有15个数字,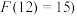 ,现从这个数中随机取一个数字,
,现从这个数中随机取一个数字, 为恰好取到0的概率.
为恰好取到0的概率.(1)求
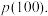
(2)当
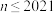 时,求
时,求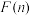 的表达式.
的表达式.(3)令
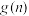 为这个数中数字0的个数,
为这个数中数字0的个数,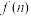 为这个数中数字9的个数,
为这个数中数字9的个数,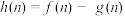 ,
,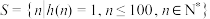 ,求当
,求当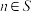 时
时 的最大值.
的最大值.
您最近一年使用:0次
解题方法
8 . 某班学生分A, ,
, ,
, 四组参加数学知识竞答,规则如下:四组之间进行单循环(每组均与另外三组进行一场比赛);每场比赛胜者积3分,负者0分;若出现平局,则比赛双方各积1分.现假设四个组战胜或者负于对手的概率均为
四组参加数学知识竞答,规则如下:四组之间进行单循环(每组均与另外三组进行一场比赛);每场比赛胜者积3分,负者0分;若出现平局,则比赛双方各积1分.现假设四个组战胜或者负于对手的概率均为 ,出现平局的概率为
,出现平局的概率为 ,每场比赛相互独立.
,每场比赛相互独立.
(1)求A组在参加两场比赛后得分为3分的概率;
(2)一轮单循环结束后,求四组总积分一样的情况种数,并计算四组总积分一样的概率.
 ,
, ,
, 四组参加数学知识竞答,规则如下:四组之间进行单循环(每组均与另外三组进行一场比赛);每场比赛胜者积3分,负者0分;若出现平局,则比赛双方各积1分.现假设四个组战胜或者负于对手的概率均为
四组参加数学知识竞答,规则如下:四组之间进行单循环(每组均与另外三组进行一场比赛);每场比赛胜者积3分,负者0分;若出现平局,则比赛双方各积1分.现假设四个组战胜或者负于对手的概率均为 ,出现平局的概率为
,出现平局的概率为 ,每场比赛相互独立.
,每场比赛相互独立.(1)求A组在参加两场比赛后得分为3分的概率;
(2)一轮单循环结束后,求四组总积分一样的情况种数,并计算四组总积分一样的概率.
您最近一年使用:0次
9 . 从某公司生产的产品中任意抽取12件,得到它们的质量(单位: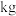 )如下:7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0,则这组数据的四分位数不可能是( )
)如下:7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0,则这组数据的四分位数不可能是( )
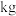 )如下:7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0,则这组数据的四分位数不可能是( )
)如下:7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0,则这组数据的四分位数不可能是( )| A.8.75 | B.8.15 | C.9.9 | D.8.5 |
您最近一年使用:0次
2024-01-26更新
|
833次组卷
|
6卷引用:河南省南阳市第一中学校2023-2024学年高一上学期第四次月考数学试题
河南省南阳市第一中学校2023-2024学年高一上学期第四次月考数学试题 江西省南昌市第二中学2024届高三“九省联考”考后适应性测试数学试题(三)(已下线)黄金卷05(2024新题型)(已下线)热点8-2 概率与统计综合(10题型+满分技巧+限时检测)(已下线)9.2.2?总体百分位数的估计——课后作业(提升版)(已下线)第07讲 第九章 统计 章末重点题型大总结-【帮课堂】(人教A版2019必修第二册)
10 . 甲口袋中装有3个黑球和1个白球,乙口袋中装有3个白球.现同时从甲、乙两口袋中各任取一个球交换放入对方口袋,共进行了2次这样的操作后,甲口袋中恰有2个黑球的概率为
您最近一年使用:0次
2024-01-13更新
|
508次组卷
|
2卷引用:上海市南汇中学2023-2024学年高二上学期期末考试数学试卷



