名校
解题方法
1 . 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入:(4)整体求和等.
例如, ,求证:
,求证: . 证明:原式
. 证明:原式 .
.
波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式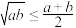 (
( ,
, ),当且仅当
),当且仅当 时等号成立,它是解决最值问题的有力工具.例如:在
时等号成立,它是解决最值问题的有力工具.例如:在 的条件下,当
的条件下,当 为何值时,
为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
解: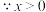 ,
,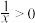 ,
, ,即
,即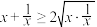 ,
, ,当且仅当
,当且仅当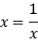 ,即
,即 时,
时, 有最小值,最小值为2.请根据以上阅读材料解答下列问题:
有最小值,最小值为2.请根据以上阅读材料解答下列问题:
(1)已知 ,求
,求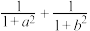 的值.
的值.
(2)若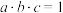 ,解关于
,解关于 的方程
的方程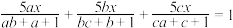 .
.
(3)若正数 ,
, 满足
满足 ,求
,求 的最小值.
的最小值.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入:(4)整体求和等.
例如,
 ,求证:
,求证: . 证明:原式
. 证明:原式 .
.波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式
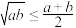 (
( ,
, ),当且仅当
),当且仅当 时等号成立,它是解决最值问题的有力工具.例如:在
时等号成立,它是解决最值问题的有力工具.例如:在 的条件下,当
的条件下,当 为何值时,
为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?解:
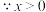 ,
,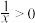 ,
, ,即
,即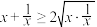 ,
, ,当且仅当
,当且仅当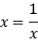 ,即
,即 时,
时, 有最小值,最小值为2.请根据以上阅读材料解答下列问题:
有最小值,最小值为2.请根据以上阅读材料解答下列问题:(1)已知
 ,求
,求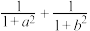 的值.
的值.(2)若
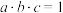 ,解关于
,解关于 的方程
的方程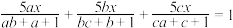 .
.(3)若正数
 ,
, 满足
满足 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2024-07-28更新
|
819次组卷
|
10卷引用:福建省泉州市奕聪中学2024-2025学年高一上学期10月月考数学试卷
福建省泉州市奕聪中学2024-2025学年高一上学期10月月考数学试卷江苏省张家港市沙洲中学2023-2024学年高一上学期第一次月考数学试卷云南省昆明市禄劝彝族苗族自治县民族中学2024-2025学年高一上学期9月月考数学试题江苏省扬州大学附属中学东部分校2024-2025学年高一上学期第一次月考数学试卷广东省珠海市斗门区金砖四校2024-2025学年高一上学期第一次月考(10月)数学试题重庆市万州第三中学2024-2025学年高一上学期第一次月考数学试题山东省枣庄市第二中学2024-2025学年高一上学期10月月考数学试题海南省文昌中学2024-2025学年高一上学期第一次月考数学试题广东省深圳市南山外国语学校(集团)高级中学2024-2025学年高一上学期10月月考数学试卷广东省珠海市第一中学平沙校区2024-2025学年高一上学期10月学业测试数学试题
解题方法
2 . (1)已知 ,设
,设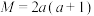 ,
,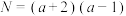 ,比较
,比较 与
与 的大小;
的大小;
(2)证明:已知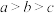 ,且
,且 ,求证:
,求证: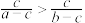 .
.
 ,设
,设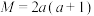 ,
,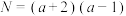 ,比较
,比较 与
与 的大小;
的大小;(2)证明:已知
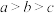 ,且
,且 ,求证:
,求证: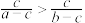 .
.
您最近一年使用:0次
名校
3 . 现定义:设 是非零实常数,若对于任意的
是非零实常数,若对于任意的 ,都有
,都有 ,则称函数
,则称函数 为“关于的
为“关于的 偶型函数”
偶型函数”
(1)请以三角函数为例,写出一个“关于2的偶型函数”的解析式,并给予证明
(2)设定义域为的“关于的 偶型函数”在区间
偶型函数”在区间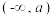 上单调递增,求证在区间
上单调递增,求证在区间 上单调递减
上单调递减
(3)设定义域为 的“关于
的“关于 的偶型函数”
的偶型函数” 是奇函数,若
是奇函数,若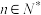 ,请猜测
,请猜测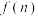 的值,并用数学归纳法证明你的结论
的值,并用数学归纳法证明你的结论
 是非零实常数,若对于任意的
是非零实常数,若对于任意的 ,都有
,都有 ,则称函数
,则称函数 为“关于的
为“关于的 偶型函数”
偶型函数”(1)请以三角函数为例,写出一个“关于2的偶型函数”的解析式,并给予证明
(2)设定义域为的“关于的
 偶型函数”在区间
偶型函数”在区间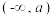 上单调递增,求证在区间
上单调递增,求证在区间 上单调递减
上单调递减(3)设定义域为
 的“关于
的“关于 的偶型函数”
的偶型函数” 是奇函数,若
是奇函数,若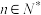 ,请猜测
,请猜测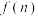 的值,并用数学归纳法证明你的结论
的值,并用数学归纳法证明你的结论
您最近一年使用:0次
2019-12-31更新
|
362次组卷
|
6卷引用:福建省福州第八中学2024-2025学年高一上学期10月月考数学试题
福建省福州第八中学2024-2025学年高一上学期10月月考数学试题上海市静安区2019-2020学年高三上学期期末数学试题2020届上海市静安区高三一模(期末)数学试题(已下线)第四章++数列1(基础过关)-2020-2021学年高二数学单元测试定心卷(人教A版2019选择性必修第二册)(已下线)热点02 函数及其性质-2021年高考数学【热点·重点·难点】专练(上海专用)(已下线)第二章 推理与证明(基础过关)-2020-2021学年高二数学单元测试定心卷(人教版选修2-2)
4 . 已知有限集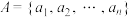 (
( ,
, ),如果
),如果 中的元素
中的元素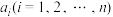 满足
满足 ,就称
,就称 为“完美集”.
为“完美集”.
(1)判断:集合 是否是“完美集”并说明理由;
是否是“完美集”并说明理由;
(2) 、
、 是两个不同的正数,且
是两个不同的正数,且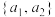 是“完美集”,求证:
是“完美集”,求证: 、
、 至少有一个大于2.
至少有一个大于2.
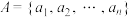 (
( ,
, ),如果
),如果 中的元素
中的元素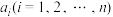 满足
满足 ,就称
,就称 为“完美集”.
为“完美集”.(1)判断:集合
 是否是“完美集”并说明理由;
是否是“完美集”并说明理由;(2)
 、
、 是两个不同的正数,且
是两个不同的正数,且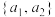 是“完美集”,求证:
是“完美集”,求证: 、
、 至少有一个大于2.
至少有一个大于2.
您最近一年使用:0次
名校
5 . 已知A是非空数集,如果对任意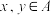 ,都有
,都有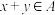 ,
, ,则称A是封闭集.
,则称A是封闭集.
(1)判断集合 ,
,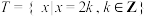 ,是否为封闭集,并说明理由;
,是否为封闭集,并说明理由;
(2)判断命题“若非空集合 ,
, 是封闭集,则
是封闭集,则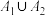 也是封闭集”的真假,并说明理由;
也是封闭集”的真假,并说明理由;
(3)若非空集合A是封闭集合,且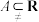 ,求证:
,求证: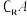 不是封闭集.
不是封闭集.
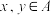 ,都有
,都有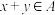 ,
, ,则称A是封闭集.
,则称A是封闭集.(1)判断集合
 ,
,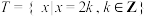 ,是否为封闭集,并说明理由;
,是否为封闭集,并说明理由;(2)判断命题“若非空集合
 ,
, 是封闭集,则
是封闭集,则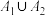 也是封闭集”的真假,并说明理由;
也是封闭集”的真假,并说明理由;(3)若非空集合A是封闭集合,且
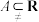 ,求证:
,求证: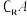 不是封闭集.
不是封闭集.
您最近一年使用:0次
12-13高二·福建福州·阶段练习
名校
6 . 求证:关于x的方程 有一个根为1的充要条件是
有一个根为1的充要条件是 .
.
 有一个根为1的充要条件是
有一个根为1的充要条件是 .
.
您最近一年使用:0次
2024-08-09更新
|
460次组卷
|
40卷引用:福建省厦门市第十中学2023-2024学年高一上学期10月阶段性检测数学试题
福建省厦门市第十中学2023-2024学年高一上学期10月阶段性检测数学试题(已下线)2012-2013学年福建罗源第一中学高二第二次月考理科数学试卷人教B版(2019) 必修第一册 过关斩将 第一章 1.2.3 充分条件、必要条件专题02 充分条件、必要条件、全称量词、存在量词(知识精讲)-【新教材精创】2019-2020高一数学新教材知识讲学(人教A版必修第一册)-《高中新教材知识讲学》(已下线)【新教材精创】1.4+充分条件与必要条件+教学设计(2)-人教A版高中数学必修第一册(已下线)【新教材精创】1.4+充分条件与必要条件+教学设计(1)-人教A版高中数学必修第一册(已下线)【新教材精创】1.4+充分条件与必要条件+学案(1)-人教A版高中数学必修第一册(已下线)【新教材精创】1.4+充分条件与必要条件+学案(2)-人教A版高中数学必修第一册(已下线)1.4充分条件与必要条件-【新教材】人教(A)版高中数学必修第一册限时作业(已下线)1.4 充分、必要条件(精炼)-2020-2021学年一隅三反系列之高一数学新教材必修第一册(人教版A版)【导学案】1.4 充分条件与必要条件-2021-2022学年高一数学《新教材同步精典导学案》(人教A版2019必修第一册)(已下线)2.2 充分条件、必要条件、充要条件海南热带海洋学院附属中学2021-2022学年高一上学期第二次测试数学试题四川省乐山市峨眉文旅综合高中学校2022-2023学年高一上学期第一次月考数学试题陕西省洛南中学2022-2023学年高一上学期期中数学试题人教A版(2019) 必修第一册 数学奇书 学业评价(七) 充要条件北师大版(2019) 必修第一册 数学奇书 第一章 预备知识 §2 常用逻辑用语 §2.1 必要条件与充分条件 第2课时 充要条件(已下线)1.4 充分必要条件(精讲)-《一隅三反》(已下线)1.4.2 充要条件(分层作业)-【上好课】(已下线)第2章 常用逻辑用语 章末题型归纳总结(1)-【帮课堂】(苏教版2019必修第一册)安徽省亳州市蒙城县第八中学2023-2024学年高一上学期9月月考数学试题苏教版(2019)必修第一册课本习题 习题2.2(已下线)高一上学期期中复习【第一章 集合与常用逻辑用语】九大题型归纳(拔尖篇)-举一反三系列(四川省乐山市金口河区延风中学2023-2024学年高一上学期第一次月考数学试题北师大版(2019)必修第一册课本习题第一章复习题江苏省南通市海安高级中学2023-2024学年高一上学期10月阶段检测(一)数学试题(已下线)模块四 专题4 大题分类练 《集合与常用逻辑用语》基础夯实练(已下线)1.4充分条件与必要条件【第二课】(已下线)专题04充分条件与必要条件-【倍速学习法】(人教A版2019必修第一册)(已下线)第二章 常用逻辑用语(压轴题专练)-速记·巧练(苏教版2019必修第一册)(已下线)复习题一(已下线)第04讲 充分条件与必要条件-【暑假预科讲义】(人教A版2019必修第一册)(已下线)第05讲 充分条件、必要条件、充要条件-【暑假自学课】(苏教版2019必修第一册)(已下线)第04讲 充分条件与必要条件-【暑假自学课】(人教A版2019必修第一册)【课后练】 1.2.2 充分条件和必要条件 课后作业-湘教版(2019)必修(第一册)第1章 集合与逻辑山西省实验中学2024-2025学年高一上学期第一次月考数学试卷安徽省亳州市涡阳县2024-2025学年高一上学期10月月考数学试题山东省泰安市泰山国际学校2024—2025学年高一上学期10月月考数学试题山西省大同市浑源县第七中学校2024-2025学年高一上学期第二次月考数学试题陕西省咸阳市实验中学2020-2021学年高二上学期第三次月考数学(文)试题
名校
7 . 已知正实数集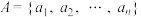 ,定义:
,定义: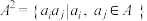 称为
称为 的平方集.记
的平方集.记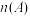 为集合
为集合 中的元素个数.
中的元素个数.
(1)若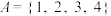 ,
,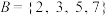 求集合
求集合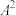 和
和 ;
;
(2)若 ,求
,求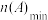 ;
;
(3)①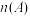 分别取1,2,3时,试比较
分别取1,2,3时,试比较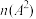 和
和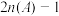 的大小关系;
的大小关系;
②猜想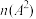 和
和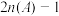 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
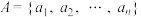 ,定义:
,定义: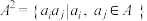 称为
称为 的平方集.记
的平方集.记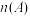 为集合
为集合 中的元素个数.
中的元素个数.(1)若
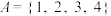 ,
,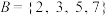 求集合
求集合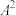 和
和 ;
;(2)若
 ,求
,求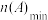 ;
;(3)①
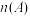 分别取1,2,3时,试比较
分别取1,2,3时,试比较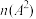 和
和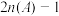 的大小关系;
的大小关系;②猜想
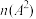 和
和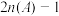 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
您最近一年使用:0次
7日内更新
|
159次组卷
|
2卷引用:福建省同安第一中学2024-2025学年高一上学期第一次月考数学试卷
名校
解题方法
8 . 已知函数 的定义域为
的定义域为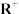 ,对任意的
,对任意的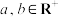 ,都有
,都有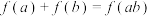 .当
.当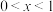 时,
时, .
.
(1)求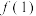 的值,并证明:当
的值,并证明:当 时,
时, ;
;
(2)判断 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(3)若 ,求不等式
,求不等式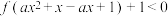 的解集.
的解集.
 的定义域为
的定义域为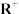 ,对任意的
,对任意的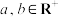 ,都有
,都有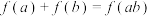 .当
.当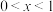 时,
时, .
.(1)求
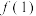 的值,并证明:当
的值,并证明:当 时,
时, ;
;(2)判断
 的单调性,并证明你的结论;
的单调性,并证明你的结论;(3)若
 ,求不等式
,求不等式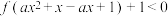 的解集.
的解集.
您最近一年使用:0次
2024-11-01更新
|
1869次组卷
|
3卷引用:福建省龙岩市第二中学2024-2025学年高一上学期第一次月考数学试题
名校
解题方法
9 . 若一个集合含有 个元素
个元素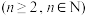 ,且这
,且这 个元素之和等于这
个元素之和等于这 个元素之积,则称该集合为
个元素之积,则称该集合为 元“复活集”.
元“复活集”.
(1)直接写出一个2元“复活集”(无需写出求解过程);
(2)求证:对任意一个2元“复活集”,若其元素均为正数,则其元素之积一定大于4;
(3)是否存在某个3元“复活集”,其元素均为正整数?若存在,求出所有符合条件的3元“复活集”;若不存在,说明理由.
 个元素
个元素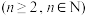 ,且这
,且这 个元素之和等于这
个元素之和等于这 个元素之积,则称该集合为
个元素之积,则称该集合为 元“复活集”.
元“复活集”.(1)直接写出一个2元“复活集”(无需写出求解过程);
(2)求证:对任意一个2元“复活集”,若其元素均为正数,则其元素之积一定大于4;
(3)是否存在某个3元“复活集”,其元素均为正整数?若存在,求出所有符合条件的3元“复活集”;若不存在,说明理由.
您最近一年使用:0次
7日内更新
|
116次组卷
|
2卷引用:福建省福州高级中学2024-2025学年高一上学期10月月考数学试卷
名校
10 . 已知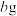 糖水中有
糖水中有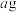 糖(
糖(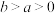 ),往糖水中加入
),往糖水中加入 糖(
糖( ),(假设全部溶解)糖水更甜了.
),(假设全部溶解)糖水更甜了.
(1)请将这个事实表示为一个不等式,证明这个不等式;
(2)利用(1)的结论比较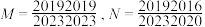 的大小;
的大小;
(3)证明命题:设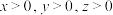 ,证明:
,证明: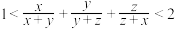 .
.
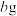 糖水中有
糖水中有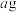 糖(
糖(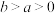 ),往糖水中加入
),往糖水中加入 糖(
糖( ),(假设全部溶解)糖水更甜了.
),(假设全部溶解)糖水更甜了.(1)请将这个事实表示为一个不等式,证明这个不等式;
(2)利用(1)的结论比较
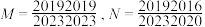 的大小;
的大小;(3)证明命题:设
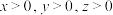 ,证明:
,证明: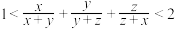 .
.
您最近一年使用:0次
2024-10-19更新
|
190次组卷
|
2卷引用:福建省安溪铭选中学2024-2025学年高一上学期第一次月考数学试卷



