1 . 已知实数 ,
, ,
, ,
, 满足:
满足: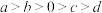 ,则下列不等式一定正确的是( )
,则下列不等式一定正确的是( )
 ,
, ,
, ,
, 满足:
满足: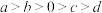 ,则下列不等式一定正确的是( )
,则下列不等式一定正确的是( )A. | B. | C. | D. |
您最近半年使用:0次
解题方法
2 . 对于实数 ,下列命题中正确的是( )
,下列命题中正确的是( )
 ,下列命题中正确的是( )
,下列命题中正确的是( )A.若 ,则 ,则 | B.若 ,则 ,则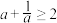 |
C.若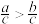 ,则 ,则 | D.若 , , ,则 ,则 |
您最近半年使用:0次
2024·全国·模拟预测
解题方法
3 . 已知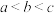 ,且
,且 ,则下列结论成立的是( )
,则下列结论成立的是( )
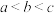 ,且
,且 ,则下列结论成立的是( )
,则下列结论成立的是( )A.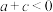 | B. |
C.存在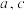 使得 使得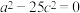 | D.若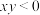 且 且 ,则 ,则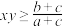 |
您最近半年使用:0次
4 . 下列说法正确的是( )
A.若 ,则 ,则 | B.若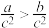 ,则 ,则 |
C.若 , , ,则 ,则 | D.若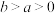 ,则 ,则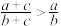 |
您最近半年使用:0次
解题方法
5 . 已知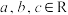 ,则下列命题为假命题的是( )
,则下列命题为假命题的是( )
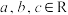 ,则下列命题为假命题的是( )
,则下列命题为假命题的是( )A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则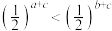 | D.若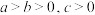 ,则 ,则 |
您最近半年使用:0次
6 . 设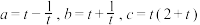 ,其中
,其中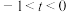 ,则( )
,则( )
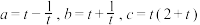 ,其中
,其中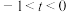 ,则( )
,则( )A.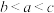 | B. |
C.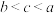 | D.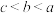 |
您最近半年使用:0次
解题方法
7 . 已知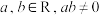 ,且
,且 ,则( )
,则( )
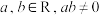 ,且
,且 ,则( )
,则( )A.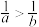 | B.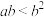 | C. | D. |
您最近半年使用:0次
8 . 目前发射人造天体,多采用多级火箭作为运载工具.其做法是在前一级火箭燃料燃烧完后,连同其壳体一起抛掉,让后一级火箭开始工作,使火箭系统加速到一定的速度时将人造天体送入预定轨道.现有材料科技条件下,对于一个 级火箭,在第
级火箭,在第 级火箭的燃料耗尽时,火箭的速度可以近似表示为
级火箭的燃料耗尽时,火箭的速度可以近似表示为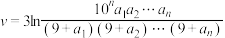 ,
,
其中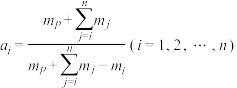 .
.
注: 表示人造天体质量,
表示人造天体质量, 表示第
表示第 (
(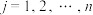 )级火箭结构和燃料的总质量.
)级火箭结构和燃料的总质量.
给出下列三个结论:
① ;
;
②当 时,
时,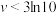 ;
;
③当 时,若
时,若 ,则
,则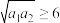 .
.
其中所有正确结论的序号是___________ .
 级火箭,在第
级火箭,在第 级火箭的燃料耗尽时,火箭的速度可以近似表示为
级火箭的燃料耗尽时,火箭的速度可以近似表示为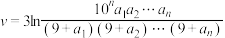 ,
,其中
 .
.注:
 表示人造天体质量,
表示人造天体质量, 表示第
表示第 (
(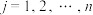 )级火箭结构和燃料的总质量.
)级火箭结构和燃料的总质量.给出下列三个结论:
①
 ;
;②当
 时,
时,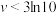 ;
;③当
 时,若
时,若 ,则
,则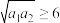 .
.其中所有正确结论的序号是
您最近半年使用:0次
9 . 下列命题中真命题是( )
A.若 ,则 ,则 | B.若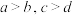 ,则 ,则 |
C.若 ,则 ,则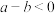 | D.若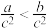 ,则 ,则 |
您最近半年使用:0次
名校
解题方法
10 . 我国著名科幻作家刘慈欣的小说《三体Ⅱ·黑暗森林》中的“水滴”是三体文明使用新型材料-强互作用力(SIM)材料所制成的宇宙探测器,其外形与水滴相似,某科研小组研发的新材料水滴角测试结果如图所示(水滴角可看作液、固、气三相交点处气—液两相界面的切线与液—固两相交线所成的角),圆法和椭圆法是测量水滴角的常用方法,即将水滴轴截面看成圆或者椭圆(长轴平行于液—固两者的相交线,椭圆的短半轴长小于圆的半径)的一部分,设图中用圆法和椭圆法测量所得水滴角分别为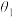 ,
,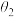 ,则( )
,则( )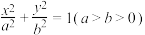 上一点
上一点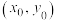 处的切线方程为
处的切线方程为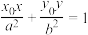 .
.
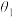 ,
,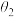 ,则( )
,则( )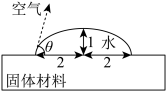
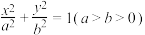 上一点
上一点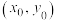 处的切线方程为
处的切线方程为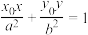 .
.A. | B. |
C.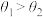 | D.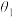 和 和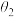 的大小关系无法确定 的大小关系无法确定 |
您最近半年使用:0次
7日内更新
|
277次组卷
|
5卷引用:2024届高三星云二月线上调研考试数学试题
2024届高三星云二月线上调研考试数学试题(已下线)最新模拟重组精华卷1-模块一 各地期末考试精选汇编江西省八所重点中学2024届高三下学期4月联考数学试卷江西省八所重点中学2024届高三下学期4月联考数学试卷(已下线)压轴小题11 圆与抛物线交点的切线问题(压轴小题)



