名校
1 . 已知 ,函数
,函数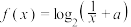 .
.
(1)当 时,解不等式
时,解不等式 ;
;
(2)若关于 的方程
的方程 有且仅有一解,求
有且仅有一解,求 的取值范围.
的取值范围.
 ,函数
,函数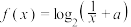 .
.(1)当
 时,解不等式
时,解不等式 ;
;(2)若关于
 的方程
的方程 有且仅有一解,求
有且仅有一解,求 的取值范围.
的取值范围.
您最近一年使用:0次
2019-11-06更新
|
244次组卷
|
2卷引用:上海市金山中学2016-2017学年高二上学期8月摸底数学试题
19-20高一·浙江·阶段练习
2 . 化简、求值:
(1)化简: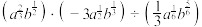 ;
;
(2)已知 ,求实数
,求实数 的值;
的值;
(3)计算: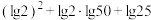 .
.
(1)化简:
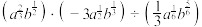 ;
;(2)已知
 ,求实数
,求实数 的值;
的值;(3)计算:
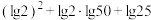 .
.
您最近一年使用:0次
名校
3 . 若函数 在
在 上为增函数,则方程组
上为增函数,则方程组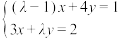 解的组数为
解的组数为____ .
 在
在 上为增函数,则方程组
上为增函数,则方程组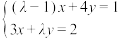 解的组数为
解的组数为
您最近一年使用:0次
2019-12-03更新
|
130次组卷
|
2卷引用:上海市十四校(原十三校)2016-2017学年高三上学期12月联考数学试题
12-13高一上·浙江杭州·阶段练习
解题方法
4 . (I)计算: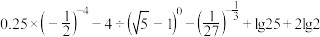 ;
;
(II)已知定义在区间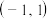 上的奇函数
上的奇函数 单调递增.解关于
单调递增.解关于 的不等式
的不等式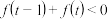
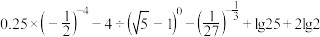 ;
;(II)已知定义在区间
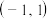 上的奇函数
上的奇函数 单调递增.解关于
单调递增.解关于 的不等式
的不等式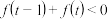
您最近一年使用:0次
名校
5 . 已知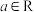 ,函数
,函数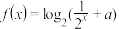 .
.
(Ⅰ)当 时,解不等式
时,解不等式 ;
;
(Ⅱ)若关于 的方程
的方程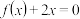 的解集中恰有一个元素,求
的解集中恰有一个元素,求 的取值范围;
的取值范围;
(Ⅲ)设 ,若对任意
,若对任意 ,函数
,函数 在区间
在区间 上的最大值与最小值的和不大于
上的最大值与最小值的和不大于 ,求
,求 的取值范围.
的取值范围.
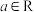 ,函数
,函数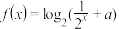 .
.(Ⅰ)当
 时,解不等式
时,解不等式 ;
;(Ⅱ)若关于
 的方程
的方程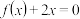 的解集中恰有一个元素,求
的解集中恰有一个元素,求 的取值范围;
的取值范围;(Ⅲ)设
 ,若对任意
,若对任意 ,函数
,函数 在区间
在区间 上的最大值与最小值的和不大于
上的最大值与最小值的和不大于 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2018-01-26更新
|
1931次组卷
|
2卷引用:天津市新四区示范校2017-2018学年高一上学期期末联考数学试题
6 . 方程组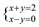 的解构成的集合是
的解构成的集合是
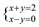 的解构成的集合是
的解构成的集合是 A. | B.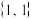 | C.(1,1) | D.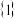 |
您最近一年使用:0次
名校
解题方法
7 . 一般地,我们把函数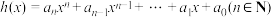 称为多项式函数,其中系数
称为多项式函数,其中系数 ,
, ,…,
,…,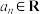 .设
.设 ,
, 为两个多项式函数,且对所有的实数
为两个多项式函数,且对所有的实数 等式
等式 恒成立.
恒成立.
(1)若 ,
,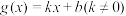 .
.
①求 的表达式;
的表达式;
②解不等式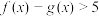 .
.
(2)若方程 无实数根,证明方程
无实数根,证明方程 也无实数解.
也无实数解.
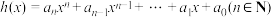 称为多项式函数,其中系数
称为多项式函数,其中系数 ,
, ,…,
,…,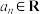 .设
.设 ,
, 为两个多项式函数,且对所有的实数
为两个多项式函数,且对所有的实数 等式
等式 恒成立.
恒成立.(1)若
 ,
,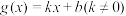 .
.①求
 的表达式;
的表达式;②解不等式
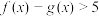 .
.(2)若方程
 无实数根,证明方程
无实数根,证明方程 也无实数解.
也无实数解.
您最近一年使用:0次
2017-10-31更新
|
454次组卷
|
3卷引用:北京西城35中2016-2017学年高一上学期期中数学试题
13-14高一上·广东·期中
8 . 化简、求值:
(1)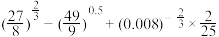 ;
;
(2)计算
(1)
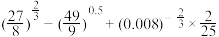 ;
; (2)计算

您最近一年使用:0次
2016-12-02更新
|
1034次组卷
|
4卷引用:2017届山西省名校高三9月联考数学(文)试卷2
2017届山西省名校高三9月联考数学(文)试卷2(已下线)2013-2014学年广东省实验中学高一上学期期中模块考试数学试卷2014-2015学年四川省峨眉山市第二中学高一上学期期中考试数学试卷2015-2016学年安徽省蚌埠市二中高一上学期期中数学试卷
名校
解题方法
9 . 已知函数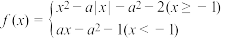 (
( ).
).
(1)当 时,解不等式
时,解不等式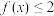 ;
;
(2)证明:方程 最少有1个解,最多有2个解,并求该方程有2个解时实数
最少有1个解,最多有2个解,并求该方程有2个解时实数 的取值范围.
的取值范围.
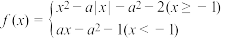 (
( ).
).(1)当
 时,解不等式
时,解不等式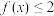 ;
;(2)证明:方程
 最少有1个解,最多有2个解,并求该方程有2个解时实数
最少有1个解,最多有2个解,并求该方程有2个解时实数 的取值范围.
的取值范围.
您最近一年使用:0次
2017-08-15更新
|
631次组卷
|
2卷引用:浙江省东阳中学2017-2018学年高一6月月考数学试题

 的解构成的集合是
的解构成的集合是