1 . 我国南北朝的伟大科学教祖暅于5世纪提出了著名的祖暅原理,意思就是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个几截面的面积总相等,那么这两个几何体的体积相等.如图1,为了求半球的体积,可以构造一个底面半径和高都与半球的半径相等的圆柱,与半球放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一个新几何体,用任何一个平行底面的平面去截它们时,两个截面面积总相等.如图2,某个清代陶瓷容器的上、下底面为互相平行的圆面(上底面开口,下底面封闭),侧面为球面的一部分,上、下底面圆半径都为6cm,且它们的距离为24cm,则该容器的容积为______  (容器的厚度忽略不计).
(容器的厚度忽略不计).
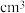 (容器的厚度忽略不计).
(容器的厚度忽略不计).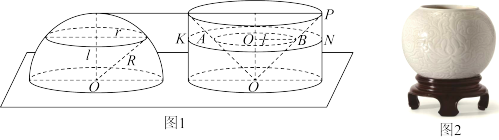
您最近一年使用:0次
名校
解题方法
2 . 风筝又称为“纸鸢”,由中国古代劳动人民发明于距今2000多年的东周春秋时期,相传墨翟以木头制成木鸟,研制三年而成,是人类最早的风筝起源.如图,是某高一年级学生制作的一个风筝模型的多面体ABCEF,D为AB的中点,四边形EFDC为矩形,且 ,
,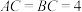 ,
,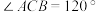 ,当
,当 时,多面体ABCEF的体积为( )
时,多面体ABCEF的体积为( )
 ,
,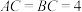 ,
,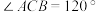 ,当
,当 时,多面体ABCEF的体积为( )
时,多面体ABCEF的体积为( )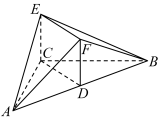
A.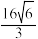 | B.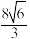 | C. | D. |
您最近一年使用:0次
解题方法
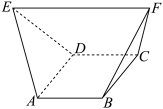
3 . 木楔在传统木工中运用广泛.如图,某木楔可视为一个五面体,其中四边形 是边长为2的正方形,且
是边长为2的正方形,且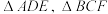 均为等边三角形,
均为等边三角形, ,
,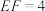 ,则该木楔的体积为( )
,则该木楔的体积为( )
 是边长为2的正方形,且
是边长为2的正方形,且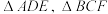 均为等边三角形,
均为等边三角形, ,
,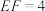 ,则该木楔的体积为( )
,则该木楔的体积为( )
A. | B. | C.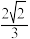 | D.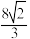 |
您最近一年使用:0次
4 . 刍甍(chú méng)是中国古代数学书中提到的一种几何体,《九章算术》中对其有记载:“下有袤有广,而上有袤无广.”可翻译为:“底面有长有宽为矩形,顶部只有长没有宽为一条棱.”如图,在刍甍 中,四边形
中,四边形 是边长为2的正方形,
是边长为2的正方形,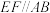 ,
, 到平面
到平面 的距离为3,则该刍甍的体积可能是( )
的距离为3,则该刍甍的体积可能是( )
 中,四边形
中,四边形 是边长为2的正方形,
是边长为2的正方形,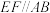 ,
, 到平面
到平面 的距离为3,则该刍甍的体积可能是( )
的距离为3,则该刍甍的体积可能是( )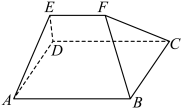
A. | B.4 | C.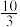 | D.3 |
您最近一年使用:0次
2023-07-14更新
|
320次组卷
|
3卷引用:黄金卷08
5 . 坡屋顶是我国传统建筑造型之一,蕴含着丰富的数学元素.安装灯带可以勾勒出建筑轮廓,展现造型之美.如图,某坡屋顶可视为一个五面体,其中两个面是全等的等腰梯形,两个面是全等的等腰三角形.若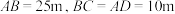 ,且等腰梯形所在的平面、等腰三角形所在的平面与平面
,且等腰梯形所在的平面、等腰三角形所在的平面与平面 的夹角的正切值均为
的夹角的正切值均为 ,则该五面体的所有棱长之和为( )
,则该五面体的所有棱长之和为( )
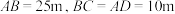 ,且等腰梯形所在的平面、等腰三角形所在的平面与平面
,且等腰梯形所在的平面、等腰三角形所在的平面与平面 的夹角的正切值均为
的夹角的正切值均为 ,则该五面体的所有棱长之和为( )
,则该五面体的所有棱长之和为( )
A. | B. |
C. | D.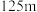 |
您最近一年使用:0次
2023-06-19更新
|
11473次组卷
|
26卷引用:2023年北京高考数学真题
2023年北京高考数学真题(已下线)北京十年真题专题07立体几何与空间向量北京十年真题专题07立体几何与空间向量北京市第一零一中学2023-2024学年高三上学期数学统练五北京市东城区第五十五中学2024届高三上学期12月月考数学试题北京市第八十中学2023-2024学年高三上学期10月月考数学试卷专题09立体几何与空间向量(第二部分)(已下线)五年北京专题06立体几何与空间向量(已下线)三年北京专题06立体几何与空间向量专题06空间向量与立体几何(成品)(已下线)2023年北京高考数学真题变式题6-10(已下线)考点9 垂直的判定与性质 2024届高考数学考点总动员北京市东城区第一六六中学2023-2024学年高二上学期期末模拟数学试题(已下线)技巧03 数学文化与数学阅读解题技巧(4大核心考点)(讲义)天津市第一中学滨海学校2024届高三第六次学业水平质量调查数学试卷(开学考)(已下线)专题7.2 空间中的位置关系【十大题型】(已下线)专题7.3 空间角与空间中的距离问题【九大题型】(已下线)第二章 立体几何中的计算 专题一 空间角 微点6 二面角大小的计算(一)【基础版】(已下线)重难点11 立体几何常考经典小题全归类【九大题型】(已下线)专题14 立体几何选择题(理科)-1(已下线)专题13 立体几何选择题(文科)-1专题07立体几何与空间向量(已下线)第04讲 利用几何法解决空间角和距离19种常见考法归类(5)湖北省武汉市部分重点中学2023-2024学年高二上学期9月阶段性检测数学试题(已下线)【一题多变】图形辨析 立足特征(已下线)8.6.3平面与平面垂直【第三课】“上好三节课,做好三套题“高中数学素养晋级之路
名校
解题方法
6 . “牟合方盖”是我国古代数学家刘徽在研究球的体积过程中构造的一个和谐优美的几何模型.如图1,正方体的棱长为2,用一个底面直径为2的圆柱面去截该正方体,沿着正方体的前后方向和左右方向各截一次,截得的公共部分即是一个牟合方盖(如图2).已知这个牟合方盖与正方体外接球的体积之比为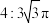 ,则正方体除去牟合方盖后剩余部分的体积为( )
,则正方体除去牟合方盖后剩余部分的体积为( )
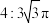 ,则正方体除去牟合方盖后剩余部分的体积为( )
,则正方体除去牟合方盖后剩余部分的体积为( )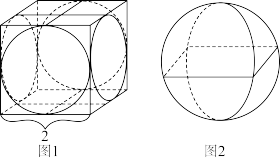
A. | B.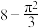 |
C. | D.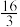 |
您最近一年使用:0次
2023-05-25更新
|
689次组卷
|
3卷引用:北京市2023届高三高考模拟预测考试数学试题
名校
解题方法
7 . 数学中有许多形状优美,寓意独特的几何体,“勒洛四面体”就是其中之一.勒洛四面体是以正四面体的四个顶点为球心,以正四面体的棱长为半径的四个球的公共部分.如图,在勒洛四面体中,正四面体 的棱长为
的棱长为 ,则下列结论正确的是( )
,则下列结论正确的是( )
 的棱长为
的棱长为 ,则下列结论正确的是( )
,则下列结论正确的是( )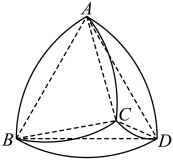
| A.勒洛四面体最大的截面是正三角形 |
B.若 、 、 是勒洛四面体 是勒洛四面体 表面上的任意两点,则 表面上的任意两点,则 的最大值为 的最大值为 |
C.勒洛四面体 的体积是 的体积是 |
D.勒洛四面体 内切球的半径是 内切球的半径是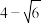 |
您最近一年使用:0次
2023-04-10更新
|
1748次组卷
|
6卷引用:数学(北京卷)
(已下线)数学(北京卷)北京市海淀区北京交大附中2024届高三上学期12月诊断练习数学试题天津教研联盟2023届高三一模数学试题河北省保定市唐县第二中学2024届高三上学期12月月考数学试题(已下线)第二章 立体几何中的计算 专题三 空间体积的计算 微点7 空间图形体积的计算综合训练【培优版】广东省深圳市盐田区深圳外国语学校2022-2023学年高二下学期5月月考数学试题
8 . 如图是一个底面半径和高都是1的装满沙子的圆锥形沙漏,从计时开始,流出沙子的体积 是沙面下降高度
是沙面下降高度 的函数
的函数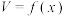 ,若正数
,若正数 ,
, 满足
满足 ,则
,则 的最大值为( )
的最大值为( )
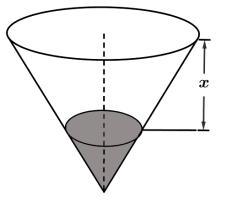
 是沙面下降高度
是沙面下降高度 的函数
的函数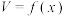 ,若正数
,若正数 ,
, 满足
满足 ,则
,则 的最大值为( )
的最大值为( )
A. | B.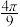 | C.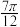 | D.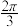 |
您最近一年使用:0次
2021-05-05更新
|
574次组卷
|
5卷引用:北京市十一学校2022届高三4月月考数学试题
北京市十一学校2022届高三4月月考数学试题陕西省宝鸡市2021届高三下学期二模理科数学试题全国Ⅱ卷决胜高考2021届高三数学(理)仿真卷试题(六)(已下线)专题4.4 立体几何中最值问题-玩转压轴题,进军满分之2021高考数学选择题填空题苏教版(2019) 必修第二册 过关斩将 第13章 本章复习提升
名校
解题方法
9 . 《九章算术》中,称四个面均为直角三角形的四面体为“鳖臑”.已知某“鳖臑”的三视图如图所示,则该“鳖臑”的体积_____________ .
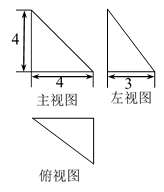
您最近一年使用:0次
2021-05-05更新
|
534次组卷
|
4卷引用:北京市中央民族大学附属中学2021届高三三模数学试题
北京市中央民族大学附属中学2021届高三三模数学试题上海市嘉定区2021届高三二模数学试题(已下线)课时44 几何体的表面积与体积-2022年高考数学一轮复习小题多维练(上海专用)四川省成都市成华区某校2023-2024学年高三“三诊”数学(文)试题
10 . 瑞士著名数学家欧拉在1765年证明了定理:三角形的外心、重心、垂心位于同一条直线上,这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中作 ,
,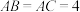 ,点
,点 ,点
,点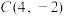 ,且其“欧拉线”与圆
,且其“欧拉线”与圆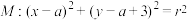 相切.则圆
相切.则圆 上的点到直线
上的点到直线 的距离的最小值为( )
的距离的最小值为( )
 ,
,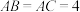 ,点
,点 ,点
,点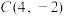 ,且其“欧拉线”与圆
,且其“欧拉线”与圆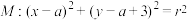 相切.则圆
相切.则圆 上的点到直线
上的点到直线 的距离的最小值为( )
的距离的最小值为( )A. | B. | C. | D.6 |
您最近一年使用:0次



