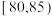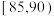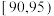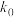1 . 2020年,由于新冠肺炎疫情的影响,2月底学生不能如期到学校上课,某校决定采用教育网络平台和老师钉钉教学相结合的方式进行授课,并制定了相应的网络学习规章制度,学生居家学习经过一段时间授课,学校教务处对高一学生能否严格遵守学校安排,完成居家学习的情况进行调查,现从高一年级随机抽取了 两个班级,并得到如表数据:
两个班级,并得到如表数据:
(1)补全下面的 列联表,并且根据调查的数据,判断能否在犯错误的概率不超过0.005的前提下认为“学生能严格遵守学校安排,完成居家学习”和学生所在班级有关系;
列联表,并且根据调查的数据,判断能否在犯错误的概率不超过0.005的前提下认为“学生能严格遵守学校安排,完成居家学习”和学生所在班级有关系;
(2)网络授课结束后,高一年级800名学生进行了测试,学生的数学成绩近似服从正态分布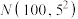 ,若90分以下都算不及格,问高一年级不及格的学生有多少人?
,若90分以下都算不及格,问高一年级不及格的学生有多少人?
附1:参考公式: ;
;
附2:若随机变量X服从正态分布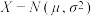 ,则
,则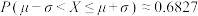 ,
,
 两个班级,并得到如表数据:
两个班级,并得到如表数据:| A班 | B班 | 合计 | |
| 严格遵守 | 36 | 56 | |
| 不能严格遵守 | |||
| 合计 | 50 | 50 |
 列联表,并且根据调查的数据,判断能否在犯错误的概率不超过0.005的前提下认为“学生能严格遵守学校安排,完成居家学习”和学生所在班级有关系;
列联表,并且根据调查的数据,判断能否在犯错误的概率不超过0.005的前提下认为“学生能严格遵守学校安排,完成居家学习”和学生所在班级有关系;(2)网络授课结束后,高一年级800名学生进行了测试,学生的数学成绩近似服从正态分布
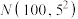 ,若90分以下都算不及格,问高一年级不及格的学生有多少人?
,若90分以下都算不及格,问高一年级不及格的学生有多少人?附1:参考公式:
 ;
;附2:若随机变量X服从正态分布
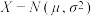 ,则
,则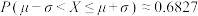 ,
,
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
您最近一年使用:0次
名校
解题方法
2 . 某研究型学习小组调查研究“中学生使用智能手机对学习的影响”,对我校80名学生调查得到部分统计数据如下表,记 为事件:“学习成绩优秀且不使用手机”;
为事件:“学习成绩优秀且不使用手机”; 为事件:“学习成绩不优秀且不使用手机”,且已知事件
为事件:“学习成绩不优秀且不使用手机”,且已知事件 的频率是事件
的频率是事件 的频率的2倍.
的频率的2倍.
(1)求表中 的值,并补全表中所缺数据;
的值,并补全表中所缺数据;
(2)运用独立性检验思想,判断是否有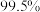 的把握认为中学生使用手机对学习有影响?
的把握认为中学生使用手机对学习有影响?
参考数据: ,其中
,其中 .
.
 为事件:“学习成绩优秀且不使用手机”;
为事件:“学习成绩优秀且不使用手机”; 为事件:“学习成绩不优秀且不使用手机”,且已知事件
为事件:“学习成绩不优秀且不使用手机”,且已知事件 的频率是事件
的频率是事件 的频率的2倍.
的频率的2倍.不使用手机 | 使用手机 | 合计 | |
学习成绩优秀人数 |
| 12 | |
学习成绩不优秀人数 |
| 26 | |
合计 |
 的值,并补全表中所缺数据;
的值,并补全表中所缺数据;(2)运用独立性检验思想,判断是否有
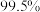 的把握认为中学生使用手机对学习有影响?
的把握认为中学生使用手机对学习有影响?参考数据:
 ,其中
,其中 .
. |  |  |  |  |  |
 |  |  |  |  |  |
您最近一年使用:0次
解题方法
3 . 北京冬季奥运会于2022年2月4日至2022年2月20日在中华人民共和国北京市和河北省张家口市联合举行.这是中国历史上第一次举办冬季奥运会,北京、张家口同为主办城市,也是中国继北京奥运会、南京青奥会之后第三次举办奥运赛事.北京冬奥组委对报名参加北京冬奥会志愿者的人员开展冬奥会志愿者的培训活动,并在培训结束后进行了一次考核.为了解这次培训活动的效果,从中随机抽取160名志愿者的考核成绩,根据这160名志愿者的考核成绩,得到的统计图表如下所示.
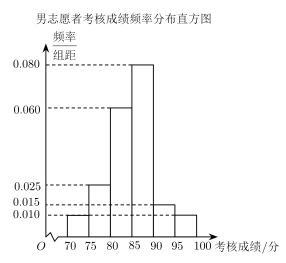
若参加这次考核的志愿者考核成绩在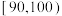 内,则考核等级为优秀.
内,则考核等级为优秀.
(1)求a,b,m的值;
(2)分别求出这次培训考核等级为优秀的男、女志愿者人数;
(3)补全下面的2×2列联表,在犯错概率不超过0.01的条件下,能否认为考核等级是否优秀与性别有关.
参考公式: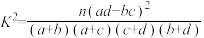 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
女志愿者考核成绩频率分布表
分组 | 频数 | 频率 |
| 4 | 0.050 |
| 26 | 0.325 |
| a | 0.3 |
| 20 | m |
| b | 0.075 |

若参加这次考核的志愿者考核成绩在
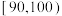 内,则考核等级为优秀.
内,则考核等级为优秀.(1)求a,b,m的值;
(2)分别求出这次培训考核等级为优秀的男、女志愿者人数;
(3)补全下面的2×2列联表,在犯错概率不超过0.01的条件下,能否认为考核等级是否优秀与性别有关.
优秀 | 非优秀 | 合计 | |
男志愿者 | |||
女志愿者 | |||
合计 |
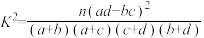 ,其中n=a+b+c+d.
,其中n=a+b+c+d.参考数据:
| 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
您最近一年使用:0次
2022-05-27更新
|
482次组卷
|
3卷引用:东北三省四市教研联合体2022届高三下学期模拟试卷(二)文科数学试题
名校
解题方法
4 . 随着手机的日益普及,学生使用手机对学校管理和学生发展带来诸多不利影响.为保护学生视力,让学生在学校专心学习,防止沉迷网络和游戏,促进学生身心健康发展,教育部于2021年1月15日下发文件《关于加强中小学生手机管理工作的通知》,对中小学生的手机使用和管理作出了相关的规定某研究型学习小组调查研究“中学生使用智能手机对学习的影响”,对我校80名学生调查得到部分统计数据如下表,记 为事件:“学习成绩优秀且不使用手机”;
为事件:“学习成绩优秀且不使用手机”; 为事件:“学习成绩不优秀且不使用手机”,且已知事件
为事件:“学习成绩不优秀且不使用手机”,且已知事件 的频率是事件
的频率是事件 的频率的2倍.
的频率的2倍.
(1)求表中 ,
, 的值,并补全表中所缺数据;
的值,并补全表中所缺数据;
(2)运用独立性检验思想,判断是否有99.9%的把握认为中学生使用手机对学习有影响?
参考数据: ,其中
,其中 .
.
 为事件:“学习成绩优秀且不使用手机”;
为事件:“学习成绩优秀且不使用手机”; 为事件:“学习成绩不优秀且不使用手机”,且已知事件
为事件:“学习成绩不优秀且不使用手机”,且已知事件 的频率是事件
的频率是事件 的频率的2倍.
的频率的2倍.不使用手机 | 使用手机 | 合计 | |
学习成绩优秀人数 |
| 10 | |
学习成绩不优秀人数 |
| 25 | |
合计 |
(1)求表中
 ,
, 的值,并补全表中所缺数据;
的值,并补全表中所缺数据;(2)运用独立性检验思想,判断是否有99.9%的把握认为中学生使用手机对学习有影响?
参考数据:
 ,其中
,其中 .
. | 0.10 | 0.05 | 0.01 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
解题方法
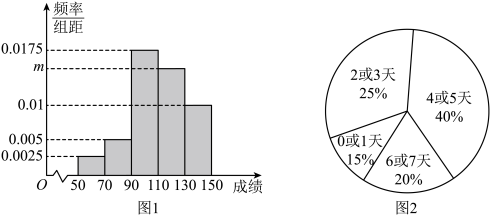
5 . 为了研究学生每天整理数学错题的情况,某课题组在某市中学生中随机抽取了100名学生调查了他们期中考试的数学成绩和平时整理数学错题情况,并绘制了下列两个统计图表,图1为学生期中考试数学成绩的频率分布直方图,图2为学生一个星期内整理数学错题天数的扇形图.若本次数学成绩在110分及以上视为优秀,将一个星期有4天及以上整理数学错题视为“经常整理”,少于4天视为“不经常整理”. 已知数学成绩优秀的学生中,经常整理错题的学生占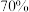 .
.
(1)求图1中 的值;
的值;
(2)根据图1、图2中的数据,补全上方 列联表,并根据小概率值
列联表,并根据小概率值 的独立性检验,分析数学成绩优秀与经常整理数学错题是否有关?
的独立性检验,分析数学成绩优秀与经常整理数学错题是否有关?
(3)用频率估计概率,在全市中学生中按“经常整理错题”与“不经常整理错题”进行分层抽样,随机抽取5名学生,再从这5名学生中随机抽取2人进行座谈.求这2名同学中经常整理错题且数学成绩优秀的人数恰为1人的概率.
附: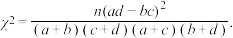
 .
.
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
经常整理 | |||
不经常整理 | |||
合计 |
 的值;
的值;(2)根据图1、图2中的数据,补全上方
 列联表,并根据小概率值
列联表,并根据小概率值 的独立性检验,分析数学成绩优秀与经常整理数学错题是否有关?
的独立性检验,分析数学成绩优秀与经常整理数学错题是否有关?(3)用频率估计概率,在全市中学生中按“经常整理错题”与“不经常整理错题”进行分层抽样,随机抽取5名学生,再从这5名学生中随机抽取2人进行座谈.求这2名同学中经常整理错题且数学成绩优秀的人数恰为1人的概率.
附:
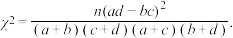
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
您最近一年使用:0次
2023-05-31更新
|
767次组卷
|
5卷引用:吉林省长春博硕学校2022-2023学年高二下学期期中考试数学试题
2022·全国·模拟预测
解题方法
6 . 第24届冬季奥林匹克运动会于2022年2月4日开幕,观众可以通过中央电视台综合频道观看比赛实况.某机构对某社区群众每天观看比赛的情况进行调查,将每天观看比赛时间超过3小时的人称为“冬奥迷”,否则称为“非冬奥迷”,从调查结果中随机抽取50份进行分析,得到数据如表所示:
(1)补全 列联表,并判断是否有99%的把握认为是否为“冬奥迷”与性别有关?
列联表,并判断是否有99%的把握认为是否为“冬奥迷”与性别有关?
(2)现从抽取的“冬奥迷”人群中,按性别采用分层抽样的方法抽取6人,然后从这6人中随机抽取2人,记这2人中男“冬奥迷”的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
附: ,其中
,其中 .
.
冬奥迷 | 非冬奥迷 | 总计 | |
男 | 20 | 26 | |
女 | 14 | ||
总计 | 50 |
 列联表,并判断是否有99%的把握认为是否为“冬奥迷”与性别有关?
列联表,并判断是否有99%的把握认为是否为“冬奥迷”与性别有关?(2)现从抽取的“冬奥迷”人群中,按性别采用分层抽样的方法抽取6人,然后从这6人中随机抽取2人,记这2人中男“冬奥迷”的人数为
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.附:
 ,其中
,其中 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
您最近一年使用:0次
7 . 有甲、乙两个班级进行数学考试,若规定成绩在85分及以上为优秀,85分以下为非优秀,统计成绩后,得到如下的列联表.
已知从105个学生中随机抽取1人,其数学成绩为优秀的概率为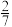 .
.
(1)请根据已知条件补全上面的列联表;
(2)依据 的独立性检验,能否认为学生的数学成绩与班级有关?
的独立性检验,能否认为学生的数学成绩与班级有关?
(3)若按下面的方法从甲班数学成绩为优秀的学生中抽取1人:把甲班数学成绩为优秀的10名学生按2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的编号(注:出现的点数之和为12时,被抽取人的编号为2),试求抽到4号或9号的概率.
单位:人 | |||
班级 | 数学成绩 | 合计 | |
优秀 | 非优秀 | ||
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 105 | ||
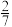 .
.(1)请根据已知条件补全上面的列联表;
(2)依据
 的独立性检验,能否认为学生的数学成绩与班级有关?
的独立性检验,能否认为学生的数学成绩与班级有关?(3)若按下面的方法从甲班数学成绩为优秀的学生中抽取1人:把甲班数学成绩为优秀的10名学生按2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的编号(注:出现的点数之和为12时,被抽取人的编号为2),试求抽到4号或9号的概率.
您最近一年使用:0次
名校
8 . 线上直播带货弥补了人们因疫情足不出户的消费需求.某直播平台抽取了该平台秀场类200个直播间,进行了一次直播销量抽样调查,其中播出时间固定的有120个,播出时间不固定的有80个.这200场直播单位时间(分钟)销量的频率分布直方图如图所示,假设该平台规定单位时间(分钟)销量在1000份及以上的为“高销量直播间”.据统计,在这200场直播中,播出时间固定且为“高销量直播间”的频率为0.35.

(1)补全 列联表,并根据表中数据判断是否有99.5%的把握认为单位时间(分钟)销量与播出时间是否固定有关系;
列联表,并根据表中数据判断是否有99.5%的把握认为单位时间(分钟)销量与播出时间是否固定有关系;
(2)将上述调查所得的频率视为概率,从该平台秀场类直播中随机抽取3场,记“高销量直播间”的场数为X,求X的分布列和期望;
(3)仍将上述调查所得的频率视为概率,规定“高销量直播间”奖励5颗星,“非高销量直播间”奖励3颗星.仍从该平台秀场类直播中随机抽取3场,记他们所获星数为Y,求Y的期望.
附: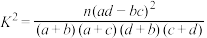 .
.

(1)补全
 列联表,并根据表中数据判断是否有99.5%的把握认为单位时间(分钟)销量与播出时间是否固定有关系;
列联表,并根据表中数据判断是否有99.5%的把握认为单位时间(分钟)销量与播出时间是否固定有关系;播出时间固定 | 播出时间不固定 | 总计 | |
高销量直播间 | |||
非高销量直播间 | |||
总计 | 120 | 80 | 200 |
(3)仍将上述调查所得的频率视为概率,规定“高销量直播间”奖励5颗星,“非高销量直播间”奖励3颗星.仍从该平台秀场类直播中随机抽取3场,记他们所获星数为Y,求Y的期望.
附:
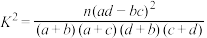 .
.
| 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
名校
9 . 2021年,福建、河北、辽宁、江苏、湖北、湖南、广东、重庆8省市将迎来“3+1+2”新高考模式.“3”指的是:语文、数学、英语,统一高考;“1”指的是:物理和历史,考生从中选一科;“2”指的是:化学、生物、地理和政治,考生从四科中选两科.为了迎接新高考,某中学调查了高一年级1500名学生的选科倾向,随机抽取了100人,统计选考科目人数如下表:
(1)补全2×2列联表,并根据表中数据判断是否有95%的把握认为“选考物理与性别有关”;
(2)将此样本的频率视为总体的概率,随机调查该校3名学生,设这3人中选考历史的人数为X,求X的分布列及数学期望.
参考公式: ,其中
,其中 .
.
参考数据:
| 选考物理 | 选考历史 | 总计 | |
| 男生 | 40 | 50 | |
| 女生 | |||
| 总计 | 30 |
(2)将此样本的频率视为总体的概率,随机调查该校3名学生,设这3人中选考历史的人数为X,求X的分布列及数学期望.
参考公式:
 ,其中
,其中 .
.参考数据:
 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2021-05-11更新
|
1240次组卷
|
9卷引用:天一大联考2021届高三阶段性测试(六)理科数学试题
名校
10 . 某社区为庆祝中国共产党成立100周年,举办一系列活动,通过调查得知其中参加文艺活动与体育活动的居民人数如下表:
(1)补全上表,并判断能否在犯错误的概率不超过0.5%的前提下认为参加活动的类型与性别有关?
(2)在参加活动的男性居民中,用分层抽样方法抽取7人,再从这7人中随机抽取3人接受采访,记抽到参加文艺活动的人数为 ,求
,求 的分布列与期望.
的分布列与期望.
附:
 ,其中
,其中 .
.
| 男性 | 女性 | 合计 | |
| 文艺活动 | 15 | 30 | |
| 体育活动 | 20 | 10 | |
| 合计 |
(2)在参加活动的男性居民中,用分层抽样方法抽取7人,再从这7人中随机抽取3人接受采访,记抽到参加文艺活动的人数为
 ,求
,求 的分布列与期望.
的分布列与期望.附:
 |  |  |  |  |  |
 |  |  |  |  |  |
 ,其中
,其中 .
.
您最近一年使用:0次
2022-06-21更新
|
377次组卷
|
2卷引用:2022届全国新高考Ⅱ卷仿真模拟试卷(一)