22-23高三上·四川·阶段练习
名校
解题方法
1 . 如图,某菜农有一块等腰三角形菜地,其中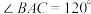 ,
,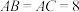 米.现将该三角形菜地分成三块,其中
米.现将该三角形菜地分成三块,其中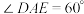 .
.

(1)若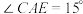 ,求
,求 的长;
的长;
(2)求 面积的最小值.
面积的最小值.
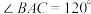 ,
,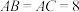 米.现将该三角形菜地分成三块,其中
米.现将该三角形菜地分成三块,其中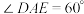 .
.
(1)若
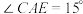 ,求
,求 的长;
的长;(2)求
 面积的最小值.
面积的最小值.
您最近一年使用:0次
2022-10-15更新
|
1043次组卷
|
7卷引用:浙江省浙北G2联盟2022-2023学年高一下学期4月期中联考数学试题
解题方法
2 . 如图1,在 中,
中, ,
, ,点D,E分别在边AB,AC上,
,点D,E分别在边AB,AC上, ,连接DC,点M,P,N分别为DE,DC,BC的中点.
,连接DC,点M,P,N分别为DE,DC,BC的中点.
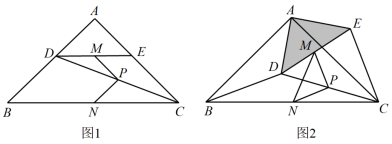
(1)观察猜想:图1中,线段PM与PN的数量关系是________,位置关系是________;
(2)探究证明:把 绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断
绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断 的形状,并说明理由;
的形状,并说明理由;
(3)拓展延伸:把 绕点A在平面内自由旋转,若
绕点A在平面内自由旋转,若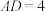 ,
, ,请直接写出
,请直接写出 面积的最大值.
面积的最大值.
 中,
中, ,
, ,点D,E分别在边AB,AC上,
,点D,E分别在边AB,AC上, ,连接DC,点M,P,N分别为DE,DC,BC的中点.
,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想:图1中,线段PM与PN的数量关系是________,位置关系是________;
(2)探究证明:把
 绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断
绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断 的形状,并说明理由;
的形状,并说明理由;(3)拓展延伸:把
 绕点A在平面内自由旋转,若
绕点A在平面内自由旋转,若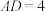 ,
, ,请直接写出
,请直接写出 面积的最大值.
面积的最大值.
您最近一年使用:0次
3 . 为了美化城市空间,拓展市民公共活动场所,某市拟把一块直角三角形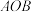 空地修建成一个“口袋公园”(指规模很小的城市户外空间).建造时,须在公园内留出一块绿地(
空地修建成一个“口袋公园”(指规模很小的城市户外空间).建造时,须在公园内留出一块绿地(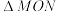 区域),
区域),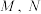 在
在 上,
上,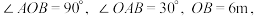 其余区域为休闲区.
其余区域为休闲区.

(1)当图中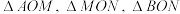 三个区域的面积相等时,求绿地区域
三个区域的面积相等时,求绿地区域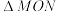 的周长;
的周长;
(2)若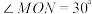 ,为使休闲区尽量大,设
,为使休闲区尽量大,设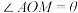 ,问
,问 为何值时,绿地区域
为何值时,绿地区域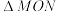 的面积最小?最小面积是多少?
的面积最小?最小面积是多少?
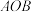 空地修建成一个“口袋公园”(指规模很小的城市户外空间).建造时,须在公园内留出一块绿地(
空地修建成一个“口袋公园”(指规模很小的城市户外空间).建造时,须在公园内留出一块绿地(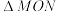 区域),
区域),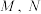 在
在 上,
上,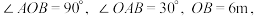 其余区域为休闲区.
其余区域为休闲区.
(1)当图中
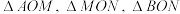 三个区域的面积相等时,求绿地区域
三个区域的面积相等时,求绿地区域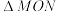 的周长;
的周长;(2)若
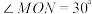 ,为使休闲区尽量大,设
,为使休闲区尽量大,设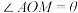 ,问
,问 为何值时,绿地区域
为何值时,绿地区域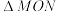 的面积最小?最小面积是多少?
的面积最小?最小面积是多少?
您最近一年使用:0次
名校
解题方法
4 . 北京2022年冬奥会将于2022年2月4日在北京和张家口开幕,运动员休息区本着环保、舒适、温馨这一出发点,进行精心设计.如图,道路 长为
长为 百米,现在
百米,现在 的同一侧设计四边形
的同一侧设计四边形 ,
, ,
, 在以
在以 为直径的半圆上设
为直径的半圆上设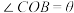 ,(
,( 为圆心).
为圆心).

(1)若在四边形 内种植花卉,且
内种植花卉,且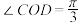 ,当
,当 为何值时,花卉种植面积最大?
为何值时,花卉种植面积最大?
(2)若为了景观错落有致,沿着 ,
, 和
和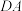 设置景观花带,且
设置景观花带,且 ,则当
,则当 为何值时,景观花带总长
为何值时,景观花带总长 最长?并求
最长?并求 的最大值.
的最大值.
 长为
长为 百米,现在
百米,现在 的同一侧设计四边形
的同一侧设计四边形 ,
, ,
, 在以
在以 为直径的半圆上设
为直径的半圆上设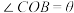 ,(
,( 为圆心).
为圆心).
(1)若在四边形
 内种植花卉,且
内种植花卉,且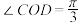 ,当
,当 为何值时,花卉种植面积最大?
为何值时,花卉种植面积最大?(2)若为了景观错落有致,沿着
 ,
, 和
和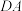 设置景观花带,且
设置景观花带,且 ,则当
,则当 为何值时,景观花带总长
为何值时,景观花带总长 最长?并求
最长?并求 的最大值.
的最大值.
您最近一年使用:0次
2021-11-24更新
|
576次组卷
|
2卷引用:浙江省湖州中学2021-2022学年高一下学期第一次质量检测数学试题
20-21高一下·浙江·期末
名校
解题方法
5 . 某市需拍卖一块近似圆形的土地(如图),内接于圆的平面四边形 作为建筑用地,周边需做绿化.因地面限制,只能测量出
作为建筑用地,周边需做绿化.因地面限制,只能测量出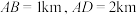 ,测角仪测得角
,测角仪测得角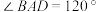 .
.
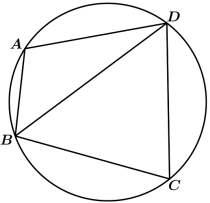
(1)求 的长;
的长;
(2)因地理条件限制, 不能变更,但点C可以调整.建筑商为利益最大化,要求在弧上设计一点C使得四边形
不能变更,但点C可以调整.建筑商为利益最大化,要求在弧上设计一点C使得四边形 面积最大,求四边形
面积最大,求四边形 面积的最大值.
面积的最大值.
 作为建筑用地,周边需做绿化.因地面限制,只能测量出
作为建筑用地,周边需做绿化.因地面限制,只能测量出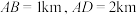 ,测角仪测得角
,测角仪测得角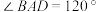 .
.
(1)求
 的长;
的长;(2)因地理条件限制,
 不能变更,但点C可以调整.建筑商为利益最大化,要求在弧上设计一点C使得四边形
不能变更,但点C可以调整.建筑商为利益最大化,要求在弧上设计一点C使得四边形 面积最大,求四边形
面积最大,求四边形 面积的最大值.
面积的最大值.
您最近一年使用:0次
2021-05-19更新
|
698次组卷
|
5卷引用:【新东方】双师265高一下
(已下线)【新东方】双师265高一下(已下线)【新东方】高中数学20210527-027【2021】【高一下】浙江省“七彩阳光”新高考研究联盟2020-2021学年高一下学期期中联考数学试题上海市金山中学2020-2021学年高一下学期期末数学试题上海市华东师范大学第三附属中学2021-2022学年高一下学期期末数学试题



