名校
解题方法
1 . 2023年12月28日工业和信息化部等八部门发布了关于加快传统制造业转型升级的指导意见,红星机械厂积极响应决定投资生产 产品.经过市场调研,生产
产品.经过市场调研,生产 产品的固定成本为300万元,每生产
产品的固定成本为300万元,每生产 万件,需可变成本
万件,需可变成本 万元,当产量不足50万件时,
万元,当产量不足50万件时, ;当产量不小于50万件时,
;当产量不小于50万件时, .每件
.每件 产品的售价为200元,通过市场分析,生产的
产品的售价为200元,通过市场分析,生产的 产品可以全部销售完.
产品可以全部销售完.
(1)求利润函数的解析式;
(2)求利润函数的最大值.
 产品.经过市场调研,生产
产品.经过市场调研,生产 产品的固定成本为300万元,每生产
产品的固定成本为300万元,每生产 万件,需可变成本
万件,需可变成本 万元,当产量不足50万件时,
万元,当产量不足50万件时, ;当产量不小于50万件时,
;当产量不小于50万件时, .每件
.每件 产品的售价为200元,通过市场分析,生产的
产品的售价为200元,通过市场分析,生产的 产品可以全部销售完.
产品可以全部销售完.(1)求利润函数的解析式;
(2)求利润函数的最大值.
您最近一年使用:0次
2024-03-29更新
|
463次组卷
|
5卷引用: 广西桂林市田家炳中学2023-2024学年高二下学期期中测试数学试题
广西桂林市田家炳中学2023-2024学年高二下学期期中测试数学试题河北省张家口市张北县第一中学等校2023-2024学年高二下学期3月阶段测试数学试卷(A)(已下线)模块五 专题1 全真基础模拟1(苏教版高二期中研习)广东省肇庆市封开县江口中学2023-2024学年高二下学期5月期中考试数学试题(已下线)广东省清远市2023-2024学年高二下学期期中联合考试数学试题变式题16-19
解题方法
2 . 2014年,几个生产袋装螺蛳粉的小作坊在柳州悄然出现,打破了长期以来螺蛳粉只能“现煮堂食”的局面,政府通过引导,让相关产业逐步走向标准化,2018年8月20日,“柳州螺蛳粉”获得国家地理标志商标,2020年新冠肺炎疫情期间,柳州螺蛳粉逆势而上,成为全国热销产品,迅速走红.2022年,柳州螺蛳粉全产业链销售收入600.7亿元、增长19.8%,其中预包装柳州螺蛳粉销售收入182亿元、增长19.6%,年寄递量达到1.1亿件,今年某平台网红委托某工厂代加工袋装螺蛳粉,生产该款产品每月固定成本为4万元,每生产 万袋,需另投入成本
万袋,需另投入成本 万元.当产量不足6万袋时,
万元.当产量不足6万袋时,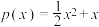 ;当产量不小于6万袋时,
;当产量不小于6万袋时,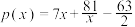 .若该产品工厂的供货价为6元/袋,根据平台网流量,该款产品可以全部销售完.
.若该产品工厂的供货价为6元/袋,根据平台网流量,该款产品可以全部销售完.
(1)求工厂生产该款产品每月所获利润 (万元)关于产量
(万元)关于产量 (万袋)的函数关系式;
(万袋)的函数关系式;
(2)当月产量为多少万袋时,工厂生产该款产品每月所获利润最大,为多少万元?
 万袋,需另投入成本
万袋,需另投入成本 万元.当产量不足6万袋时,
万元.当产量不足6万袋时,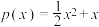 ;当产量不小于6万袋时,
;当产量不小于6万袋时,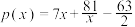 .若该产品工厂的供货价为6元/袋,根据平台网流量,该款产品可以全部销售完.
.若该产品工厂的供货价为6元/袋,根据平台网流量,该款产品可以全部销售完.(1)求工厂生产该款产品每月所获利润
 (万元)关于产量
(万元)关于产量 (万袋)的函数关系式;
(万袋)的函数关系式;(2)当月产量为多少万袋时,工厂生产该款产品每月所获利润最大,为多少万元?
您最近一年使用:0次
12-13高二下·江苏宿迁·期中
名校
解题方法
3 . 小王大学毕业后,决定利用所学专业进行自主创业.经过市场调查,生产某小型电子产品需投入年固定成本为2万元,每生产 万件,需另投入流动成本为
万件,需另投入流动成本为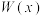 万元,在年产量不足8万件时,
万元,在年产量不足8万件时, (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,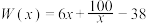 (万元),每件产品售价为5元.通过市场分析,小王生产的商品能当年全部售完.
(万元),每件产品售价为5元.通过市场分析,小王生产的商品能当年全部售完.
(1)写出年利润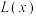 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式;
(万件)的函数解析式;
(注:年利润=年销售收入-固定成本-流动成本)
(2)年产量为多少万件时,小王在这一商品的生产中所获利润最大?最大利润是多少?
 万件,需另投入流动成本为
万件,需另投入流动成本为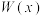 万元,在年产量不足8万件时,
万元,在年产量不足8万件时, (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,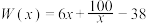 (万元),每件产品售价为5元.通过市场分析,小王生产的商品能当年全部售完.
(万元),每件产品售价为5元.通过市场分析,小王生产的商品能当年全部售完.(1)写出年利润
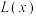 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式;
(万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(2)年产量为多少万件时,小王在这一商品的生产中所获利润最大?最大利润是多少?
您最近一年使用:0次
2023-02-01更新
|
360次组卷
|
28卷引用:广西桂林市中山中学2021-2022学年高二上学期期中质量检测数学(理)试题
广西桂林市中山中学2021-2022学年高二上学期期中质量检测数学(理)试题(已下线)2012-2013学年江苏省沭阳县高二下学期期中调研测试文科数学试卷(已下线)2012-2013学年江苏省沭阳县高二下学期期中调研测试理科数学试卷河北省衡水市第十三中学2019-2020学年高一下学期调研数学试题(已下线)专题2.9 函数模型及其应用(精讲)-2021年高考数学(理)一轮复习学与练(已下线)专题2.9 函数模型及其应用(精讲)-2021年高考数学(文)一轮复习学与练(已下线)3.3+函数的应用(一)+3.4+数学建模活动:决定苹果的最佳出售时间点(同步学案,)-新教材2020-2021学年高一数学同步备课(人教B版必修第一册)湖南省常德市淮阳中学2020-2021学年高一上学期期中数学试题山东省东营市胜利一中2020-2021学年度高一第一学期期中考试数学试题(已下线)第8章+函数应用(能力提升)-2020-2021学年高一数学单元测试定心卷(苏教版2019必修第一册)安徽省淮北市树人高级中学2020-2021学年高一上学期期末数学试题江苏省无锡市江阴市成化高级中学2020-2021学年高一上学期12月月考数学试题安徽省阜阳市耀云中学2020-2021学年高二上学期期中数学试题福建省厦门市双十中学2021-2022学年高一上学期数学返校摸底考试试题河北省博野中学2021-2022学年高一上学期10月月考数学试题江苏省无锡市第一中学2021-2022学年高一艺术班上学期期末数学试题(已下线)第18讲 函数模型及其运用-备战2023年高考数学一轮复习考点帮(新高考专用)陕西省咸阳市高新一中2022-2023学年高一上学期期中数学试题(A卷)四川省泸州市泸县第一中学2022-2023学年高一上学期期中考试数学试题辽宁省本溪市第一中学2022-2023学年高一上学期期末数学试题河南省洛阳市伊川县实验高中2021-2022学年高一上学期第二次月考数学试题四川省泸州市泸县第四中学2022-2023学年高一下学期开学考试数学试题重庆市永川北山中学校2022-2023学年高一上学期期末联考数学试题河南省通许县丽星高级中学2022-2023学年高一上学期第二次月考数学试题2.1.3基本不等式的应用四川省泸县第一中学2023-2024学年高一上学期10月月考数学试题北京市大峪中学2023-2024学年高一上学期期中考试数学试题(已下线)8.2 函数与数学模型(六大题型)-【帮课堂】(苏教版2019必修第一册)
名校
解题方法
4 . 2022年某企业整合资金投入研发高科技产品,并面向全球发布了首批17项科技创新重大技术需求榜单,吸引清华大学、北京大学等60余家高校院所参与,实现企业创新需求与国内知名科技创新团队的精准对接,最终该公司产品研发部决定将某项高新技术应用到某高科技产品的生产中,计划该技术全年需投入固定成本6200万元,每生产 千件该产品,需另投入成本
千件该产品,需另投入成本 万元,且
万元,且 ,假设该产品对外销售单价定为每件0.9万元,且全年内生产的该产品当年能全部售完.
,假设该产品对外销售单价定为每件0.9万元,且全年内生产的该产品当年能全部售完.
(1)求出全年的利润 万元关于年产量
万元关于年产量 千件的函数关系式;
千件的函数关系式;
(2)试求该企业全年产量为多少千件时,所获利润最大,并求出最大利润.
 千件该产品,需另投入成本
千件该产品,需另投入成本 万元,且
万元,且 ,假设该产品对外销售单价定为每件0.9万元,且全年内生产的该产品当年能全部售完.
,假设该产品对外销售单价定为每件0.9万元,且全年内生产的该产品当年能全部售完.(1)求出全年的利润
 万元关于年产量
万元关于年产量 千件的函数关系式;
千件的函数关系式;(2)试求该企业全年产量为多少千件时,所获利润最大,并求出最大利润.
您最近一年使用:0次
2023-01-14更新
|
867次组卷
|
8卷引用:广西百色市平果市铝城中学2023-2024学年高一上学期期末数学解答题专项训练(二)
广西百色市平果市铝城中学2023-2024学年高一上学期期末数学解答题专项训练(二)湖北省武汉市重点中学4G+联合体2022-2023学年高一上学期期末联考数学试题湖北省武汉市第二中学2023-2024学年高一上学期第一次月考数学试题湖北省武汉市第二中学2023-2024学年高一上学期10月月考数学试题黑龙江省大庆市大庆外国语学校2023-2024学年高一上学期期中数学试题安徽省黄山市黄山学校2022-2023学年高一上学期12月月考模拟数学试题河北省石家庄市河北师大附中2023-2024学年高一上学期第三次月考(12月)数学试题山东省临沂第一中学2023-2024学年高一上学期期末模拟数学试题
名校
5 . 某厂家生产医用防护用品需投入年固定成本100万元,另生产 万件时,还需要投入流动成本
万件时,还需要投入流动成本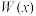 万元,在年产量不足
万元,在年产量不足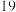 万件时,
万件时, (万元),在年产量大于或等于19万件时,
(万元),在年产量大于或等于19万件时, (万元),每万件产品售价为25(万元),通过市场分析,该厂家生产的医用防护用品当年能全部售完.
(万元),每万件产品售价为25(万元),通过市场分析,该厂家生产的医用防护用品当年能全部售完.
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(2)年产量为多少万件时,该生产厂家在这一商品的生产中获得利润最大?最大利润是多少?
 万件时,还需要投入流动成本
万件时,还需要投入流动成本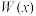 万元,在年产量不足
万元,在年产量不足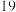 万件时,
万件时, (万元),在年产量大于或等于19万件时,
(万元),在年产量大于或等于19万件时, (万元),每万件产品售价为25(万元),通过市场分析,该厂家生产的医用防护用品当年能全部售完.
(万元),每万件产品售价为25(万元),通过市场分析,该厂家生产的医用防护用品当年能全部售完.(1)写出年利润
 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)(2)年产量为多少万件时,该生产厂家在这一商品的生产中获得利润最大?最大利润是多少?
您最近一年使用:0次
2021-11-12更新
|
621次组卷
|
5卷引用:广西壮族自治区南宁高新技术产业开发区桂鼎学校2022-2023学年高一上学期11月期中数学试题
名校
6 . 新冠肺炎是近百年来人类遭遇的影响范围最广的全球性大流行病,2020上半年我国疫情严重,在党的正确领导下,疫情得到有效控制,为了发展经济,国家鼓励复工复产,某手机品牌公司响应国家号召投入生产某款手机,前期投入成本40万元,每生产1万部还需另投入16万元.设该公司一年内共生产该款手机x万部并全部销售完,每万部的销售收入为 万元,且满足关系式
万元,且满足关系式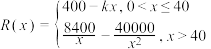 ,已知该公司一年内共生产该款手机2万部并全部销售完时,年利润为704万元.
,已知该公司一年内共生产该款手机2万部并全部销售完时,年利润为704万元.
(1)写出年利润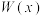 (万元)关于年产量x(万部)的函数解析式;
(万元)关于年产量x(万部)的函数解析式;
(2)当年产量为多少时,公司在该款手机的生产中所获得的利润最大?并求出最大利润.
 万元,且满足关系式
万元,且满足关系式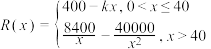 ,已知该公司一年内共生产该款手机2万部并全部销售完时,年利润为704万元.
,已知该公司一年内共生产该款手机2万部并全部销售完时,年利润为704万元.(1)写出年利润
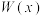 (万元)关于年产量x(万部)的函数解析式;
(万元)关于年产量x(万部)的函数解析式;(2)当年产量为多少时,公司在该款手机的生产中所获得的利润最大?并求出最大利润.
您最近一年使用:0次
2022-01-08更新
|
316次组卷
|
3卷引用:广西百色市平果市铝城中学2023-2024学年高一上学期期末数学解答题专项训练(一)
名校
7 . 新冠肺炎疫情造成医用防护服短缺,某地政府决定为防护服生产企业 公司扩大生产提供
公司扩大生产提供 (
(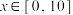 )(万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服,
)(万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服, 公司在收到政府
公司在收到政府 (万元)补贴后,防护服产量将增加到
(万元)补贴后,防护服产量将增加到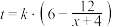 (万件),其中
(万件),其中 为工厂工人的复工率(
为工厂工人的复工率(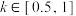 ),
), 公司生产
公司生产 万件防护服还需投入成本
万件防护服还需投入成本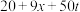 (万元).
(万元).
(1)将 公司生产防护服的利润
公司生产防护服的利润 (万元)表示为补贴
(万元)表示为补贴 (万元)的函数(政府补贴
(万元)的函数(政府补贴 万元计入公司收入);
万元计入公司收入);
(2)当复工率 时,政府补贴多少万元才能使
时,政府补贴多少万元才能使 公司的防护服利润达到最大?并求出最大值.
公司的防护服利润达到最大?并求出最大值.
 公司扩大生产提供
公司扩大生产提供 (
(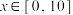 )(万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服,
)(万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服, 公司在收到政府
公司在收到政府 (万元)补贴后,防护服产量将增加到
(万元)补贴后,防护服产量将增加到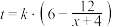 (万件),其中
(万件),其中 为工厂工人的复工率(
为工厂工人的复工率(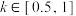 ),
), 公司生产
公司生产 万件防护服还需投入成本
万件防护服还需投入成本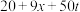 (万元).
(万元).(1)将
 公司生产防护服的利润
公司生产防护服的利润 (万元)表示为补贴
(万元)表示为补贴 (万元)的函数(政府补贴
(万元)的函数(政府补贴 万元计入公司收入);
万元计入公司收入);(2)当复工率
 时,政府补贴多少万元才能使
时,政府补贴多少万元才能使 公司的防护服利润达到最大?并求出最大值.
公司的防护服利润达到最大?并求出最大值.
您最近一年使用:0次
2021-11-08更新
|
1736次组卷
|
10卷引用:广西壮族自治区钦州市第四中学2023届高三上学期10月考试数学(?文?)试题
广西壮族自治区钦州市第四中学2023届高三上学期10月考试数学(?文?)试题湖南省长沙市第一中学2021-2022学年高一上学期期中数学试题浙江省金华市曙光学校2021-2022学年高一上学期期中数学试题江西省新余市2021-2022学年高一上学期期末数学试题山西省孝义市2021-2022学年高一上学期期末数学试题黑龙江省大庆市大庆实验中学2021-2022学年高一上学期期中数学试题江苏省连云港市2022-2023学年高一上学期期末调研数学试题(4)黑龙江省齐齐哈尔市第八中学校2022-2023学年高一上学期期末数学试题(已下线)第三章 函数的概念与性质(3)-速记·巧练(人教A版2019必修第一册)湖南省长沙市宁乡市2023-2024学年高一上学期期末考试数学试题
名校
8 . 2020年春节前后,一场突如其来的新冠肺炎疫情在武汉出现并很快地传染开来(已有证据表明2019年10月、11月国外已经存在新冠肺炎病毒),对人类生命形成巨大危害.在中共中央、国务院强有力的组织领导下,全国人民万众一心抗击、防控新冠肺炎,疫情早在3月底已经得到了非常好的控制(累计病亡人数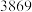 人),然而国外因国家体制、思想观念的不同,防控不力,新冠肺炎疫情越来越严重.疫情期间造成医用防护用品短缺,某厂家生产医用防护用品需投入年固定成本为
人),然而国外因国家体制、思想观念的不同,防控不力,新冠肺炎疫情越来越严重.疫情期间造成医用防护用品短缺,某厂家生产医用防护用品需投入年固定成本为 万元,每生产
万元,每生产 万件,需另投入成本为
万件,需另投入成本为 .当年产量不足
.当年产量不足 万件时,
万件时,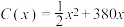 (万元);当年产量不小于
(万元);当年产量不小于 万件时,
万件时, (万元).通过市场分析,若每件售价为
(万元).通过市场分析,若每件售价为 元时,该厂年内生产的商品能全部售完.(利润
元时,该厂年内生产的商品能全部售完.(利润 销售收入
销售收入 总成本)
总成本)
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式;
(万件)的函数解析式;
(2)年产量为多少万件时,该厂在这一商品的生产中所获利润最大?并求出利润的最大值.
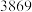 人),然而国外因国家体制、思想观念的不同,防控不力,新冠肺炎疫情越来越严重.疫情期间造成医用防护用品短缺,某厂家生产医用防护用品需投入年固定成本为
人),然而国外因国家体制、思想观念的不同,防控不力,新冠肺炎疫情越来越严重.疫情期间造成医用防护用品短缺,某厂家生产医用防护用品需投入年固定成本为 万元,每生产
万元,每生产 万件,需另投入成本为
万件,需另投入成本为 .当年产量不足
.当年产量不足 万件时,
万件时,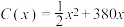 (万元);当年产量不小于
(万元);当年产量不小于 万件时,
万件时, (万元).通过市场分析,若每件售价为
(万元).通过市场分析,若每件售价为 元时,该厂年内生产的商品能全部售完.(利润
元时,该厂年内生产的商品能全部售完.(利润 销售收入
销售收入 总成本)
总成本)(1)写出年利润
 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式;
(万件)的函数解析式;(2)年产量为多少万件时,该厂在这一商品的生产中所获利润最大?并求出利润的最大值.
您最近一年使用:0次
2021-10-18更新
|
1871次组卷
|
12卷引用:广西浦北县第二中学2021-2022学年高一下学期期末模拟考试数学试题1
广西浦北县第二中学2021-2022学年高一下学期期末模拟考试数学试题1河南省新郑市2021-2022学年高一上学期第一次阶段性检测数学试题江西省赣州市赣县第三中学2022届高三上学期期中适应考试数学(理)试题辽宁省沈阳市第二中学2021-2022学年高一上学期期中数学试题辽宁省实验中学2021-2022学年高一上学期期中数学试题云南省昆明市第八中学2021-2022学年高一上学期期中考试数学试题广东省惠州市第一中学2021-2022学年高一上学期第二次阶段考试(期中)数学试题河北省邯郸市大名县第一中学2021-2022学年高一上学期第二次月考数学试题甘肃省会宁县第一中学2021-2022学年高一上学期期末考试数学试题安徽省皖西地区2021-2022学年高一下学期期中大联考数学试题湖南省常德市鼎城区第一中学2022-2023学年高一实验班上学期12月月考数学试题黑龙江省鹤岗市第一中学2022-2023学年高一上学期期中数学试题
名校
解题方法
9 . 为了振兴乡村,打好扶贫攻坚战,某企业应当地政府号召,在其扶贫基地建厂,利用当地原材料优势生产某种产品,已知年固定成本为50万元,年变动成本 (万元)与产品产量
(万元)与产品产量 (万件)的关系为
(万件)的关系为 ,产品售价为10.5万元/万件,该企业利用其产业链优势,可将该厂产品全部收购
,产品售价为10.5万元/万件,该企业利用其产业链优势,可将该厂产品全部收购
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式;
(万件)的函数解析式;
(2)当年产量为多少时,该厂年利润最大?最大利润为多少?
 (万元)与产品产量
(万元)与产品产量 (万件)的关系为
(万件)的关系为 ,产品售价为10.5万元/万件,该企业利用其产业链优势,可将该厂产品全部收购
,产品售价为10.5万元/万件,该企业利用其产业链优势,可将该厂产品全部收购(1)写出年利润
 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式;
(万件)的函数解析式;(2)当年产量为多少时,该厂年利润最大?最大利润为多少?
您最近一年使用:0次
2021-01-02更新
|
1002次组卷
|
5卷引用:广西桂林市第十八中学2022-2023学年高一上学期期中考试数学试题
名校
解题方法
10 . 佩戴口罩能起到一定预防新冠肺炎的作用,某科技企业为了满足口罩的需求,决定开发生产口罩的新机器.生产这种机器的月固定成本为 万元,每生产
万元,每生产 台,另需投入成本
台,另需投入成本 (万元),当月产量不足70台时,
(万元),当月产量不足70台时,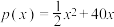 (万元);当月产量不小于70台时,
(万元);当月产量不小于70台时, (万元).若每台机器售价
(万元).若每台机器售价 万元,且该机器能全部卖完.
万元,且该机器能全部卖完.
(1)求月利润 (万元)关于月产量
(万元)关于月产量 (台)的函数关系式;
(台)的函数关系式;
(2)月产量为多少台时,该企业能获得最大月利润?并求出其利润.
 万元,每生产
万元,每生产 台,另需投入成本
台,另需投入成本 (万元),当月产量不足70台时,
(万元),当月产量不足70台时,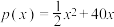 (万元);当月产量不小于70台时,
(万元);当月产量不小于70台时, (万元).若每台机器售价
(万元).若每台机器售价 万元,且该机器能全部卖完.
万元,且该机器能全部卖完.(1)求月利润
 (万元)关于月产量
(万元)关于月产量 (台)的函数关系式;
(台)的函数关系式;(2)月产量为多少台时,该企业能获得最大月利润?并求出其利润.
您最近一年使用:0次
2020-10-18更新
|
3323次组卷
|
38卷引用:广西南宁市2022-2023学年高一下学期教学质量调研数学试题
广西南宁市2022-2023学年高一下学期教学质量调研数学试题广西壮族自治区百色市德保县2023-2024学年高一上学期期中数学试题河南省平顶山市2020-2021学年高三10月阶段测试数学(文)试题河南省平顶山市2020-2021学年高三10月阶段测试数学(理)试题河南省郑州外国语学校2020-2021学年第一学期高二期中数学(文科)考试试题安徽省合肥市第一中学2020-2021学年高一上学期第二次段考数学试题安徽省合肥市第八中学2020-2021学年高一上学期期中数学试题福建省福清西山学校高中部2021届高三上学期期中考试数学试题福建省福州市八县(市)协作校2020-2021学年高一上学期期中考试数学试题安徽省蚌埠第三中学2020-2021学年高一上学期11月教学质量检测数学试题宁夏石嘴山市第三中学2020-2021学年高三上学期第二次月考数学(文科)试题河南省豫南九校2020-2021学年上学期高二数学第四次联考理科试题广东省广州市天河区2020-2021学年高一上学期期末数学试题贵州省凯里市第一中学2021-2022学年高一上学期期中考试数学试题山东省临沂市兰山区、罗庄区2021-2022学年高一上学期中考试数学试题河南省新蔡县第一高级中学2021-2022学年高二上学期11月月考数学(文科)试题山西省运城市景胜中学2021-2022学年高一上学期1月月考数学试题(已下线)专题27 应用基本不等式求最值的求解策略-学会解题之高三数学万能解题模板【2022版】福建省龙岩市上杭县第一中学2022-2023学年高一上学期10月月考数学试题山东省枣庄市第三中学2022-2023学年高一上学期10月月考数学试题山东省济宁市实验中学2022-2023学年高一上学期10月月考数学试题陕西省西安市周至县第四中学2022-2023学年高一上学期期中数学试题山东省济宁市泗水县2022-2023学年高一上学期期中考试数学试题山东省聊城颐中外国语学校2022-2023学年高一上学期期中考试数学试题河南省郑州市第一〇二高级中学2021-2022学年高一上学期期末数学试题广东省广州市西外2022-2023学年高一上学期期末数学试题广东省广州市西关外国语学校2022-2023学年高一上学期期末数学试题广东省深圳市华中师范大学龙岗附属中学2022-2023学年高一上学期期中数学试题浙江省嘉兴外国语学校2023-2024学年高一上学期期中数学试题湖南省长沙市第一中学2023-2024学年高一上学期期中考试数学试题四川省泸州市纳溪中学校等四校2023-2024学年高一上学期第一次联考数学试题四川省泸州市合江县马街中学校2023-2024学年高一上学期期中数学试题(已下线)期末真题必刷易错60题(28个考点专练)-【满分全攻略】(人教A版2019必修第一册)河北省唐山市迁安市2023-2024学年高一上学期期中考试数学试卷甘肃省武威市民勤县第一中学2023-2024学年高一上学期第二次月考数学试题河北省保定市唐县第一中学2023-2024学年高一上学期期中数学试题(已下线)高一数学第一学期期末押题密卷03卷-《考点·题型·难点》期末高效复习广东省江门市第一中学2023-2024学年高一启超学院创新班下学期3月月考数学试题



