名校
解题方法
1 . 如图,在正方体 中,
中, 分别为
分别为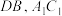 的中点,则直线
的中点,则直线 和
和 夹角的余弦值为( )
夹角的余弦值为( )
 中,
中, 分别为
分别为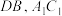 的中点,则直线
的中点,则直线 和
和 夹角的余弦值为( )
夹角的余弦值为( )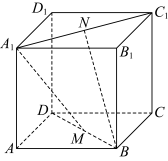
A.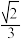 | B. | C. | D. |
您最近一年使用:0次
昨日更新
|
1557次组卷
|
11卷引用:河南省实验中学2024-2025学年高二上学期第一次月考数学试卷
河南省实验中学2024-2025学年高二上学期第一次月考数学试卷河北省承德双滦圣泉高级中学2024-2025学年高二上学期9月月考数学试卷海南省华中师范大学琼中附属中学2024-2025学年高二上学期第一次月考(10月)数学试题四川省南充高级中学2024-2025学年高三上学期10月检测数学试题四川省南充高级中学2024-2025学年高二上学期10月月考数学试题贵州省铜仁市松桃苗族自治县第三高级中学2024-2025学年高二上学期10月月考数学试题四川省南充市嘉陵第一中学2024-2025学年高二上学期第一次月考数学试题安徽省亳州市第二完全中学2024-2025学年高二上学期第一次月考数学试卷四川省眉山育英实验学校2024-2025学年高二上学期10月月考数学试卷贵州省贵阳市乌当区某校2024-2025学年高二上学期10月月考数学试题湖北省十堰市六校教学合作体2024-2025学年高二上学期10月月考数学试题
名校
解题方法
2 . 如图,平面 平面
平面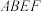 ,四边形
,四边形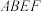 为正方形,四边形
为正方形,四边形 为菱形,
为菱形,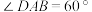 ,则直线
,则直线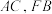 所成角的余弦值为( )
所成角的余弦值为( )
 平面
平面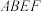 ,四边形
,四边形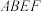 为正方形,四边形
为正方形,四边形 为菱形,
为菱形,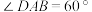 ,则直线
,则直线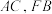 所成角的余弦值为( )
所成角的余弦值为( )
A. | B.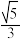 | C. | D.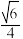 |
您最近一年使用:0次
7日内更新
|
713次组卷
|
4卷引用:江苏省无锡市第三高级中学2024-2025学年高二上学期第一次基础测试(9月)数学试卷
解题方法
3 . 已知 平面
平面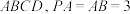 ,四边形
,四边形 为正方形.
为正方形.
(2)求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 平面
平面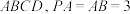 ,四边形
,四边形 为正方形.
为正方形.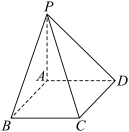

(2)求
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
7日内更新
|
798次组卷
|
2卷引用:福建省晋江市磁灶中学2022-2023学年高二上学期第一次阶段考试数学试题
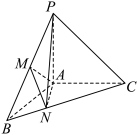
4 . 如图,在三棱锥 中,
中, 平面
平面 ,
,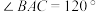 ,且
,且 ,
, 为
为 的中点,
的中点, 在
在 上,且
上,且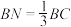 .
.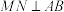 ;
;
(2)求平面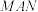 与平面
与平面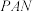 的夹角的余弦值.
的夹角的余弦值.
 中,
中, 平面
平面 ,
,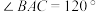 ,且
,且 ,
, 为
为 的中点,
的中点, 在
在 上,且
上,且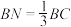 .
.
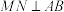 ;
;(2)求平面
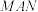 与平面
与平面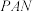 的夹角的余弦值.
的夹角的余弦值.
您最近一年使用:0次
7日内更新
|
935次组卷
|
3卷引用:河北省承德双滦圣泉高级中学2024-2025学年高二上学期9月月考数学试卷
河北省承德双滦圣泉高级中学2024-2025学年高二上学期9月月考数学试卷四川省芦山中学2023-2024学年高三上学期期中考试数学试题(已下线)核心考点2 空间向量的应用 考点讲解 (高二期中考试必考的7大核心考点)
名校
解题方法
5 . 在正方体中 ,直线
,直线 与平面
与平面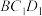 所成的角为( ).
所成的角为( ).
 ,直线
,直线 与平面
与平面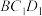 所成的角为( ).
所成的角为( ).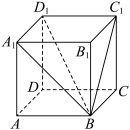
A. | B. | C. | D. |
您最近一年使用:0次
2024-10-23更新
|
768次组卷
|
4卷引用:河南省郑州市2024-2025学年高二上学期9月阶段性检测数学试题
解题方法
6 . 已知在正四棱台 中,
中,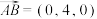 ,
,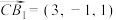 ,
, ,则异面直线
,则异面直线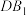 与
与 所成角的余弦值为
所成角的余弦值为__________ .
 中,
中,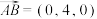 ,
,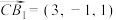 ,
, ,则异面直线
,则异面直线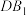 与
与 所成角的余弦值为
所成角的余弦值为
您最近一年使用:0次
2024-10-23更新
|
330次组卷
|
7卷引用:湖南省郴州市部分学校2024-2025学年高二上学期第一次月考数学试题
解题方法
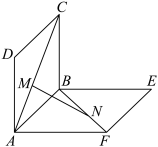
7 . 在如图所示的试验装置中,两个正方形框架 ,
,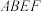 的边长都是2,且它们所在的平面互相垂直.活动弹子M,N分别在正方形对角线AC和BF上移动,且MA和NF的长度保持相等,记
的边长都是2,且它们所在的平面互相垂直.活动弹子M,N分别在正方形对角线AC和BF上移动,且MA和NF的长度保持相等,记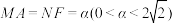 .
.
(2)当MN的长最小时,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.
 ,
,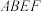 的边长都是2,且它们所在的平面互相垂直.活动弹子M,N分别在正方形对角线AC和BF上移动,且MA和NF的长度保持相等,记
的边长都是2,且它们所在的平面互相垂直.活动弹子M,N分别在正方形对角线AC和BF上移动,且MA和NF的长度保持相等,记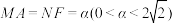 .
.
(2)当MN的长最小时,求平面
 与平面
与平面 夹角的余弦值.
夹角的余弦值.
您最近一年使用:0次
2024-10-14更新
|
84次组卷
|
2卷引用:陕西省咸阳市乾县第二中学2024-2025学年高二第二次阶段性检测数学试题
解题方法
8 . 《九章算术》是古代中国乃至东方的第一部自成体系的数学专著,书中记载了一种名为“刍甍”的五面体(如图),其中四边形 为矩形,
为矩形,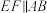 ,若
,若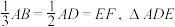 和
和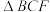 都是正三角形,
都是正三角形, 为
为 的中点,则异面直线
的中点,则异面直线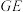 与
与 所成角的余弦值为
所成角的余弦值为______ .
 为矩形,
为矩形,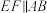 ,若
,若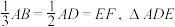 和
和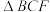 都是正三角形,
都是正三角形, 为
为 的中点,则异面直线
的中点,则异面直线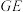 与
与 所成角的余弦值为
所成角的余弦值为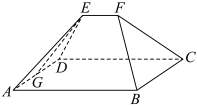
您最近一年使用:0次
2024-10-10更新
|
119次组卷
|
2卷引用:贵州省黔西南州金成实验学校2024-2025学年高二上学期第一次质量检测数学试卷
解题方法
9 . 正方体 的棱长为1,点
的棱长为1,点 在棱
在棱 上,
上, ,则平面
,则平面 与平面
与平面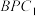 夹角的余弦值为
夹角的余弦值为______ .
 的棱长为1,点
的棱长为1,点 在棱
在棱 上,
上, ,则平面
,则平面 与平面
与平面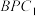 夹角的余弦值为
夹角的余弦值为
您最近一年使用:0次
2024-10-09更新
|
127次组卷
|
2卷引用:河北省承德双滦圣泉高级中学2024-2025学年高二上学期9月月考数学试卷
10 . 如图,在平行六面体 中,以顶点A为端点的三条棱长均为6,且它们彼此的夹角都是60°,下列说法中正确的是( )
中,以顶点A为端点的三条棱长均为6,且它们彼此的夹角都是60°,下列说法中正确的是( )
 中,以顶点A为端点的三条棱长均为6,且它们彼此的夹角都是60°,下列说法中正确的是( )
中,以顶点A为端点的三条棱长均为6,且它们彼此的夹角都是60°,下列说法中正确的是( )
| A.CC1⊥BD |
B.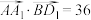 |
C.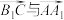 夹角是60° 夹角是60° |
D.直线 与直线 与直线 的距离是 的距离是 |
您最近一年使用:0次
2024-09-09更新
|
1792次组卷
|
7卷引用:河北省承德双滦圣泉高级中学2024-2025学年高二上学期9月月考数学试卷



